Московский государственный институт электронной техники (Технический Университет).

А.Г.Фокин

Теоретическая механика и теория поля

(конспект лекций для ЭКТ-2)

2010г.

[

[§1.] Обобщённые координаты. Понятие числа степеней свободы.

Пусть число степеней свободы равно . Для задания пространственного положения системы необходимы координаты.

– размерность пространства.

– число материальных точек.

числу координат, с помощью которых можно задать положение материальных точек.

– радиус вектор а-той точки.

Если имеются связи, т.е. ограничения, накладываемые на движение системы, причём выраженные в форме уравнений, содержащих эти координаты, то число независимых координат будет меньше на число этих связей.

- все радиус векторы.

, , где k – число связей.

Такие связи называются голономными. Если присутствует время (t) в уравнениях, то связи – нестационарные.

Для вычисления числа степеней свободы можем записать формулу:

Любые независимые переменные, полностью определяющие пространственное положение системы, называются обобщёнными координатами.

Виды координат:

Сферические .

Декартовы .

И другие.

Графическое пояснение:

Вывод данных формул элементарен по Рис.1

- i-тая компонента.

Рассмотрим пример:

Дан математический маятник (Рис.2).

- это n-мерный вектор. Здесь n=1, и уравнения связи имеют вид:

где .

- уравнение связи.

Определим число степеней свободы:

Тогда число степеней свободы равно единице.

§2. Описание эволюции системы в конфигурационном пространстве (кп).

КП – это n – мерное пространство обобщенных координат.

- радиус вектор в D-пространстве.

Реальному пространству ставим в соответствие КП

→

КП – служит для технического упрощения решения задач. Одна точка в КП изображает положение системы N материальных точек в реальном D-мерном пространстве.

Система материальных точек находится во внешнем поле, и они могут взаимодействовать между собой, поэтому движутся по каким-то траекториям. Изменение реальных координат приводит к изменению обобщенных координат. Движение реальных точек приводит к движению изображающей точки. Таким образом, эволюция системы (движение точек в реальном пространстве) описывается движением изображающей точки в КП. В результате в КП получаем траекторию.

Говоря о траектории системы, будем иметь в виду траекторию изображающей точки в КП.

Эволюция системы – это движение в реальном пространстве реальных точек по реальным траекториям.

--тая обобщённая координата, _.

Итак, имеется траектория в КП. Проведём касательный вектор - обобщенная скорость.

Чтобы описать движение системы надо знать положение точки в любой момент времени – закон движения:

Найти такую зависимость можно из закона Ньютона:

(2.1)

Решением этого уравнения будет некоторый закон движения .

Уравнение (2.1) – дифференциальное уравнение второго порядка, следовательно необходимо два начальных условия:

(2.2)

Уравнений должно быть столько, сколько степеней свободы.

Переменные вида (2.2) называются динамическими переменными – это координаты и скорости в данный момент времени. и - также динамические переменные. Зная и мы задаём механическое состояние системы в начальный момент времени.

Зная все силы, действующие на рассматриваемую систему, можно построить траекторию движения, если при этом решить уравнение движения.

§3. Принцип Гамильтона (наименьшего действия). Уравнения движения

Пусть - вариация координаты (произвольное изменение координаты в данный момент времени). Будем рассматривать бесконечно малые , следовательно, 2-я возможная траектория будет в непосредственной близости от 1-ой. Возможная траектория – траектория, которая может получиться при данных взаимодействиях. Возможных траекторий много, реальных – одна. В начальной и конечной точке траектории вариации координат равны нулю:

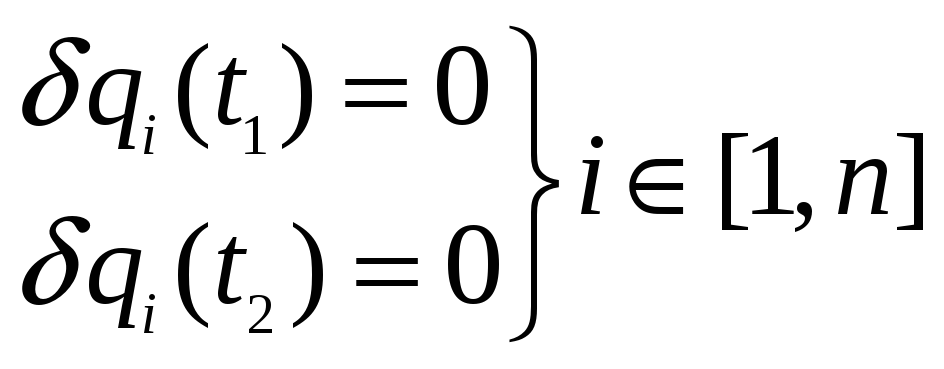
, т.е. и коммутативны:

Будем искать первую вариацию (линейную вариацию по вариацию аргумента).

Введём функционал:

- функция Лагранжа, функция динамических переменных и времени.

Принцип наименьшего действия:

Из всех возможных траекторий, между данными точками, механической системы в конфигурационном пространстве реализуется та, для которой первая вариация действия равна нулю:

Найдём :

Тогда:

Первое слагаемое в правой части данного выражения равно нулю, тогда остаётся:

Координаты независимы, вариации этих координат так же независимы. Условие независимости означает, что все коэффициенты при равны нулю. В результате получаем:

,

Мы получили уравнения движения Лагранжа. Это дифференциальные уравнения второго порядка, что бы их решить, нужны начальные условия: и . В результате получим закон движения