
§ 4. Физические приложения поверхностных интегралов
1).
Пусть
![]() — материальная поверхность с поверхностной
плотностью
— материальная поверхность с поверхностной
плотностью
![]() в точке
в точке
![]() ,
,
![]() — масса поверхности.
— масса поверхности.
2). ![]()
![]()
![]()
— статические
моменты поверхности относительно
координатных плоскостей
![]() ,
,
![]() ,
,
![]() .
.
3).
![]() ,
,
![]() ,
,
![]()
— координаты центра тяжести поверхности.
4).
![]()
-
момент инерции поверхности относительно оси
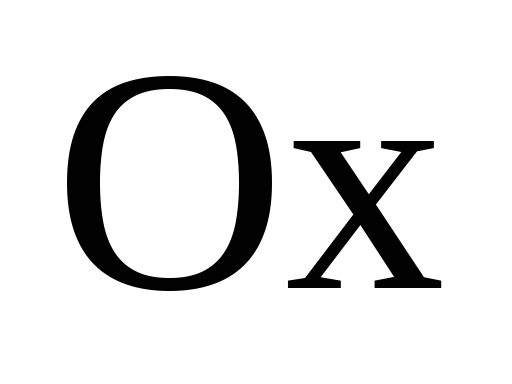 .
.
5).
![]()
— момент
инерции поверхности относительно
плоскости
![]() .
.
6).
![]()
— момент инерции поверхности относительно начала координат.
7).
![]()
![]()
![]()
— компоненты
силы притяжения
![]() материальной точки
материальной точки
![]() массы
массы
![]() материальной поверхности
материальной поверхности
![]() .
.
8).
![]() — количество (объем) жидкости, протекающей
через поверхность
— количество (объем) жидкости, протекающей
через поверхность
![]() в заданную сторону со скоростью
в заданную сторону со скоростью
![]() .
.
ПРИМЕР 12.
Вычислите момент
инерции
![]() относительно оси
относительно оси
![]() однородной сферической оболочки
однородной сферической оболочки
![]() плотности
плотности
![]() .
.
РЕШЕНИЕ:
воспользуемся формулой, аналогичной (IV,4),
![]() .
.
Запишем параметрические уравнения данной полусферы:
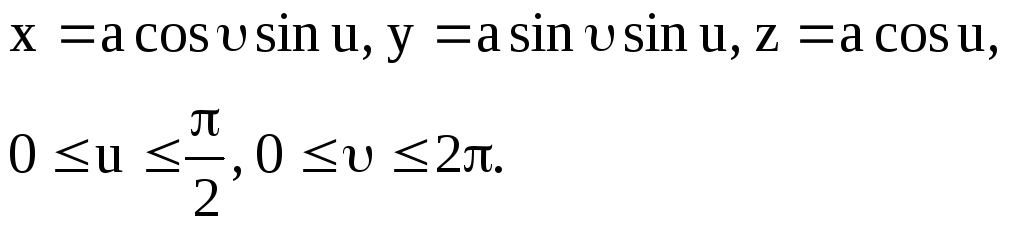
Вычислим
![]() :
:
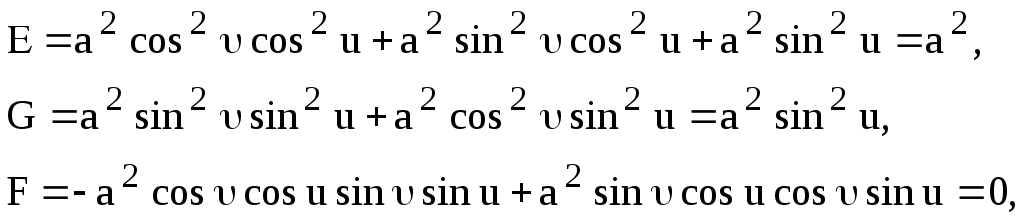
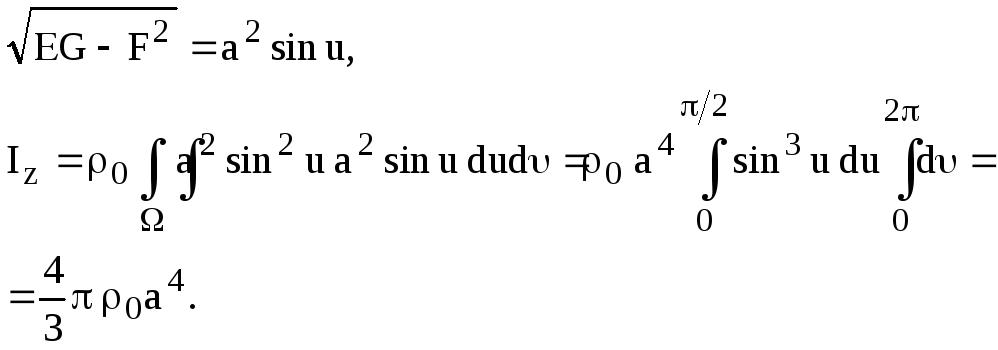
ЗАДАЧА. Заряд Q
равномерно распределен по сфере радиуса
R.
Найти напряженность электрического
поля сферы в точке A,
находящейся на расстоянии
![]() от центра сферы.
от центра сферы.
§ 5. Формулы грина, стокса, гаусса-остроградского
1). Формула Грина:
![]()
(граница L области G пробегается в положительном направлении).
2). Формула Стокса:
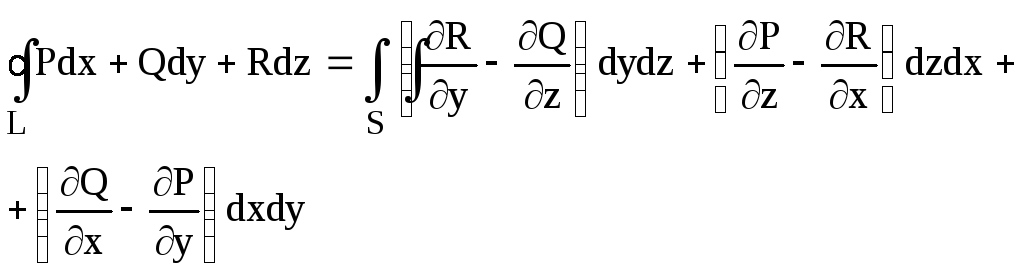
(контур L, ограничивающий поверхность S, пробегается в положительном направлении, согласованном с ориентацией поверхности).
Ротором вектора называется вектор
 .
.
Таким
образом, циркуляция вектора
![]() по замкнутому контуру L
равна потоку ротора этого вектора через
любую поверхность S,
натянутую на контур L:
по замкнутому контуру L
равна потоку ротора этого вектора через
любую поверхность S,
натянутую на контур L:
![]() .
.
3). Формула Гаусса - Остроградского:
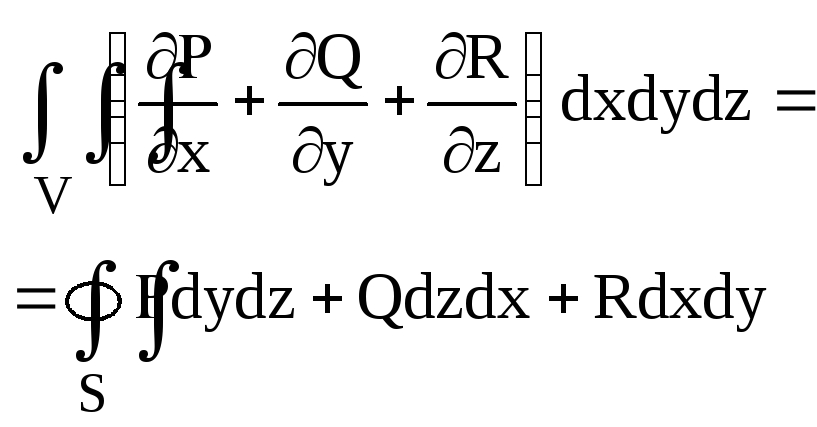
(поверхностный интеграл берется по внешней стороне поверхности S, ограничивающей область V).
Дивергенцией
вектора
![]() называется скалярная величина
называется скалярная величина
![]() .
.
Таким
образом, поток вектора
![]() через замкнутую поверхность S
равен тройному интегралу от дивергенции
вектора по области, ограниченной
поверхностью S:
через замкнутую поверхность S
равен тройному интегралу от дивергенции
вектора по области, ограниченной
поверхностью S:
![]() .
.
ПРИМЕР 13.
Вычислить
поток вектора
![]() через замкнутую поверхность
через замкнутую поверхность
![]() .
.
РЕШЕНИЕ:
по формуле Гаусса - Остроградского
![]() .
.
Вычислим интеграл, переходя к сферическим координатам
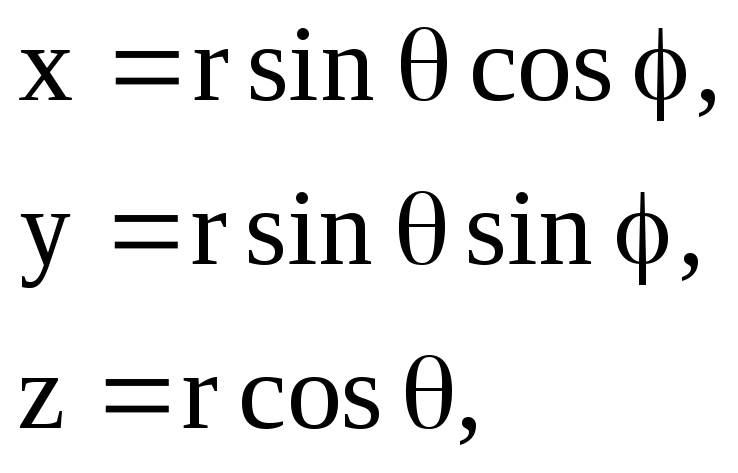
![]() .
.
Итак,
![]()
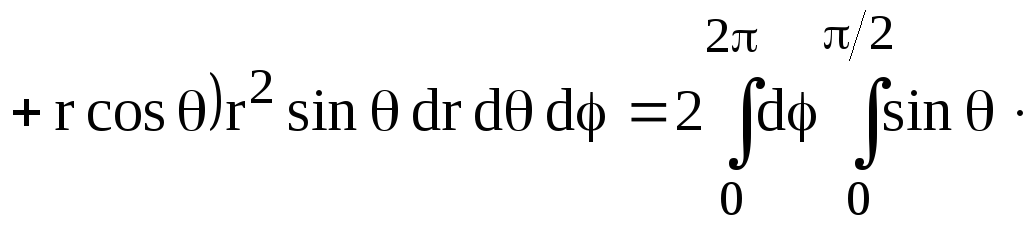
![]() .
.
ПРИМЕР 14.
Вычислить
циркуляцию вектора
![]() по контуру L:
по контуру L:
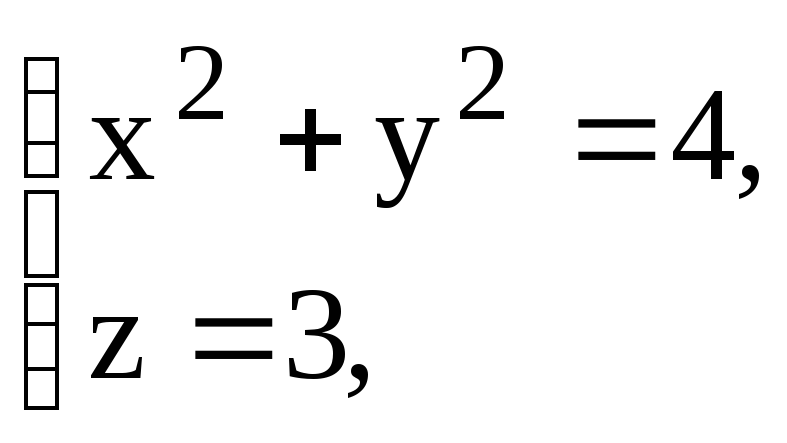
-
непосредственно, 2) по теореме Стокса.
РЕШЕНИЕ:
1).
Контур L
— окружность радиуса
![]() ,
лежащая в плоскости
,
лежащая в плоскости
![]() .
.
Параметризуем
кривую L:
![]()
![]() ,
,
Ц=![]()
![]()
2). В качестве поверхности S, натянутой на контур L, выберем круг, имеющий линию L своей границей.
![]() ,
,
Ц=![]()
![]() .
.
ПРИМЕР 15.
Вычислить циркуляцию вектора
![]()
по
окружности
![]() .
.
РЕШЕНИЕ:
циркуляция данного вектора равна
Ц=![]() .
.
Применим формулу Грина:
Ц=![]()
![]()
Перейдем
к полярным координатам:
![]() ,
,
![]()
Ц=![]()
![]() .
.
ЗАНЯТИЕ 5: 4298, 4300, 4374, 4390.
ЗАДАНИЕ 5: См. далее индивидуальные задания.
УПРАЖНЕНИЯ:
-
Используя теорему Гаусса-Остроградского, вычислить поток векторного поля
![]()
через
внешнюю сторону части поверхности
![]() ,
расположенной над плоскостью
,
расположенной над плоскостью
![]() .
.
-
Применяя формулу Грина, вычислить циркуляцию вектора
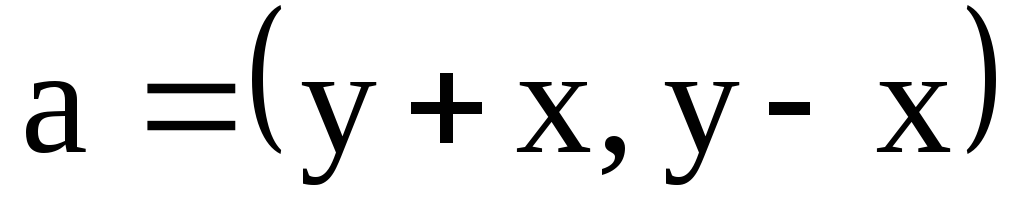 вдоль контура L:
вдоль контура L:
![]() .
.
-
Дано векторное поле скоростей точек твердого тела, вращающегося с постоянной угловой скоростью вокруг оси. Вычислить циркуляцию этого поля по окружности

непосредственно и по теореме Стокса.
