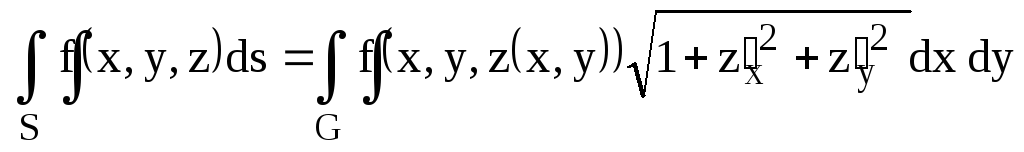Решение: масса равна

.

Значения находим по формулам (ІI.3):

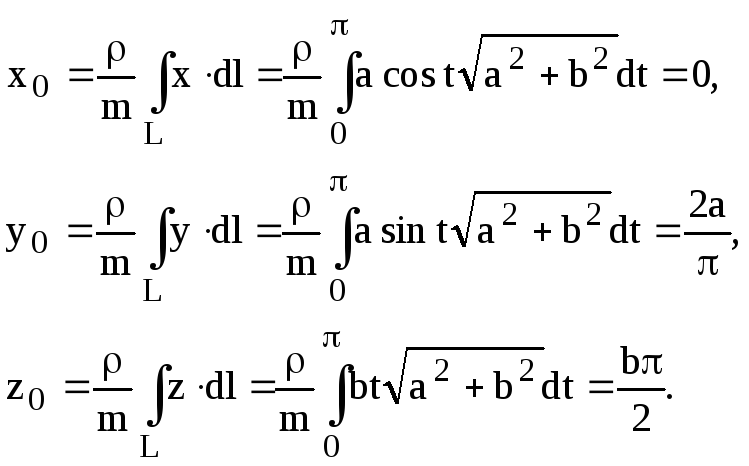
УПРАЖНЕНИЯ:

I. Найти массу материальной кривой с линейной плотностью , если:

а)

;

б) — половина дуги эллипса , для которой .

2. Найти статические моменты дуги астроиды , относительно осей координат, если линейная плотность .

3. Пусть — скорость плоского потока жидкости в точке . Вычислите количество жидкости, вытекающее за единицу времени из области

.

4. Вычислить работу силы вдоль замкнутого контура 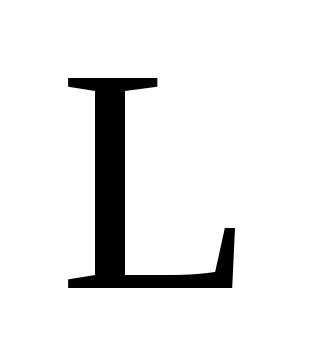в положительном направлении, если:

а) — треугольник с вершинами ,,

б) — эллипс .

5. Найти магнитную индукцию 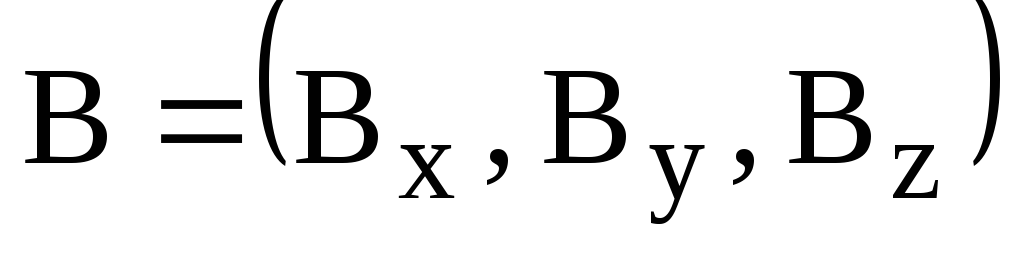магнитного поля, создаваемого током 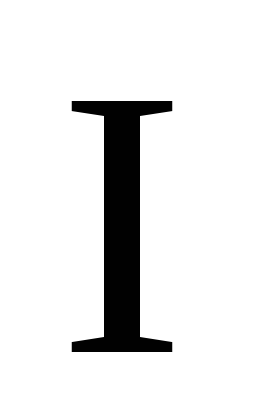, протекающим по замкнутому проводнику 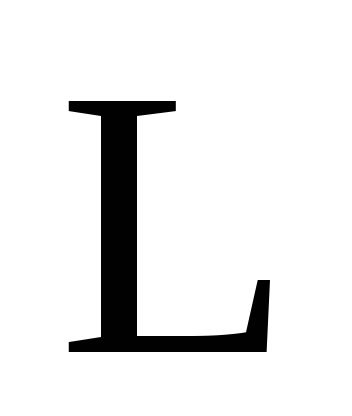в точке .

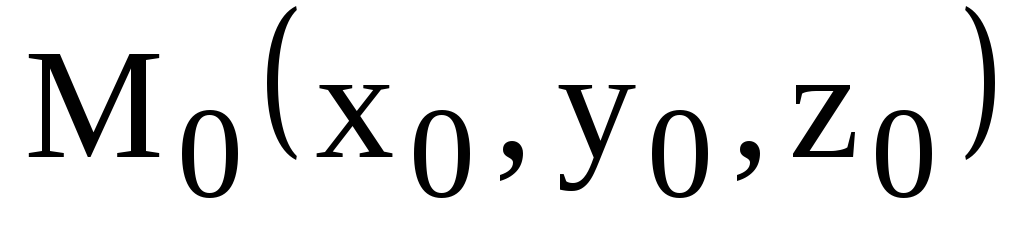§3. Поверхностные интегралы

Формулы вычисления поверхностного интеграла первого рода по поверхности :

1. 

(Поверхность задана уравнением ),

2. 

(Поверхность задана параметрически , , , ).

Здесь:

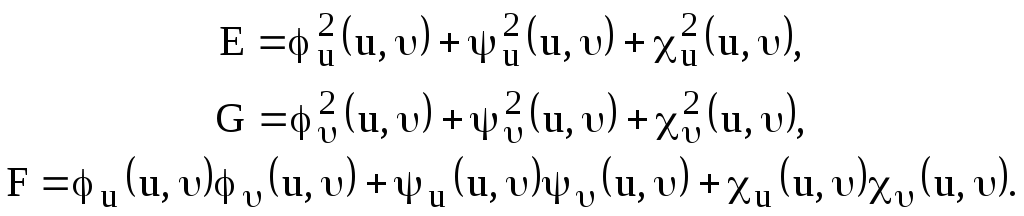
Формулы вычисления поверхностного интеграла второго рода по выбранной стороне поверхности :

3. 

,

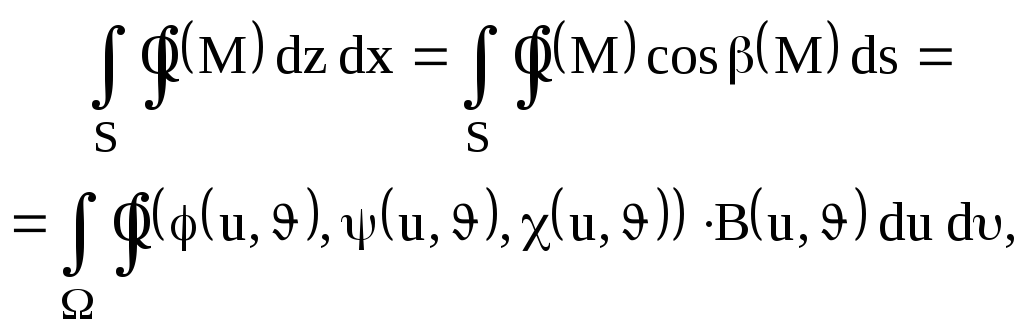
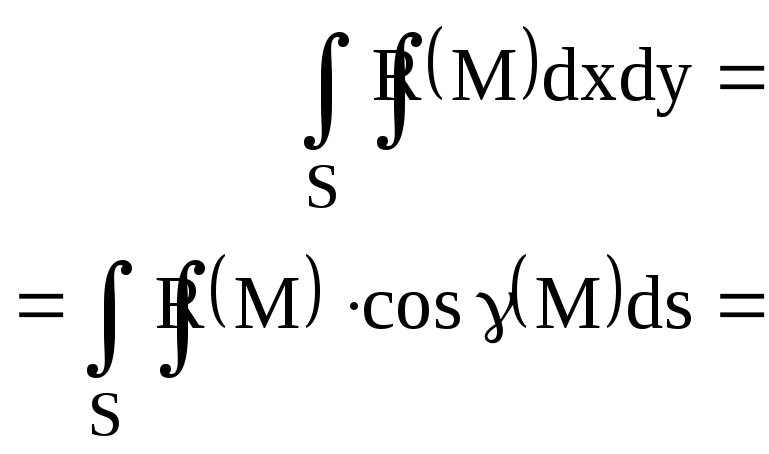
Здесь

, , .

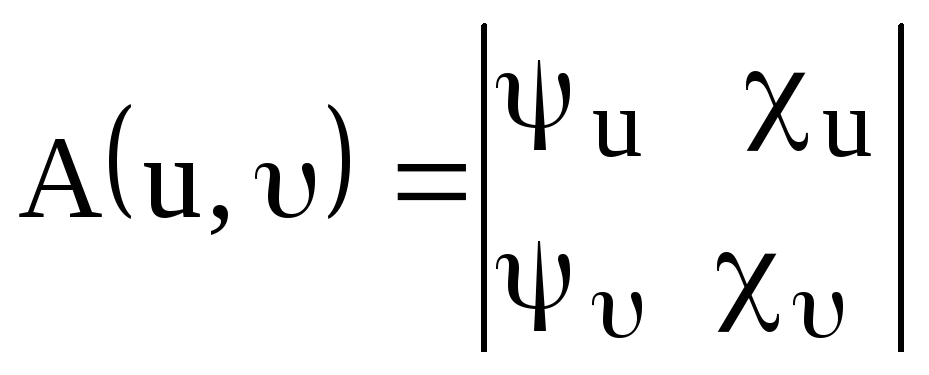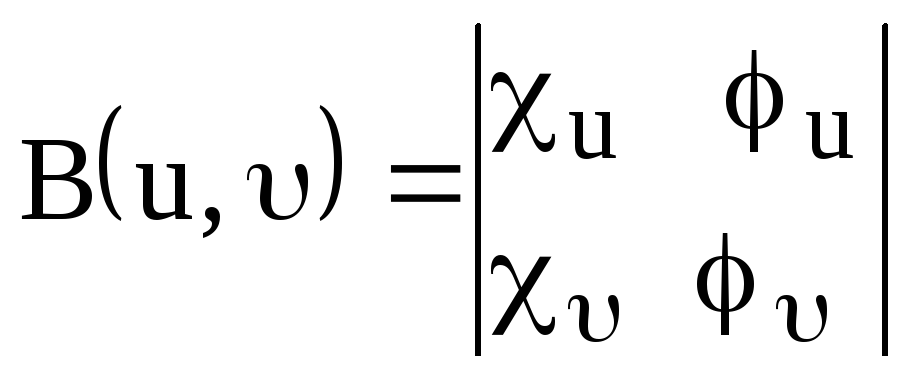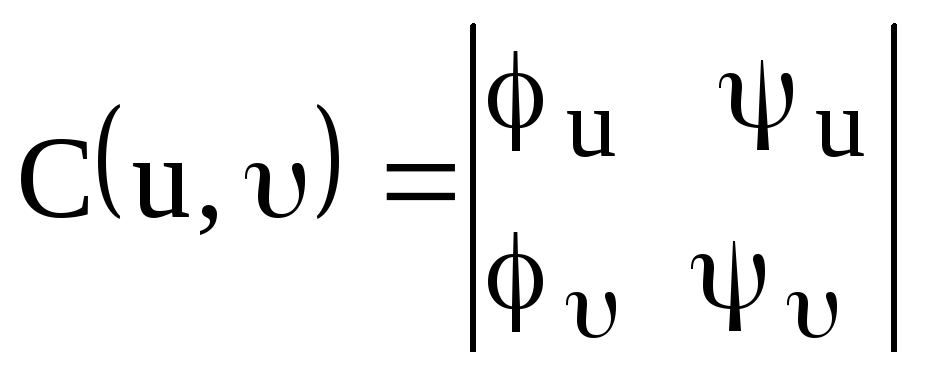4.

( рис. 2).

Аналогично получаются формулы для вычисления интегралов

, если поверхность задана, соответственно, уравнениями

:

.

Потоком векторного поля через поверхность на сторону, определяемую вектором , называется поверхностный интеграл

.

Если в системе координат

,

то

.

ПРИМЕР 7.

Вычислить поверхностный интеграл , где — граница тела (рис.3).

РЕШЕНИЕ:

интегрирование производится по

боковой поверхности и основанию конуса, в силу чего мы можем записать

,

где — боковая поверхность,

— основание. На основании , поэтому

.

На боковой поверхности , поэтому

.

В результате .

ПРИМЕР 8.

В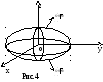ычислить поверхностный интеграл , где — эллипсоид (рис.4).

РЕШЕНИЕ:

запись означает, что интеграл вычисляется по внешней стороне эллипсоида, означает необходимость проектирования на

плоскость . Верхняя половина эллипсоида и нижняя половина проецируются в круг .

, где — верхняя половина эллипсоида, а — нижняя.

,

, где — проекции на плоскость , т.е. круг . Т.к. , а знаки интегралов противоположны, то .

П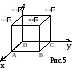РИМЕР 9.

Найти поток векторного поля на внутреннюю поверхность куба, ограниченного плоскостями

,

,

.

РЕШЕНИЕ:

,

,

т.к. площадки перпендикулярны плоскости .

Итак,

.

Аналогично,

, .

Следовательно, .

ПРИМЕР 10.

В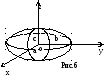ычислить по верхней стороне верхней половины эллипсоида

РЕШЕНИЕ:

так как , то по формулам (3)

(верхней стороне поверхности отвечает знак плюс в упомянутой формуле).

ПРИМЕР 11.

Если поверхность задана неявно , то нормаль к ней может быть найдена по формуле

,

т.к. вектор – градиент функции перпендикулярен к ее линиям уровня.

Так для внешней стороны поверхности параболоида , отсеченного плоскостью , имеем , и направлен в сторону возрастания . В данном случае направление градиента совпадает с направлением внешней нормали, поэтому выбирается знак ”+” и .

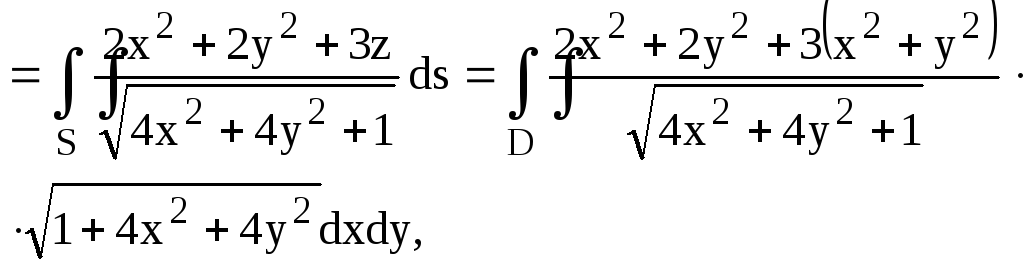
где — круг (проекция на плоскость ), а ,

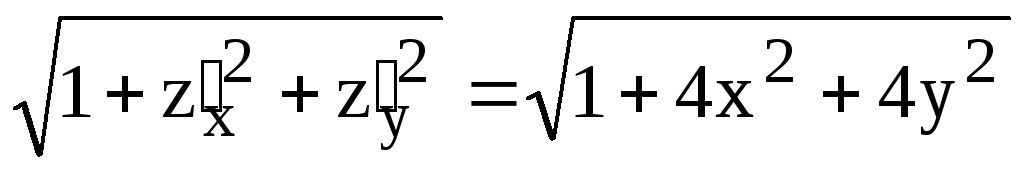окончательно имеем

.

ЗАНЯТИЕ 3: 4344, 4346, 4348.

ЗАДАНИЕ 3: 4343, 4345, 4349.

ЗАНЯТИЕ 3: 4362, 4365,

ЗАДАЧА. Найти поток векторного поля через полную поверхность конуса , изнутри этой поверхности.

ЗАДАНИЕ 4: 4364, 4366.

ЗАДАЧА. Найти поток векторного поля через внешнюю часть сферы , расположенную в первом октанте.