
МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО
ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
АЛТАЙСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Кафедра дифференциальных уравнений
Кафедра математического анализа
КРИВОЛИНЕЙНЫЕ И ПОВЕРХНОСТНЫЕ
ИНТЕГРАЛЫ И ИХ ПРИЛОЖЕНИЯ
Методические указания к практическим
занятиям по математическому анализу
для студентов физического факультета
Издание агу Барнаул 2000
КРИВОЛИНЕЙНЫЕ ПОВЕРХНОСТНЙЕ ИНТЕГРАЛЫ И ИХ ПРИЛОЖЕНИЯ: Методические указания к практическим занятиям по математическому анализу для студентов физического факультета. — Барнаул: изд. АГУ, 2000. 24с.
ПЕЧАТАЕТСЯ
По решению кафедр дифференциальных уравнений,
математического анализа и
методической комиссии МФ
Составители к.ф.-м.н., доцент ГончароваО.Н.,
доцент Саженкова Т. В.
Рецензент к.ф.-м.н., доцент Бушманов С. Б.
План УМД 2000г., п.42
Алтайский государственный университет, 2000
§1. Криволинейные интегралы
Формулы вычисления криволинейного интеграла первого рода по кривой L:
1)
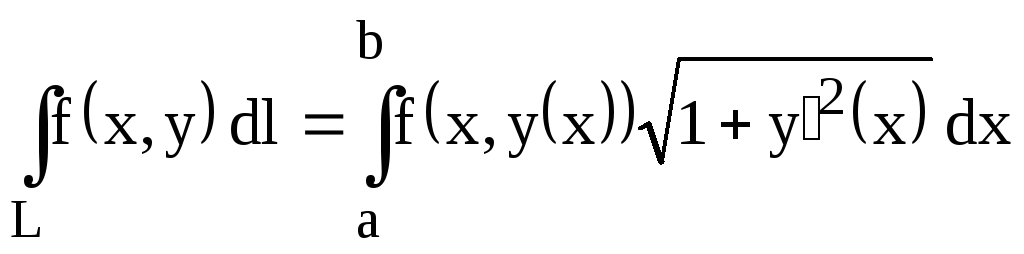
(кривая
L
задана в декартовых координатах:
![]() ),
),
2)

(кривая
L
задана параметрически:
![]() ),
),
3)
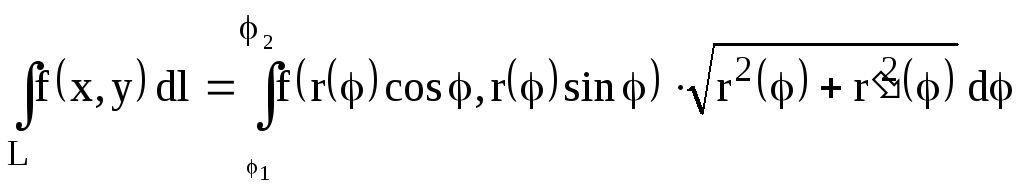
(кривая
L
задана в полярных координатах:
![]() ).
).
Формулы вычисления криволинейного интеграла второго рода вдоль кривой AB:
4)
![]()
(AB:
![]() ),
),
5)
![]()
(AB:
![]() ).
).
Циркуляцией Ц
векторного поля
![]() вдоль замкнутой кривой L
называется криволинейный интеграл
вдоль замкнутой кривой L
называется криволинейный интеграл
Ц=![]() .
.
Если
![]() ,
то
,
то
Ц=![]() .
.
Здесь
![]() — единичный касательный вектор к кривой
L
в точке M,
направленный в сторону обхода кривой.
Положительным направлением обхода
замкнутой кривой L
считается направление, при котором
область, ограниченная этой кривой,
остается слева (рис.1).
— единичный касательный вектор к кривой
L
в точке M,
направленный в сторону обхода кривой.
Положительным направлением обхода
замкнутой кривой L
считается направление, при котором
область, ограниченная этой кривой,
остается слева (рис.1).
ПРИМЕР 1. Вычислить
![]() ,
где C
— контур треугольника с вершинами
O(0,0),
A(1,0),
B(0,1).
,
где C
— контур треугольника с вершинами
O(0,0),
A(1,0),
B(0,1).
РЕШЕНИЕ: используя свойства криволинейного интеграла первого рода, можем написать:
![]() .
.
На
отрезке OB:
![]() ,
поэтому
,
поэтому
![]() .
.
На
отрезке OA:
![]() ,
следовательно,
,
следовательно,
![]() .
.
Отрезок
BA
лежит на прямой
![]() ,
поэтому
,
поэтому
![]() ,
,
![]() и
и
![]() .
.
Таким
образом,
![]() .
.
ПРИМЕР 2.
![]()
![]() .
.
![]()
![]() .
.
Положим
здесь
![]() ,
тогда
,
тогда
![]() .
.
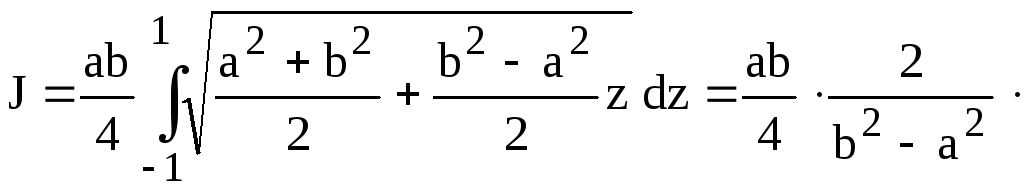
![]() .
.
ПРИМЕР3.
В ычислить
криволинейный интеграл
ычислить
криволинейный интеграл
![]() ,
,
где
![]() от точки
от точки
![]() до
до
![]() .
.
РЕШЕНИЕ:
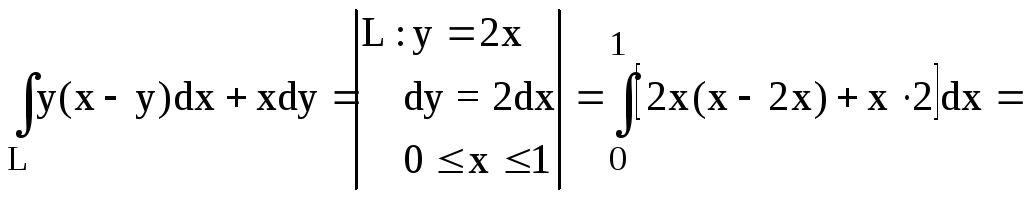
![]() .
.
ПРИМЕР 4.
Вычислить циркуляцию поля
![]()
вдоль
окружности
![]() (обход против хода часовой стрелки).
(обход против хода часовой стрелки).
РЕШЕНИЕ:
Ц=![]() ,
,
Ц=![]() ,
,
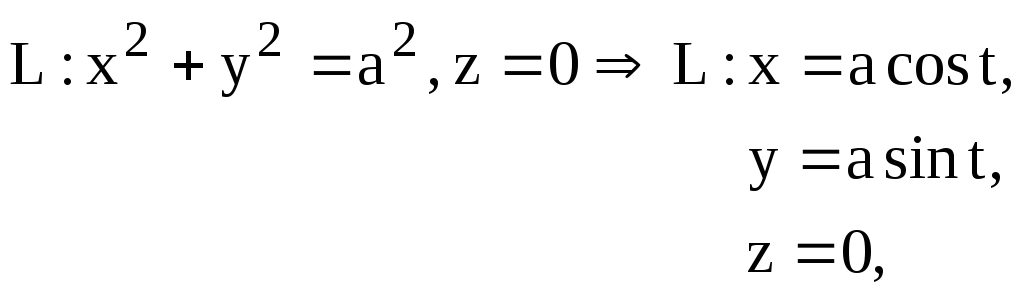
![]() ,
,
![]() ,
,
Ц=![]()
![]()
![]()
![]()
![]() .
.
Задачи, предлагаемые далее для аудиторной и самостоятельной работы, взяты из [3].
ЗАНЯТИЕ I: 4222, 4226, 4229, 4231.
ЗАДАНИЕ I: 4223, 4228, 4230, 4232.
ЗАНЯТИЕ 2: 4248, 4252, 4254, 4279.
ЗАДАНИЕ 2: 4249, 4251, 4255, 4230.
§2. Физические приложения криволинейных интегралов
1).
Пусть
![]() —материальная
плоская кривая с линейной плотностью
—материальная
плоская кривая с линейной плотностью
![]()
![]() —
масса кривой;
—
масса кривой;
2).
![]() ,
,
![]()
— статические
моменты кривой
![]() относительно осей
относительно осей
![]() и
и
![]() ;
;
3).
![]() —
координаты
центра тяжести кривой;
—
координаты
центра тяжести кривой;
4).
![]() —
момент
инерции кривой относительно начала
координат ( полярный момент инерции
кривой);
—
момент
инерции кривой относительно начала
координат ( полярный момент инерции
кривой);
5).
![]()
— моменты инерции
кривой относительно осей
![]() и
и
![]() ;
;
6).
![]() ,
,
![]() —
компоненты силы притяжения
—
компоненты силы притяжения
![]() материальной точки
материальной точки
![]() массы
массы
![]() материальной кривой
материальной кривой
![]() .
Здесь
.
Здесь
![]() ,
,
![]() —
угол между вектором
—
угол между вектором
![]() и осью
и осью
![]() ,
,
![]() —
гравитационная постоянная.
—
гравитационная постоянная.
Справедливы аналогичные формулы для вычисления массы координат центра тяжести и др., если
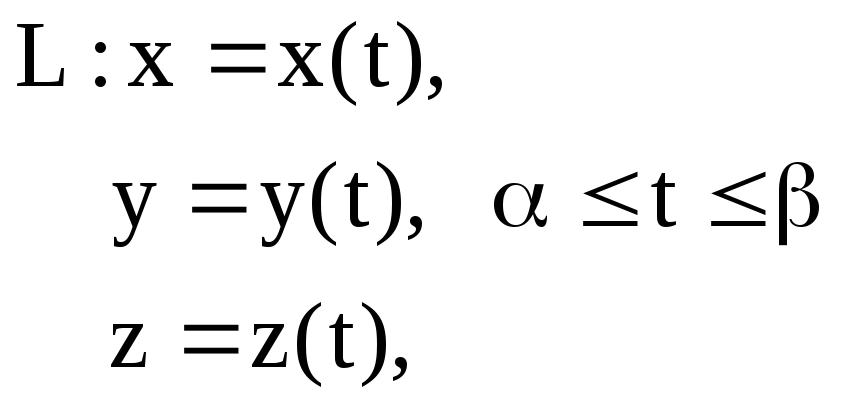 ,
,
![]() .
.
7).
![]() — работа
силы
— работа
силы
![]() при перемещение
материальной точки массы 1 из точки
при перемещение
материальной точки массы 1 из точки
![]() в точку
в точку
![]() вдоль кривой
вдоль кривой
![]() .
.
Аналогично вычисляется работа силы при перемещении материальной точки вдоль пространственной кривой.
8).
![]() — количество жидкости, вытекающей за
единицу времени из области
— количество жидкости, вытекающей за
единицу времени из области
![]() ,
ограниченной кривой
,
ограниченной кривой
![]() .
Здесь
.
Здесь
![]() —
скорость плоского потока жидкости в
точке
—
скорость плоского потока жидкости в
точке
![]() ;
;
![]() — единичный
вектор внешней нормали к кривой
— единичный
вектор внешней нормали к кривой
![]() в точке
в точке
![]() ;
;
![]() —
угол между
касательным вектором
—
угол между
касательным вектором
![]() к кривой
к кривой
![]() и осью
и осью
![]() .
Вектор
.
Вектор
![]() имеет
направление, соответствующее положительному
направлению обхода кривой.
имеет
направление, соответствующее положительному
направлению обхода кривой.
ПРИМЕР 5.
Найти
массу
![]() материальной кривой
материальной кривой
![]() ,
заданной уравнением
,
заданной уравнением
![]() ,
где
,
где
![]() ,
если линейная плотность ее в каждой
точке пропорциональна квадрату абсциссы.
,
если линейная плотность ее в каждой
точке пропорциональна квадрату абсциссы.
РЕШЕНИЕ: по формуле для массы (ІI.1) имеем
![]()
![]()
![]() .
.
ПРИМЕР 6.
Найти
координаты
![]() центра тяжести первого полсвитка
материальной винтовой линии
центра тяжести первого полсвитка
материальной винтовой линии
![]() ,
заданного уравнениями
,
заданного уравнениями
![]() ,
если ее линейная плотность постоянна
и равна
,
если ее линейная плотность постоянна
и равна
![]() .
.
