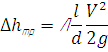22. Вывод уравнения движения вязкой жидкости Навье-Стокса

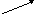
проекции силы силы

инерции массовые давления силы трения

силы

Ур-е, описывающее любое движение течения.

Эти диф. уравнения, описывают целый класс задач. Чтобы выделить конкретную задачу необходимо вводить условия однозначности:

1. физ. условия: ρ,μ = сonst

2. Геом. Условия (геометрия каналов)

3. Начальные условия. Задаются только для неустановившегося течения

4. Граничные условия. Задаются на границах потока. Самое распространенное ГУ- условие прилипания. Доказано, частица прилипая к пов-ти трубы на мгновение приобретает ск. движения трубы. Если труба неподвижна, то ск. на внутренней пов-ти трубы = 0

23. Решение уравнения Навье – Стокса при установившемся движении в плоской трубе.

1. Распределение скорости в плоской трубе.

Плоская труба – труба, состоящая из двух бесконечных плоскости по оси X и Z.

Нам необходимо найти распределение скорости

Физическая постановка:

1. Жидкость несжимаемая, вязкая

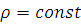
2. Движение установившиеся

3. Ламинарное

4. Так как течение ламинарное, проекции на ось X и Y будут отсутствовать

уравнение неразрывности

Из этого следует

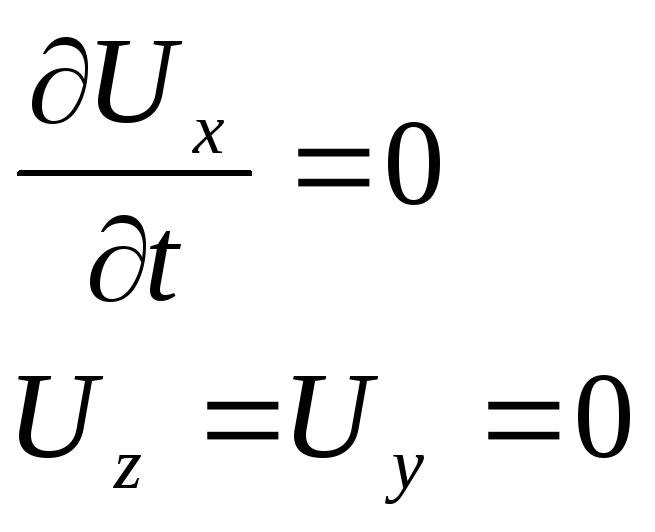Из этого следует

Жидкость находится только под действием силы тяжести

Но только Z нет стенки, значит нет силы трения

Функция зависит только от первой переменной

частный дифф-л -> полный дифф-л

ГУ: y=h, Ux=0 y=-h, Ux=0

перепад давления на произвольном участке

2C₁h=0

C₁=0

Уравнение Навье-Стокса

Уравнение неразрывности

24. Решение уравнения Навье – Стокса при установившемся движении в круглой трубе.

1. 

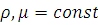
2. Движение установившиеся

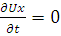
3. Течение ламинарное (Ur=U=0)

4. Движение сил симметричное

В следствии ламинарного потока будут отсутствовать проекции радиальной и круговой компоненты, то есть не будет ни (1) ни (2) уравнения.

Используя условия однозначности упрощаем уравнение Навье-Стокса

Жидкость находится только под действием силы тяжести

Переходим к полным дифференциалам

Интегрируем

из этого следует

ГУ:

При r = r_0, Ux=0

При r = 0,

Парабалический закон.

25. Опыты и графики Никурадзе и Мурина. Их основные отличия.

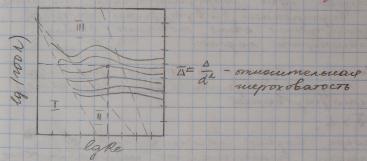
Цель опытов Никурадзе состоит в том, чтобы определить зависимость коэффициентов трения от числа Рейнольдса Re и относительной шероховатости.

Никурадзе искусственно создавал шероховатость, рассыпая по внутренней поверхности трубы частицы одинакового размера, такая шероховатость называется зернистой.

Никурадзе выделил 4 области сопротивления

1. Это область ламинарного течения

Re<2300

2. Область гидравлически гладких труб

Всегда при турбулентном течении на внутренней поверхности трубы формируется очень тонким связи ламинарным лоделой

Величина лоделоя больше размера , то тогла не образуется (вихоеватость) вихреобразования.

Когда вязкий ламинарный слой выше размера песчинок, то шероховатость не образует вихреобразной, такая труба называется гладкой

3. Область неустановившегося течения

4. Квадратичная (автомодельная) область

Опыты и графики Мурина

Цель опытов такая же

Подход другой;

Мурин исследовал естественную шероховатость технических труб. Исследовалась эквивалентная шероховатость.

Эквивалентная шероховатость – одна средняя шероховатость для технических труб, эффект от которой будет такой же при зернистой шероховатости.

Различия между опытами Никурадзе и Мурина

1. Никурадзе исследовал исскуственную зернистость. Мурин исследовал естественную зернистость поверхности.

2. Мурин не исследовал область ламинарного движения

3. Никурадзе – в lg

Мурин – в опытах корд