17.Энергетический и геометрический смысл слагаемых уравнения Бернулли.

Энергетический смысл.

В таком виде уравнение Бернулли представляет собой закон сохранения энергии, отнесенный к единице массы.

1) - удельная кинетическая энергия

2) - удельная потенциальная энергия давления

3) - удельная потенциальная энергия положения

1),2),3) – удельная полная механическая энергия

2),3) – удельная потенциальная энергия

Геометрический смысл.

пьезометры

трубки Пито

линия полного напора

поверхность сравнения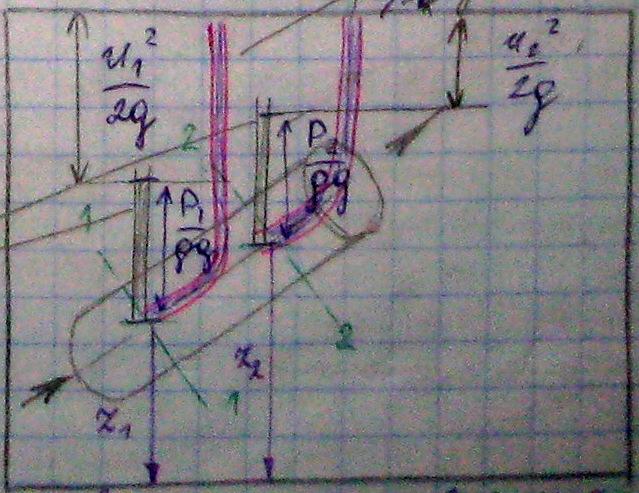

z₁,z₂ – нивелирные высоты – расстояние от центров до поверхности сравнения

- пьезометрические высоты

- пьезометрические напоры

- динамические (скоростные) напоры

18.Вывод уравнения Бернулли для элементарной струйки вязкой жидкости.

Для того, чтобы полученное ранее уравнение для идеальной струйки жидкости применить к реальной жидкости

- в единицах напора

- потеря напора

При движении реальной жидкости между ее слоями возникает сила трения, т.е. часть механической энергии переходит в теплоту. Если скорость жидкости небольшая, то ее температура не повышается.

Закон сохранения энергии

- в единицах энергии

e_W – потерянная энергия

ΔP_W – потерянное давление(напор/удельная энергия)

Гидравлические сопротивления

Δh_дл - Потерянная энергия, отнесенная к весу жидкости, называется потерями напора по длине

Δh_м – местные потери( возникает внезапно, когда меняется размер сечения или направление движения)

19. Вывод уравнения Бернулли для всего потока. Условие применяемости.

Уравнение для всего потока.

Это уравнение можно получить пуьем суммирования энергий всех струек. Для этого умножим полученное только что уравнение на массовый расход (ρudF) и проинтегрируем его по сечению.

Проинтегрировать это уравнение можно только в том случае, если ввести понятие о плавно или медленно изменяющемся потоке. Для этого потока доказано, что:

радиус кривизны → ∞

Введем коэффициент Королиса α

Подставим полученные выражения в уравнение, предварительно разделив на ρQ

α– коэффициент Кориолиса – поправочный коэффициент на скорость (кинетической энергии), который зависит от режима течения жидкости)

α_лам=2

α_турб=1,1

Условия применимости уравнения Бернулли

1. ρ=const

2. установившееся движение

3. поток изменяется плавно или медленно

20.Режимы течения жидкости. Опыт Рейнольдса

Опыты проводились при постоянном напоре Н и опр-ся расход Q. (Q=V*F, м³/с) Опыт проводился с увеличением скорости V и было обнаружено, что до определенного значения критической скорости течение имело слоистый характер. Это ламинарное течение, а хаотичное- турбулентное. Когда Рейнольдс провел опыт в обратном направлении, оказалось что переход из турбулентного режима в ламинарный произошел при другом течении скорости. Поэтому Рейнольдс сделал вывод, что существует переходная область между ламинарным и турбулентным режимом. В этой области режим течения может быть и ламинарным и турбулентным. Рейнольдс, определил факторы, влияющие на режим течения: скорость, вязкость, плотность, гидравл. диаметр.

Критерий Р. - физ. смысл Р.

Если Re меньше 2300- ламинарное течение, если больше – турбулентное

По опытам, верхним числом Р. является 1,3 * 10⁴= Re_кр.

d₂=4F\ =4пл. живого сечения\ смоченный диаметр

Живое сечение- поперечное сечение потока жидкости

Смоченный диаметр- периметр, где жидкость соприкасается с внутренними стенками.