
- •Введение
- •1.2 Составление функционально -структурной схемы выбранной системы
- •1.3 Определение передаточных функций элементов функционально –структурной схеме
- •1.4 Составление и преобразование структурной схемы и расчет передаточной функции для замкнутой и разомкнутой систем
- •1.5 Определение устойчивости системы
- •1.7 Определение показателей качества системы
- •2.1 Преобразование нелинейной системы
- •Построение фазового портрета и переходного процесса
- •Список литературы
1.7 Определение показателей качества системы
Для определения прямых оценок качества системы воспользуемся переходным процессом (рисунок 6)
-
Время регулирования – это время регулирования, за которое переходной процесс выходит в 5%-трубку.
tр=27 с
-
Время первого согласования – это время, за которое система в первый раз достигает установившегося состояния.
tс=7 с
-
Время нарастания – это время, при котором выходная величина достигает максимального значения.
tн=10 с
-
Перерегулирование, которое определяет отклонение регулируемой величины от установившегося значения (динамическая ошибка системы).
![]() (монотонный процесс)
(монотонный процесс)
-
Колебательность – это число колебаний системы от момента воздействия на нее до перехода в установившееся состояние.
n=1
Для определения косвенных оценок качества системы воспользуемся АЧХ системы (рисунок 7).
-
Частота среза – это частота, при которой амплитуда равна единице.
![]() 0,1
с-1
0,1
с-1
-
Резонансная частота – это частота, при которой амплитуда имеет максимальное значение.
![]() 0
с-1
0
с-1
-
Максимальное значение амплитуды:
![]()
-
Амплитуда при нулевой частоте:
А(0)=1,2
-
Показатель колебательности:
![]()
-
Полоса пропускания:
![]()
-
Время регулирования:
![]()
![]() с
с
![]()
![]() с
с
125,6 c<tp<0 c
1.8 Построение логарифмических частотных характеристик системы, оценка запасов устойчивости
С помощью логарифмических частотных характеристик исследуется устойчивость замкнутой системы. Построение ЛАЧХ и ЛФЧХ ведется для разомкнутой системы, которая имеет передаточную функцию:
![]()
ЛАЧХ и ЛФЧХ систем изображены на рисунке 8.

Рисунок 8 - ЛАЧХ и ЛФЧХ системы
Запас устойчивости по амплитуде составляет 39,3 дБ.
Запас устойчивости по фазе бесконечен.
Вывод: Анализ линейной части системы регулирования давления пара перед турбиной энергоблока показывает, что при заданных параметрах система устойчива с большим запасом устойчивости по амплитуде. Запас устойчивости по фазе бесконечен.
2. ИССЛЕДОВАНИЕ НЕЛИНЕЙНОЙ СИСТЕМЫ
2.1 Преобразование нелинейной системы
Заменим второе звено (электро - механическая задвижка) линейной части системы регулирования давления пара на нелинейный элемент. На рисунке 9 изображена структурная схема с нелинейным элементом
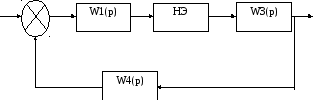
Рисунок 9 - Структурная схема с нелинейной системы регулирования
 Для
построения фазового портрета структурную
схему преобразуем так, чтобы нелинейный
элемент и линейная часть были соединены
последовательно.
Для
построения фазового портрета структурную
схему преобразуем так, чтобы нелинейный
элемент и линейная часть были соединены
последовательно.
х(t)
g
НЭ ЛЧ![]() (t)
g(t) y(t)
(t)
g(t) y(t)








Рисунок 10 - Преобразованная структурная схема нелинейной системы
Передаточная функция линейной части:
![]()
![]()
Метод фазовых портретов предназначен для анализа нелинейных систем не выше второго порядка. Преобразуем передаточную функцию линейной части.
![]()
