1.5 Определение устойчивости системы

Определим устойчивость системы по критерию Гурвица. Выпишем характеристическое уравнение системы:

Для устойчивости системы необходимо и достаточно, чтобы все миноры определителя Гурвица были положительны. Определитель Гурвица составим по коэффициентам характеристического уравнения.

Все миноры определителя Гурвица положительны, следовательно, система устойчива.

Определим устойчивость системы по критерию Найквиста. Расчет по критерию Найквиста производится для разомкнутой системы.

Для устойчивости системы в замкнутом состоянии необходимо и достаточно, чтобы корни полинома разомкнутой системы находились в левой части комплексной плоскости и годограф Найквиста не охватывал точку (-1;j0).

Передаточная функция замкнутой системы регулирования давления пара имеет вид:

Возьмем полином разомкнутой системы и определим количество корней:

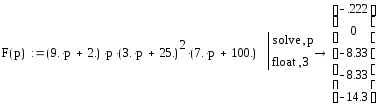
Все корни полинома разомкнутой системы находятся в левой части комплексной плоскости.

Построим годограф Найквиста (рисунок 5) с помощью программы MathLab:

>> w=tf([57062.5],[567 17676 178275 601250 125000])

Transfer function:

5.706e004

----------------------------------------------------

567 s^4 + 17676 s^3 + 178275 s^2 + 601250 s + 125000

>> pole(w)

ans =

-14.2857

-8.3333 + 0.0000i

-8.3333 - 0.0000i

-0.2222

>> zero(w)

ans =

Empty matrix: 0-by-1

>> nyquist(w)

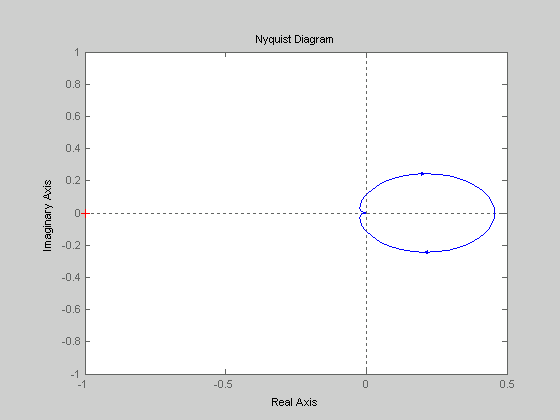
Рисунок 5 - Годограф Найквиста разомкнутой системы

Годограф Найквиста не охватывает точку (-1;j0).

Значит, система регулирования давления пара в замкнутом состоянии будет устойчива, т. к. корни полинома разомкнутой системы находятся в левой части комплексной плоскости и годограф Найквиста не охватывал точку (-1;j0).

1.6 Построение переходной функции и амплитудно – частотной

характеристики

Для определения различных показателей качества необходимо построить переходную функцию и амплитудно – частотную характеристику.

Переходным процессом называют изменение во времени состояния параметров системы с момента появления управляющего или возмущающего момента на систему находившуюся в установившемся состоянии.

Переходная функция системы h(t) – это функция определяющая изменение выходной величины системы, при подаче на вход единичного ступенчатого воздействия.

Переходная функция системы регулирования давления пара будет иметь вид:

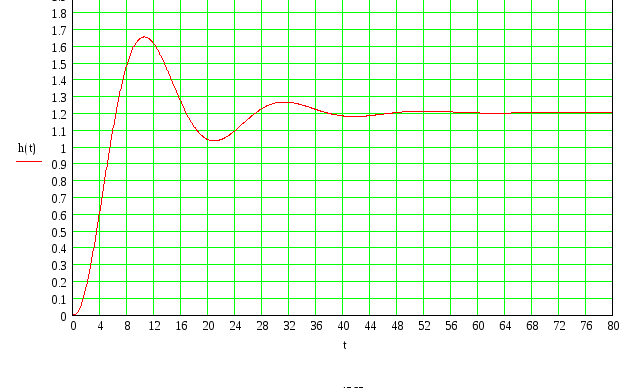
Рисунок 6 - Переходной процесс системы регулирования давления пара

Для построения амплитудно – частотной характеристики (АЧХ) необходимо заменить в передаточной функции замкнутой системы оператор р на j*.

АЧХ будет иметь вид:

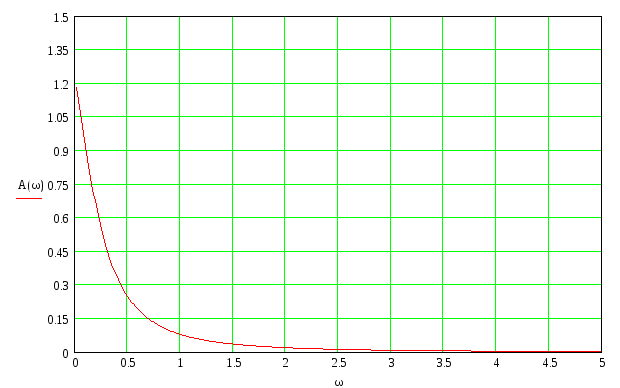
Рисунок 7 - АЧХ системы регулирования давления пара