§4. Формула Остроградского-Гаусса

Формула Остроградского-Гаусса является аналогом формулы Грина-Остроградского для случая пространственной области.

Теорема. Пусть (S) - замкнутая кусочно-гладкая поверхность, ограничивающая тело (V) в пространстве. Пусть выбрана внешняя сторона поверхности. Пусть P, Q, R - функции, имеющие непрерывные частные производные на (V). Тогда имеет место формула ОстроградскогоГаусса:

(1)

или

, (2)

где , ,  - углы нормали к внешней стороне поверхности (S) с координатными осями OX, OY, OZ.

Доказательство.

Будем считать, что поверхность (S) можно разбить на три части: (S₁),

заданную уравнением z=f₁(x;y), (S₂), заданную уравнением z=f₂(x;y) и (S₃) - цилиндрическую поверхность с образующей, параллельной оси OZ. Функции f₁(x;y), f₂(x;y) непрерывны в замкнутой области (D), которая является проекцией (S) на плоскость XOY.

Вычислим интеграл:

.

Выберем внешнюю сторону поверхности, и полученные двойные интегралы заменим поверхностными интегралами второго рода. На (S₁) направляющий косинус cos<0, на (S₂) cos>0, а на (S₃) cos=0. Тогда по теореме §3

,.

Прибавим , получим

.

Следовательно, .

Если поверхность S можно представить в виде объединения поверхностей x=x₁(y;z), x=x₂(y;z), (y;z)(D_yz) и цилиндрической поверхности, с образующей параллельной оси OX, то , и, при аналогичных условиях . Тогда, складывая I₁+I₂+I₃ получим формулу (1).

Теперь предположим, что (V) состоит из конечного числа тел, разделенных гладкими поверхностями , причем эти тела удовлетворяют сформулированным выше условиям. Для удобства, пусть . Тогда

Каждый из интегралов преобразуем по формуле Остроградского-Гаусса как , где взяты внешние стороны поверхностей (S_i), i=1,2. Поверхности (S₁), (S₂) имеют общую часть , причем их внешние нормали противоположны. Следовательно, интегралы по части взаимно сократятся, поэтому:

.

Таким образом, и в этом случае получаем формулу Остроградского-Гаусса.

Аналогичные рассуждения можно провести для большего числа частей тела (V).

Замечание. Формула Остроградского-Гаусса позволяет легко получить формулу для вычисления объема V тела (V) с помощью поверхностного интеграла по поверхности, ограничивающей тело (V). Действительно, если в формуле (1) положить P(x;y;z)=x, Q(x;y;z)=y, R(x;y;z)=z, то получим

или .

Пример. Вычислить интеграл, используя формулу Остроградского-Гаусса:

, где (S) – внешняя сторона пирамиды, составленной плоскостями x=0, y=0, z=0, x+y+z=1.

 P(x;y;z)=xz, Q(x;y;z)=xy, R(x;y;z)=yz,

Применим формулу Остроградского-Гаусса:

. 

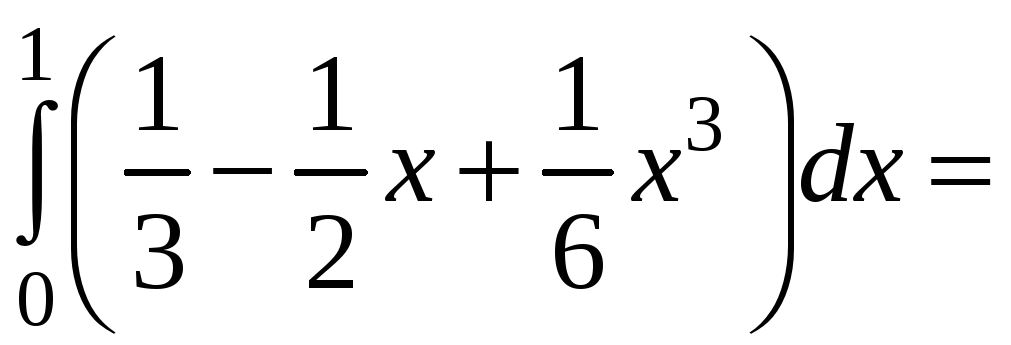
§5. Формула Стокса

Теорема. Пусть (S) - гладкая ориентированная двусторонняя поверхность (т.е. направление нормали выбрано, образует с положительным направлением оси OZ острый угол) и l - кусочно-гладкая кривая, ограничивающая (S), причем мы считаем направление обхода l положительным. Пусть функции P, Q, R - непрерывно дифференцируемые. Тогда

или

,

где cos, cos, cos - направляющие косинусы нормали поверхности.

Доказательство.

Пусть уравнение поверхности имеет вид z=f(x;y).

Вычислим, например, . Пусть проекция L кривой l на плоскость XOY задана параметрическими уравнениями: (x(t), y(t) - непрерывно дифференцируемые функции). Тогда

.

К плоской кривой L применим формулу Грина:

,

где (D) - ограничиваемая кривой L область плоскости XOY.

Так как 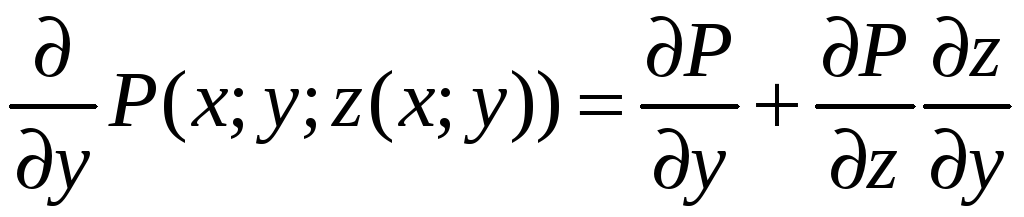, то

.

Пусть , ,  - углы нормали к внешней стороне поверхности (S) с координатными осями OX, OY, OZ. Направляющие косинусы вычисляются по формулам (4) (см. §3).

Так как dxdy=cosdS, 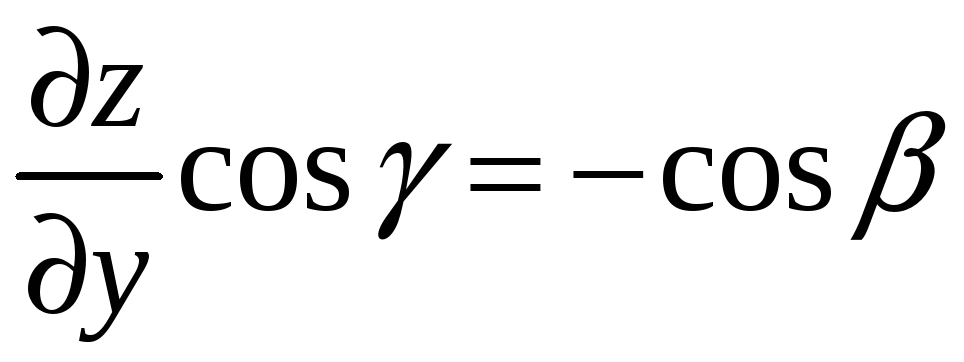, то .

Поэтому .

Следовательно, .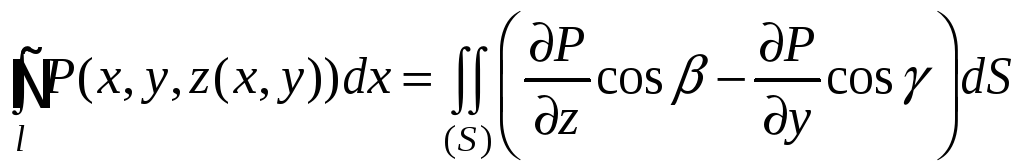

Аналогично, устанавливаются соотношения:

и .

Складываем:

.

Формула Стокса доказана.

Замечание 1. В случае плоской кривой L (поверхность (S) представляет собой плоскую область (D)), лежащей на плоскости XOY (z=0), эта формула совпадает с формулой Грина:

.

Замечание 2. Формулы в правой части запомнить непросто. Поэтому удобно записать подынтегральное выражение в виде своеобразного определителя .

Во второй строке стоят операторы дифференцирования. Поэтому будем считать, что мы понимаем под этим определителем его формальное разложение по первой строке, причем произведение, например, оператора на функцию R есть и т.п.