2. Вычисление поверхностного интеграла 2 рода

Теорема. Пусть двусторонняя поверхность (S) задана явным уравнением z=z(x;y), причем z(x;y) и ее частные производные и существуют и непрерывны в простой области (D_xy), которая является проекцией поверхности (S) на плоскость XOY. Пусть в каждой точке поверхности (S) задана непрерывная функция f(x;y;z). Тогда поверхностный интеграл по верхней и нижней стороне поверхности (S) существует и выражается через двойной интеграл для верхней стороны поверхности (S):

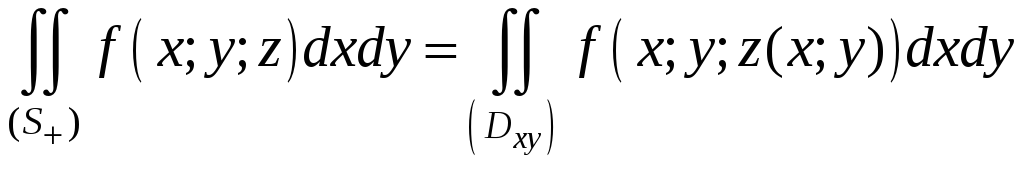(1)

и соответственно для нижней стороны поверхности (S):

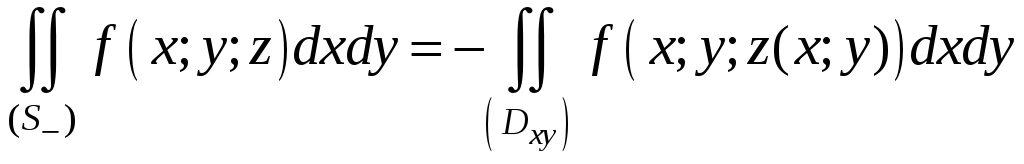. (2)

Доказательство.

В силу условий теоремы интегралы в равенствах (1) и (2) существуют. Докажем эти равенства. Составим интегральную сумму для поверхностного интеграла второго рода по верхней стороне поверхности: 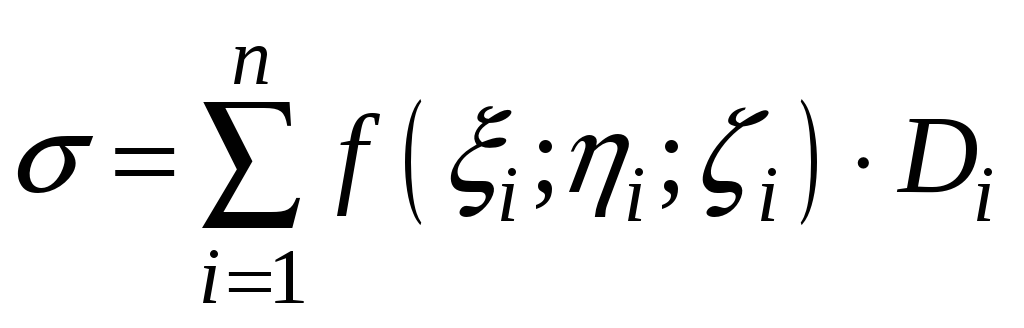. Т к. точка принадлежит поверхности, то . Тогда

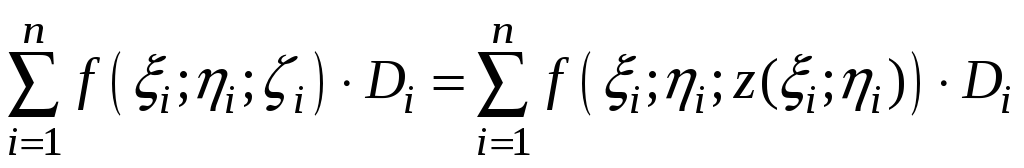. (3)

В правой части стоит интегральная сумма для двойного интеграла 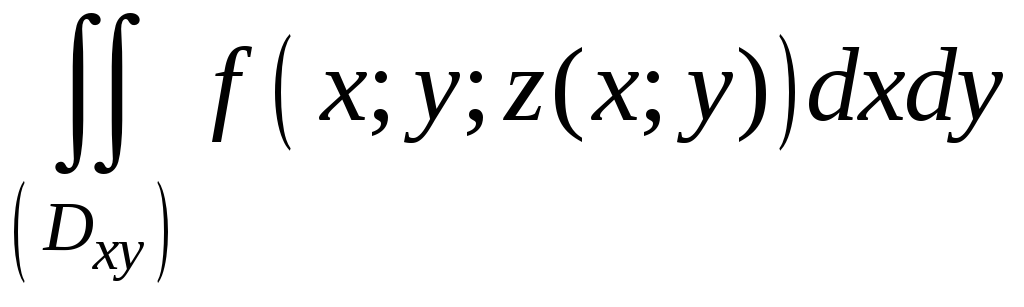. Переходя к пределу при 0, получим равенство (1).

Если поверхностный интеграл берется по нижней стороне поверхности, то в интегральной сумме все D_i отрицательны, и получим формулу (2).

Таким образом, вычисление поверхностного интеграла второго рода сводится к вычислению обычного двойного интеграла по области (D) от функции f, в которую вместо координаты z подставлено ее выражение из уравнения поверхности (S).

Обобщая эти рассуждения, получим:

=

,

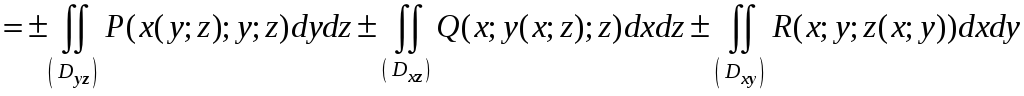г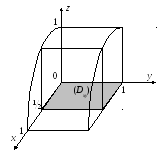де (D_xy), (D_xz), (D_yz) – это соответствующие проекции поверхности (S) на плоскости XOY, XOZ, YOZ.

Пример. Вычислить поверхностный интеграл второго рода: 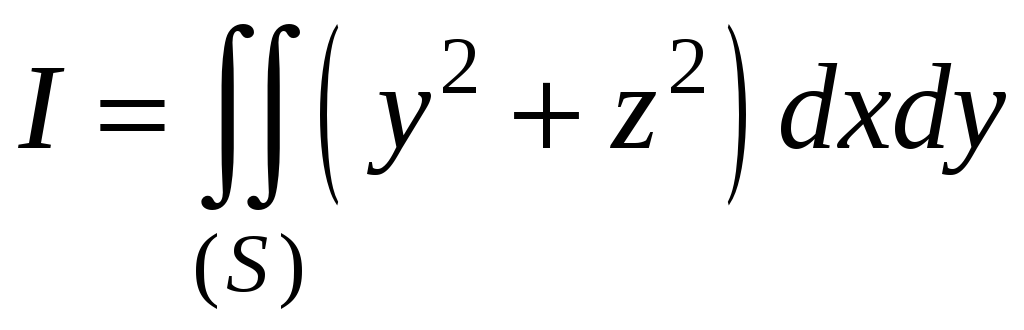, где (S) - это верхняя сторона поверхности , отсеченная плоскостями y=0, y=1, x=0 и .

 Уравнение задает цилиндрическую поверхность, образующими которой являются прямые, параллельные оси ординат, а направляющей является часть окружности.

Область (D_xy) имеет вид: 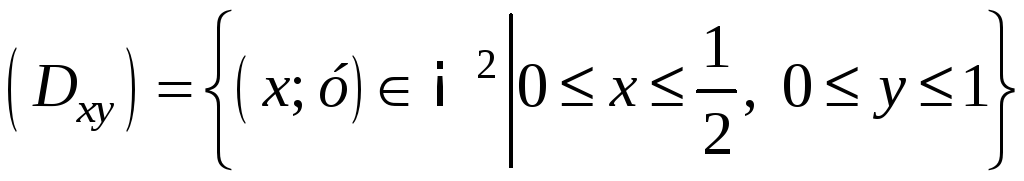, функция , следовательно, .



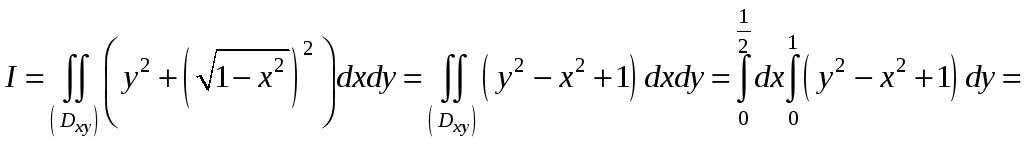
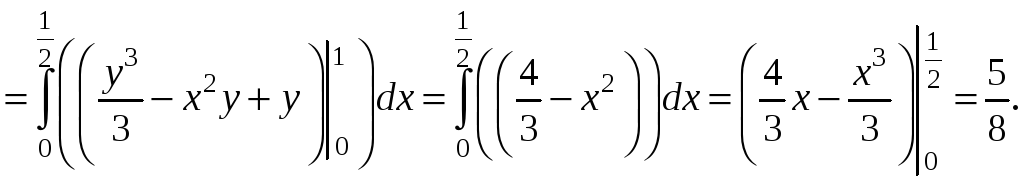
3. Связь между поверхностными интегралами второго рода и первого рода

Р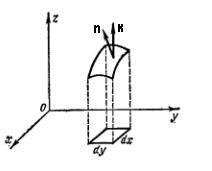ассмотрим поверхностные интегралы первого и второго рода по двусторонней поверхности (S), нормаль к которой образует углы ,  и  соответственно с координатными осями ОX, OY и OZ .

Будем считать, что двусторонняя поверхность (S) задана явным уравнением z=z(x;y), причем z(x;y) и ее частные производные и существуют и непрерывны в простой области (D) плоскости XOY. Нормаль к поверхности (S) , как вектор, ортогональный к касательной плоскости, имеет координаты: , и направляющие косинусы нормали равны:

,

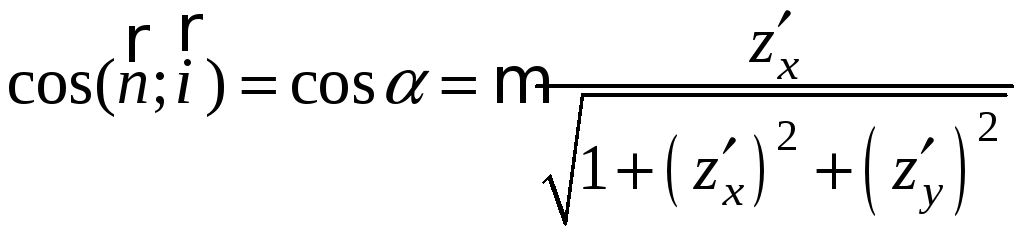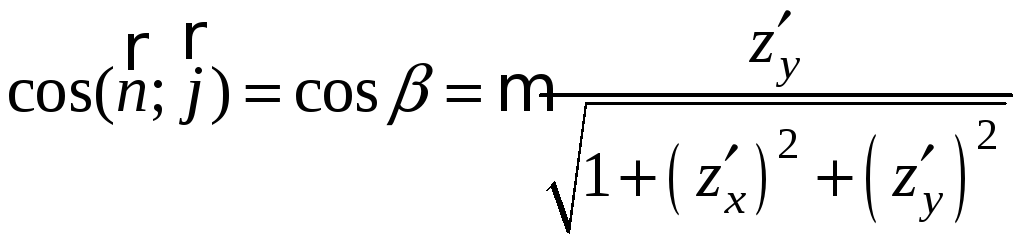, (4)

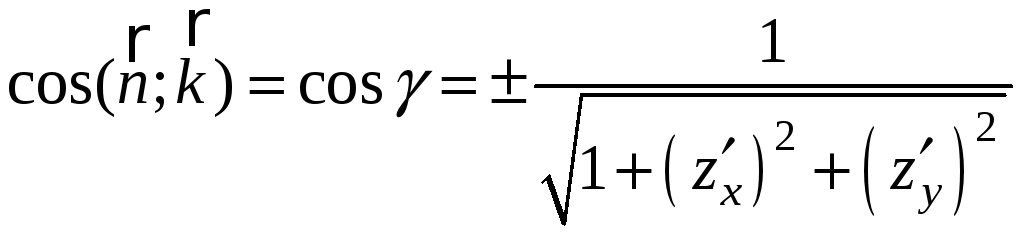
Выбор знака перед радикалом соответствует острому или тупому углу нормали с соответствующей осью координат и определяет сторону поверхности (S).

Покажем, что . (5)

Пусть вначале выбрана верхняя сторона поверхности, и угол  острый. Тогда по теореме о вычислении поверхностного интеграла второго рода

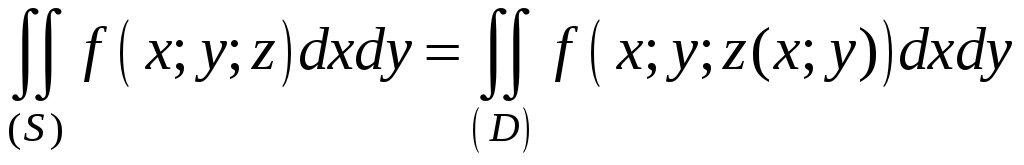. (6)

С другой стороны,

.

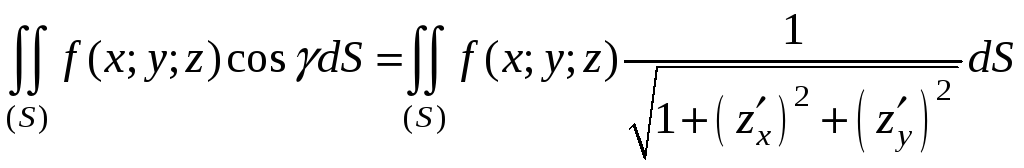Учитывая, что дифференциал площади , по теореме о вычислении поверхностного интеграла 1 рода получим

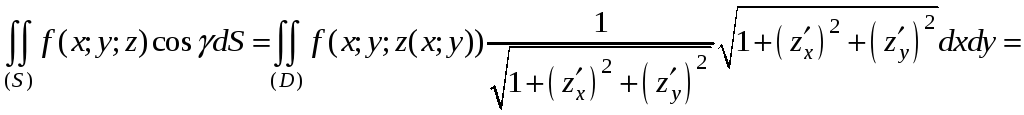
. (7)

Из равенства правых частей равенств (6) и (7) следует равенство левых, то есть получаем (5).

Заменяя верхнюю сторону поверхности нижней, мы тем самым меняем знак левой части равенства (5). Так как нормаль в этом случае направлена вниз, то угол  будет тупым, значит, cos<0, и правая часть тоже поменяет знак. Следовательно, равенство сохранится.

Аналогично можно доказать и более общее соотношение

,

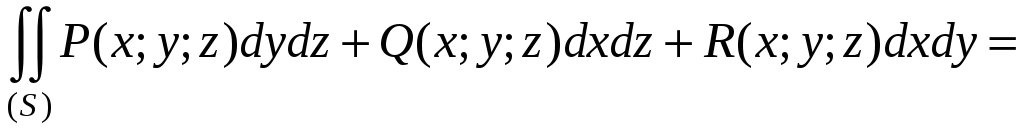
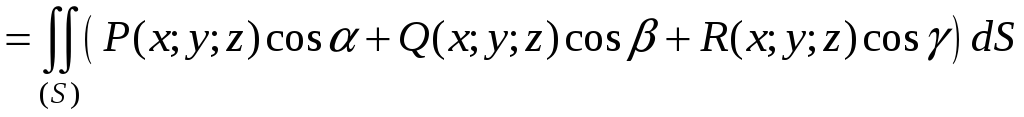где P, Q, R – функции от (x;y;z), определенные в точках поверхности (S), и интегралы в правой и левой частях равенства существуют.

Подчеркнем, что справа стоят направляющие косинусы нормали, соответствующей той стороне поверхности, по которой берется интеграл слева.