3. Основные свойства криволинейного интеграла II типа

1º. Если функция f интегрируема вдоль кривой AB, , то функция kf также интегрируема вдоль кривой AB, причем

.

2º. Если функции f и g интегрируемы вдоль кривой AB, то и функция fg интегрируема вдоль кривой AB, причем

.

3º. (Аддитивность)

Для любой точки C кривой AB, если интегрируема вдоль кривой AB, то она интегрируема и вдоль кривых AС и СВ и

.

4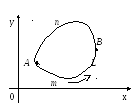º. Если функция интегрируема вдоль кривой AB, то она интегрируема и вдоль кривой ВА, причем

.

5º. Если интегрируема по замкнутому контуру L, то величина криволинейного интеграла не зависит от того, какую точку контура принять за начальную:.

Действительно, из рисунка видно

.

6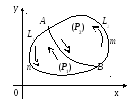º. Если область (P), ограниченную замкнутым контуром L разделить на две области (P₁) и (P₂), ограниченные контурами L₁ и L₂ соответственно, то интеграл в некотором направлении по кривой L равен сумме интегралов по контурам L₁ и L₂ в том же направлении:

.

Доказательство.

.

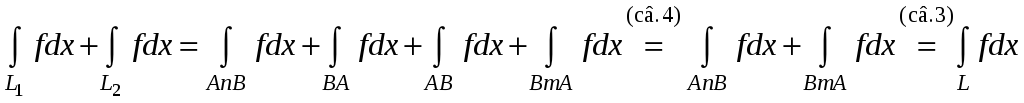4.Существование и вычисление криволинейных интегралов II типа

Теорема. Пусть кривая L=AB задана параметрическими уравнениями

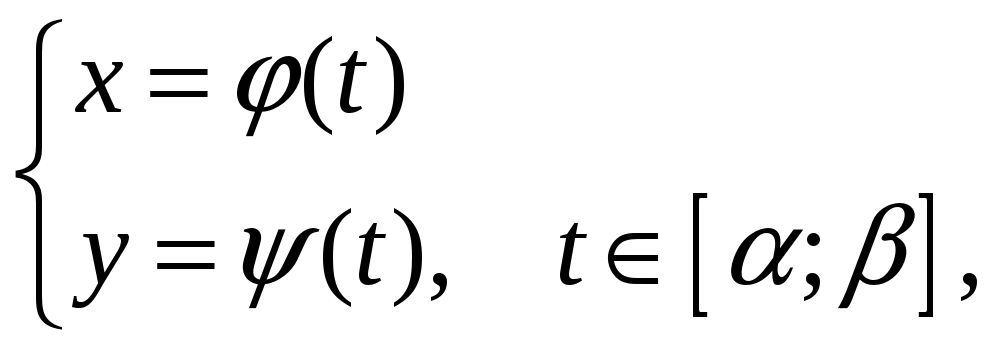
где и - непрерывно дифференцируемые функции на [;]. При изменении параметра t от  до  кривая описывается от точки A к точке B. Пусть функции f(x;y), P(x;y), Q(x;y) непрерывны на кривой L (т. е. M₀L 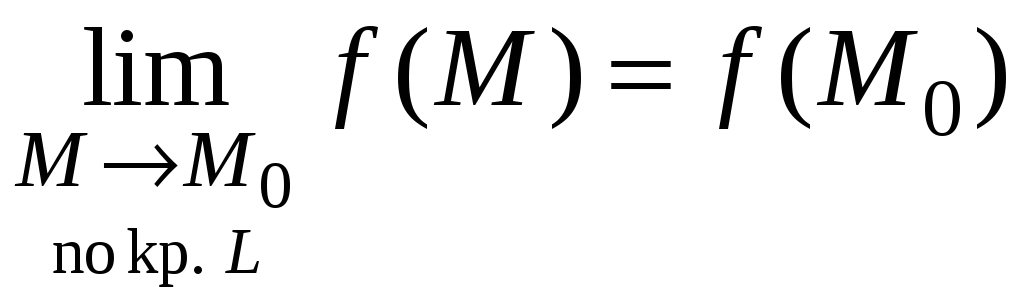). Тогда существуют , , и справедливы соотношения:

1) ,

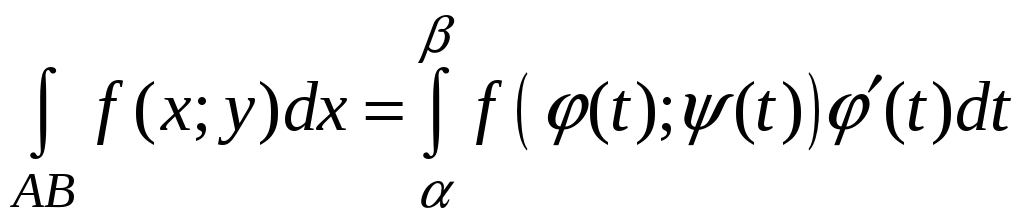2) ,

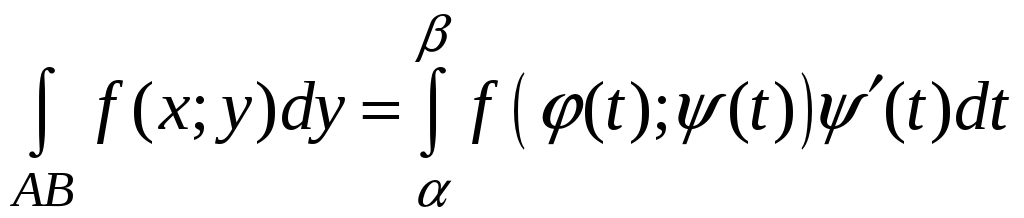3) .

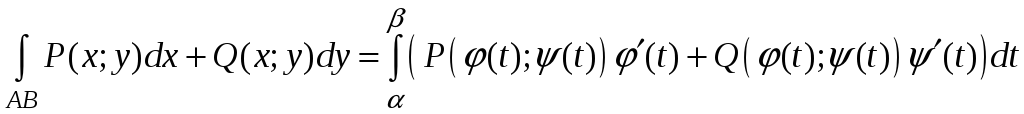Доказательство.

Докажем существование и равенство 1).

Возьмем произвольное разбиение кривой точками на n частичных дуг. Выберем произвольные точки и составим интегральную сумму

,

, .

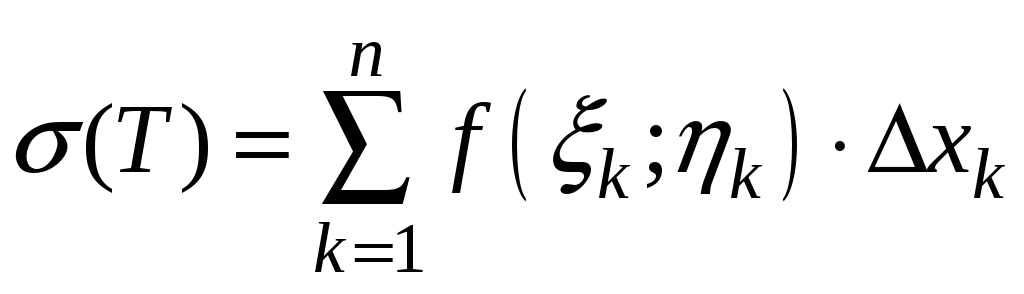
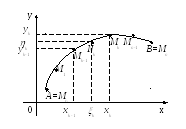Обозначим через t_k значение параметра t, которому соответствует точка , а через _k - значение t, которому соответствует точка . Тогда

.

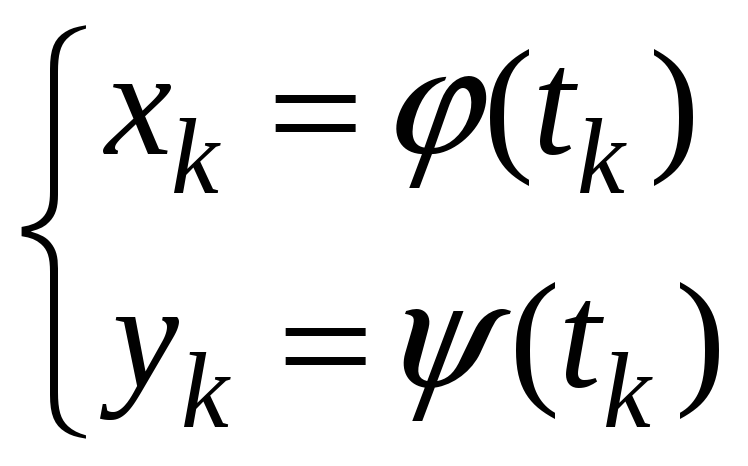
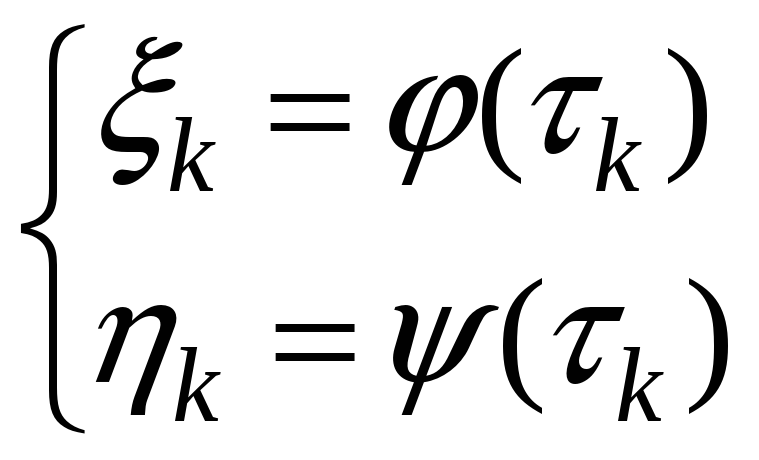Подставим эти соотношения в :

.

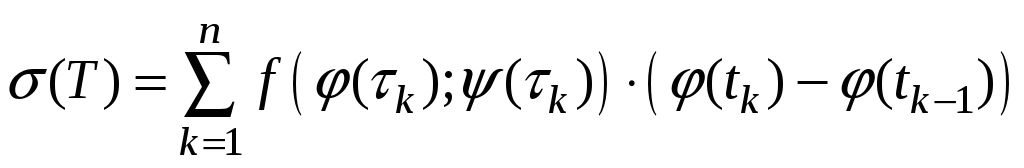Согласно формуле Ньютона-Лейбница 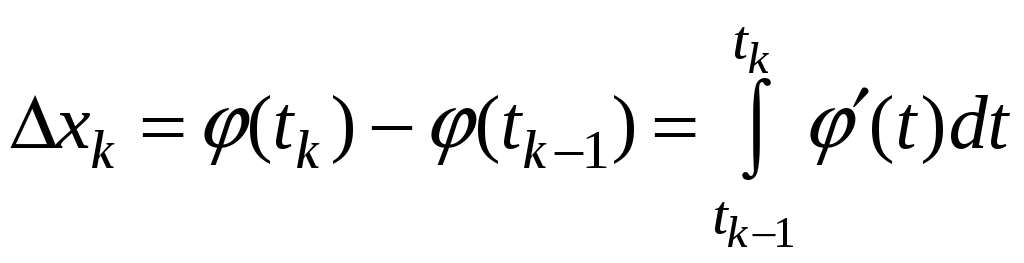. Подставляя в последнее равенство, получим:

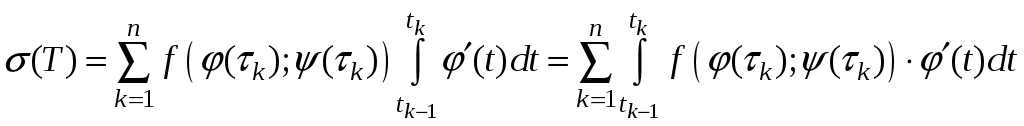. (5)

По условию f(x;y) непрерывна вдоль L, (t), (t), (t) непрерывны на [;], следовательно, функция f((t);(t))(t) интегрируема на [;].

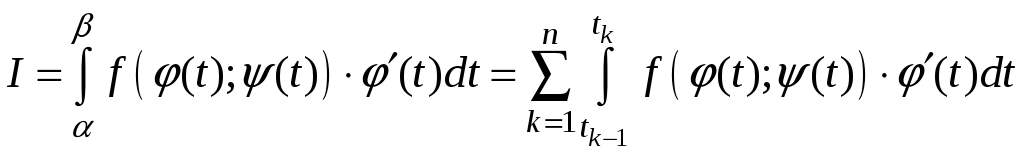. (6)

Рассмотрим разность . Из (5), (6) следует

.

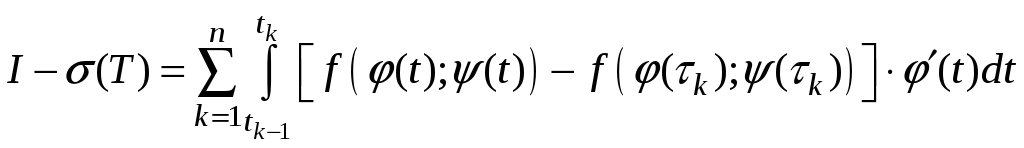Оценим модуль этой разности:

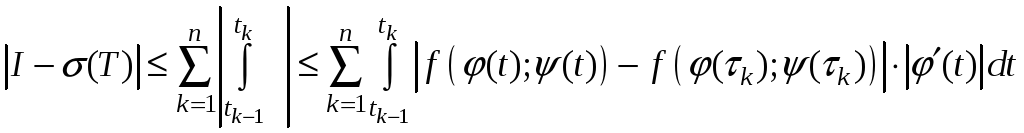. (7)

Так как непрерывна на [;], то она ограничена на [;], то есть выполнено . (8)

Так как непрерывна на [;], то она равномерно непрерывна на [;], то есть выполнено

. (9)

Если разбиение Т взять таким образом, что , то есть , то . Следовательно, для таких t выполнено (9):

. (10)

Тогда из (7), учитывая (8), (10), получим

.

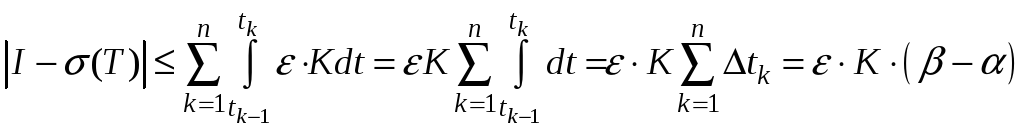Таким образом, выполнено

. (11)

Обозначим . Тогда из (11) следует, что

. (12)

Если , то и 0. Тогда

.

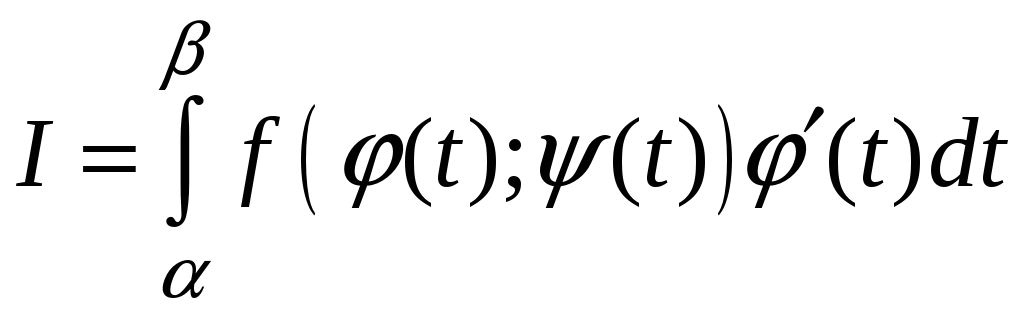 , и т.к. , , то

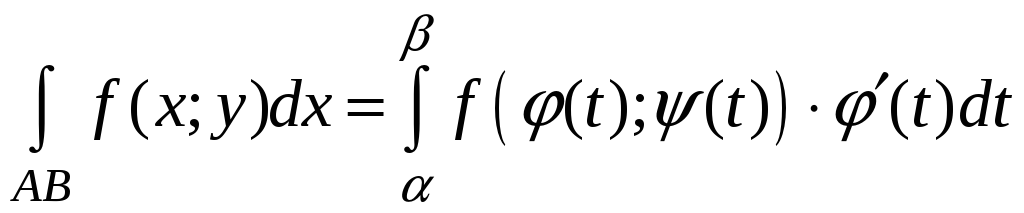, то есть верно равенство 1).

Замечание 1. Пусть кривая АВ задана явным уравнением y=(x), где  определена и непрерывна вместе с на [a;b], A=(a), B=(b). Пусть f непрерывна на кривой АВ. Тогда

, .

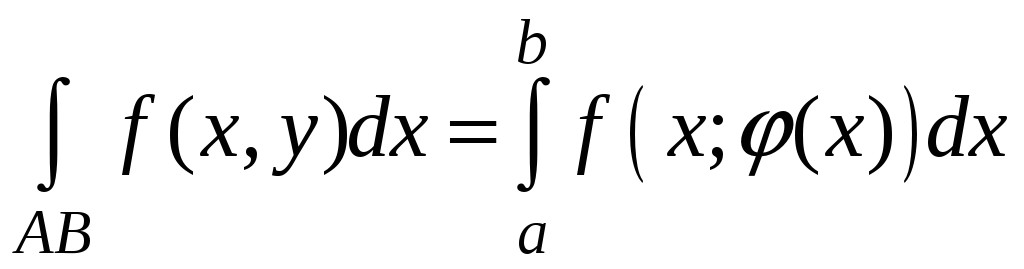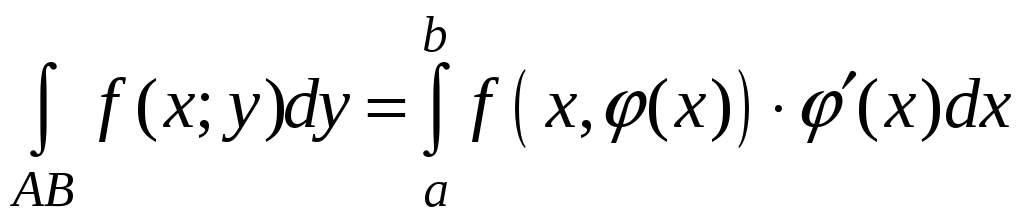Аналогично, если кривая АB задана уравнением x=(y), y[c;d], где (y) непрерывно-дифференцируема на [c;d], то

, .

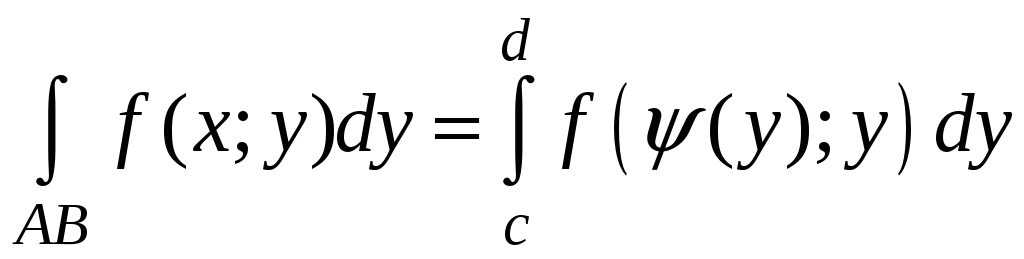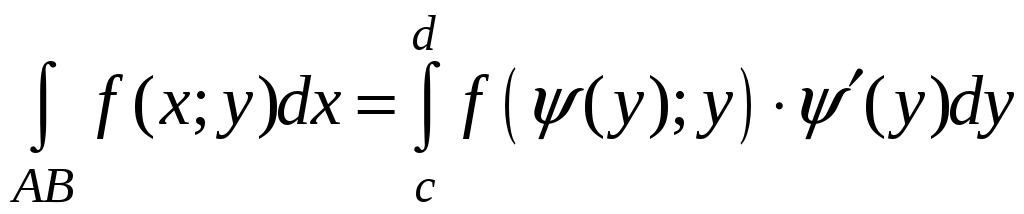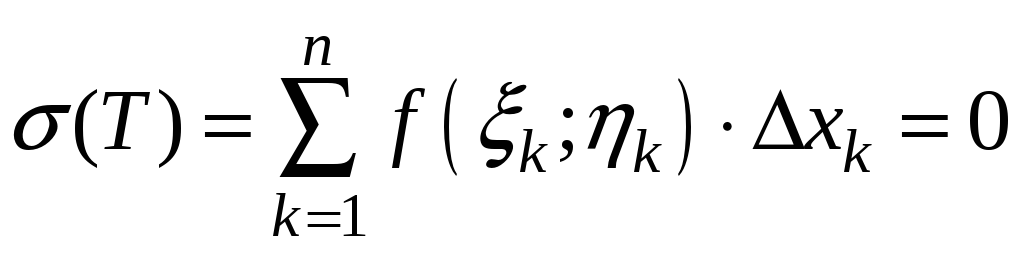Замечание 2. Если кривая АВ представляет собой отрезок, параллельный оси Oy, то . Это следует из того, что в интегральной сумме =0 , следовательно, . Отсюда . Аналогично, если АВ – отрезок, параллельный оси Ox, то .

Пример 1. Вычислить , если L - дуга параболы y=x² от точки (0;0) до точки (2;4).

Δ I способ. y=x²  dy=2xdx, x[0;2].

.

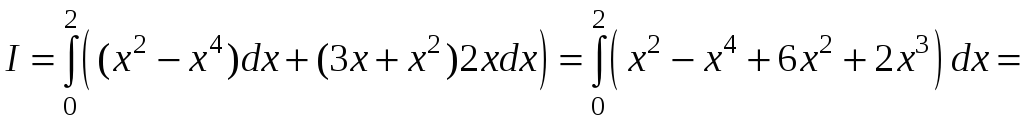
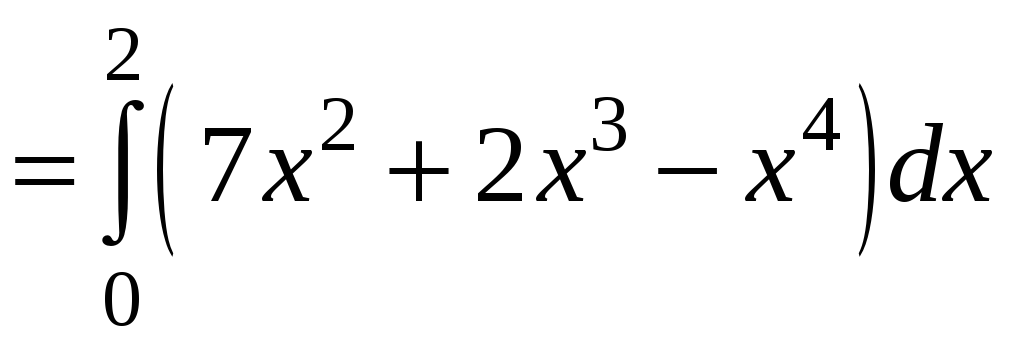
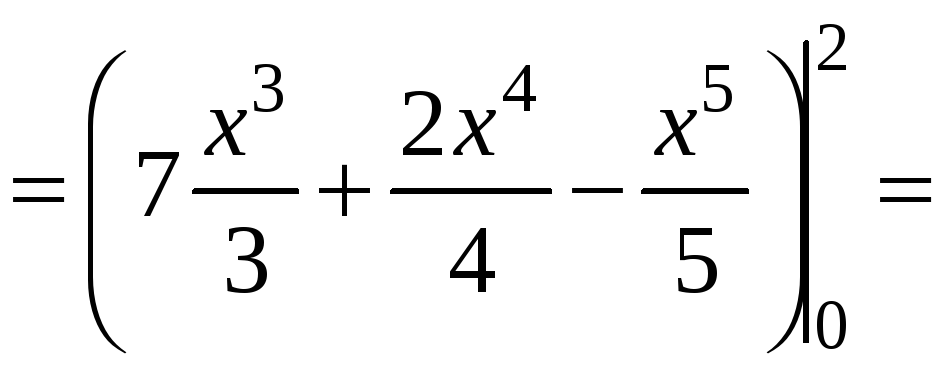
II способ. .

. 

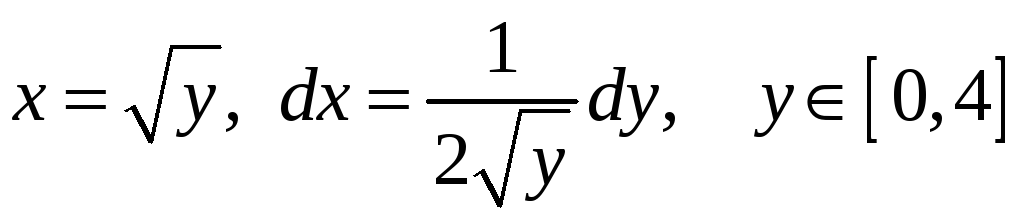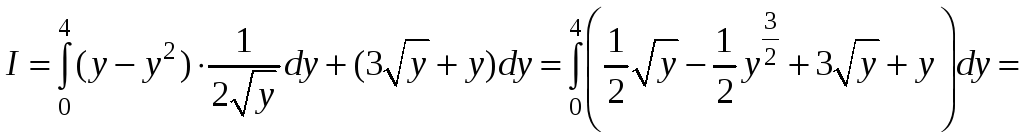
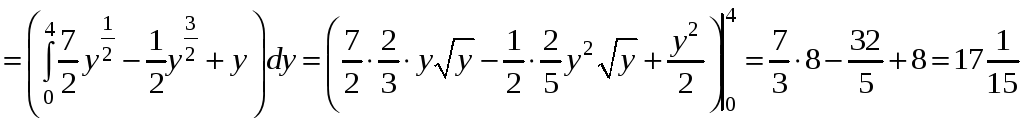Пример 2. , где L - верхняя половина эллипса, 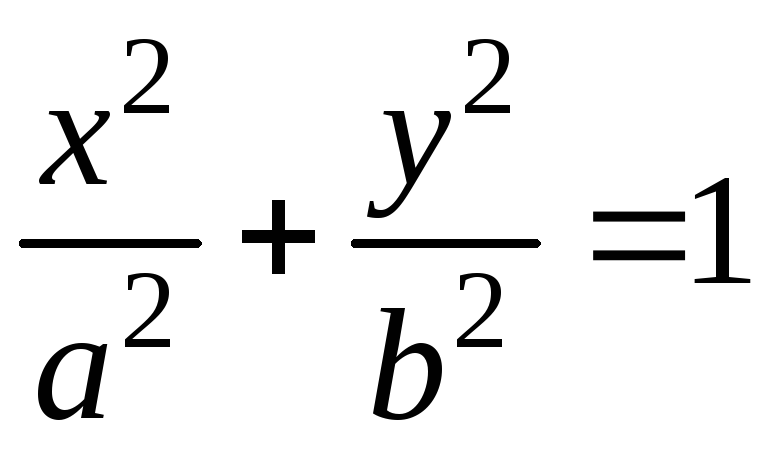, проходимая по часовой стрелке.

Δ 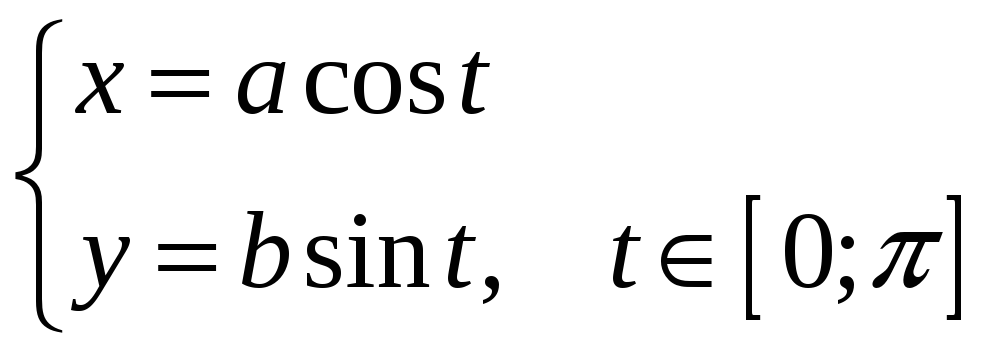- параметрические уравнения кривой L (t изменяется от до 0!)

, .

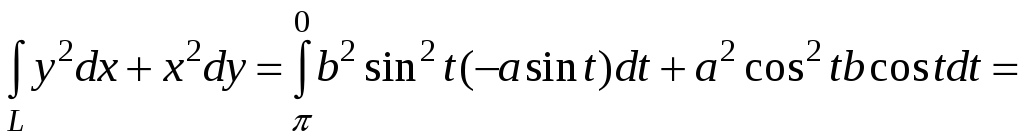
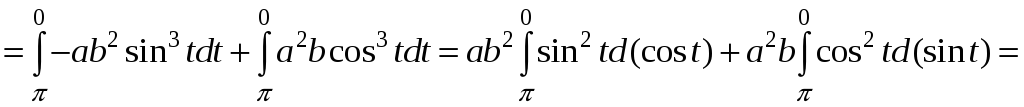
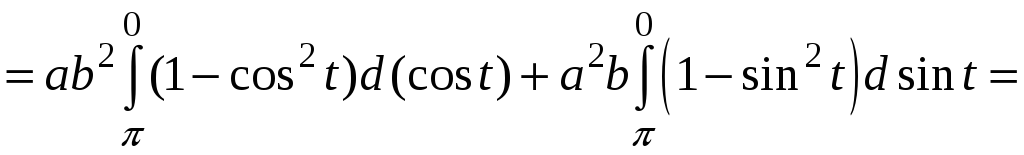
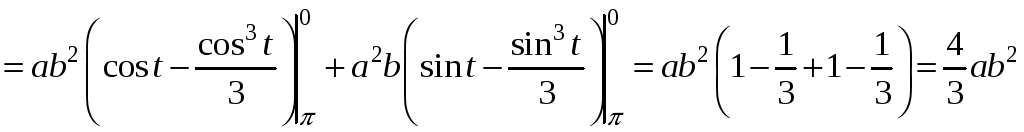. Δ