3. Задача о массе кривой

Рассмотрим физическую задачу, которая приводит к понятию криволинейного интеграла I типа. Пусть вдоль некоторой спрямляемой кривой L распространена масса с плотностью (М) ML.

Задача. Определить массу всей этой кривой.

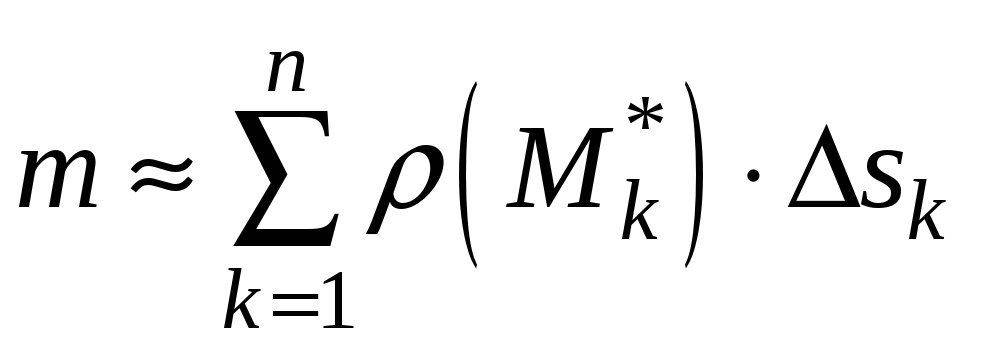Разобьем кривую L на частичные дуги . На каждой частичной дуге выберем произвольно точку , - плотность в точке . Будем считать, что плотность на всей частичной дуге постоянна и равна . Тогда - масса дуги , следовательно, - масса всей кривой L.

Последнее равенство тем точнее, чем меньше разбиение. Пусть . Тогда

.

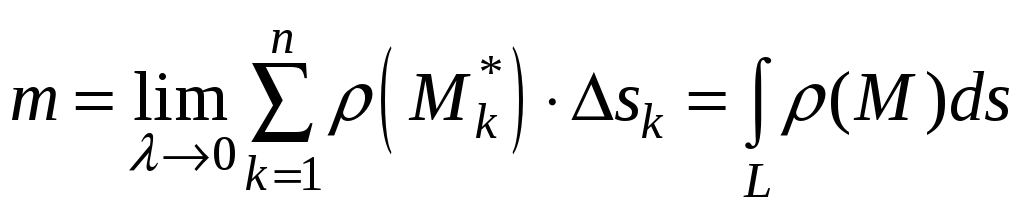Физический смысл криволинейного интеграла I типа

физически выражает массу кривой L, плотность в каждой точке которой равна f(M).

4. Вычисление криволинейного интеграла I типа

Криволинейный интеграл I типа вычисляется путем сведения его к обыкновенному определенному интегралу. Пусть требуется вычислить .

Теорема. Пусть кривая L=AB задана параметрически

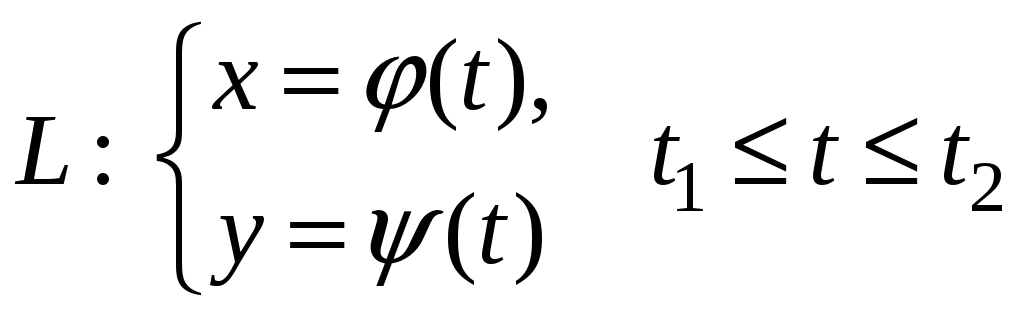, (3)

где (t) и (t) - непрерывно дифференцируемы на [t₁;t₂]. Пусть f(x;y) непрерывна на кривой L. Тогда

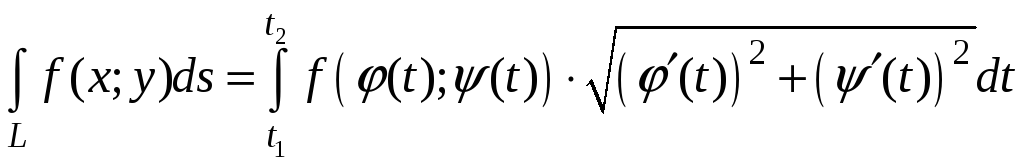. (4)

Доказательство.

Пусть для определенности меньшему значению параметра t₁ соответствует точка A. Функция f(x;y) непрерывна вдоль кривой L, т. е. непрерывна в любой точке М(x;y)L. Положение точки на кривой L определяется длиной дуги . Этим самым координаты x, y точки M тоже определяются как функции от s: 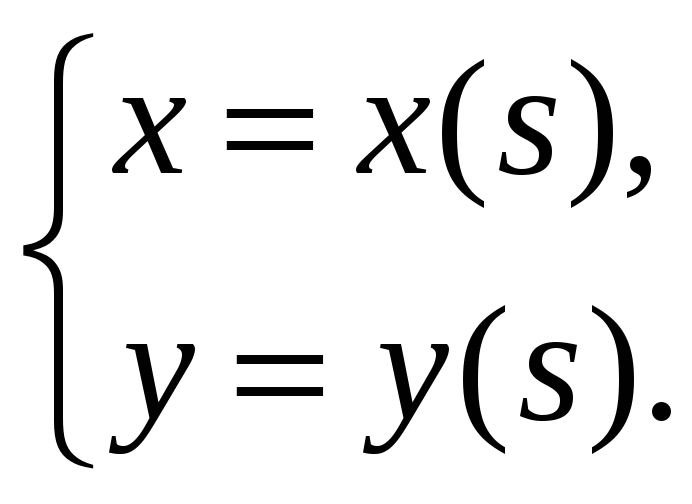Это есть параметрическое представление кривой L с параметром s[0;S], где S - длина всей кривой L. Тогда f(x;y)=f(x(s);y(s))=F(s) - сложная функция от s.

Пусть - произвольное разбиение кривой L на дуги . Произвольно выберем на точку . Обозначим через и значения параметра s, отвечающие соответственно точкам и . Тогда

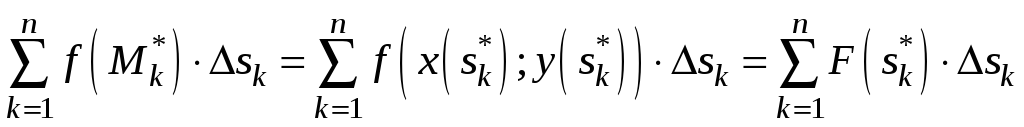. (5)

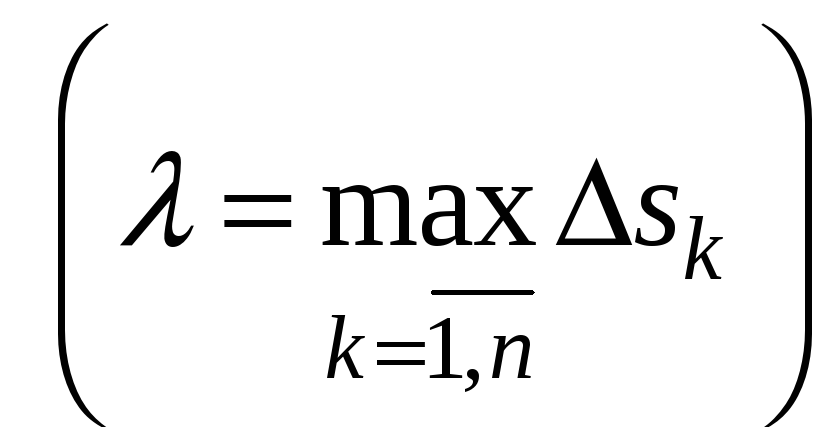Справа в (5) – обычная интегральная сумма для функции F(s), где . Переходя в (5) к , получим

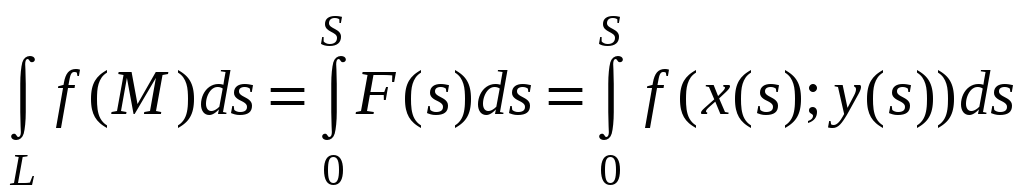, (6)

где интегрирование по s уже обозначает взятие обыкновенного определенного интеграла от функции одной переменной F(s). Так как f(x;y) непрерывна и x=x(s), y=y(s) непрерывны, то сложная функция F(s) непрерывна и, следовательно, существуют все интегралы в (6).

С другой стороны длину s дуги можно рассматривать как функцию параметра t: s=s(t). Таким образом, M=M((t);(t)). С возрастанием t от t₁ до t₂ величина s возрастает от 0 до S. Известно, что дифференциал дуги

.

Выполнив замену переменной в (6) получим:

=.

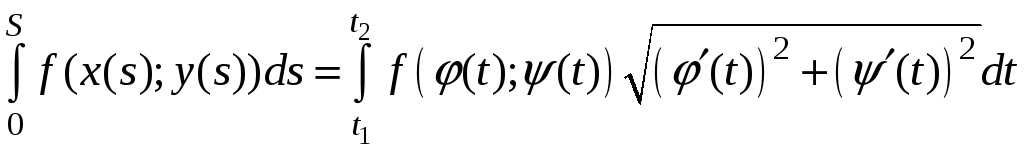Замечание. Если кривая L задана явным уравнением y=(x) (x[a;b], (x)- непрерывно дифференцируемая функция), то принимая за параметр переменную , получим параметрическое уравнение кривой: 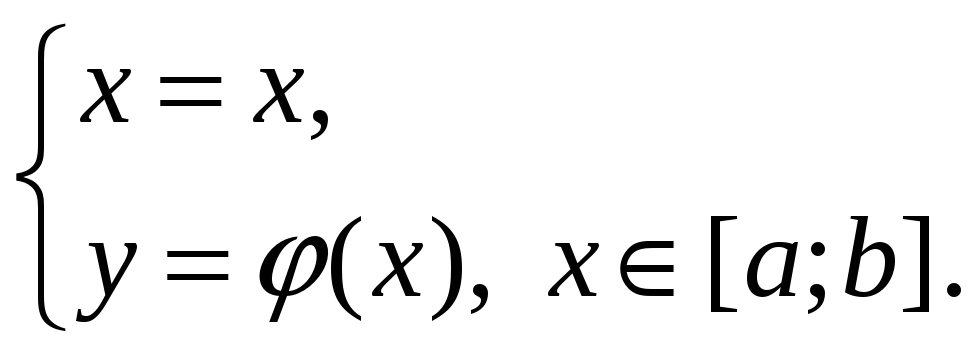Следовательно,

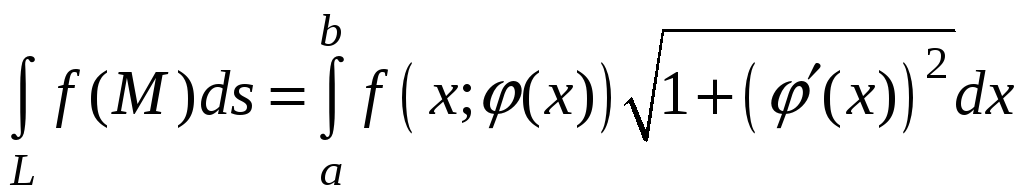. (7)

П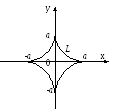ример 1. Вычислить 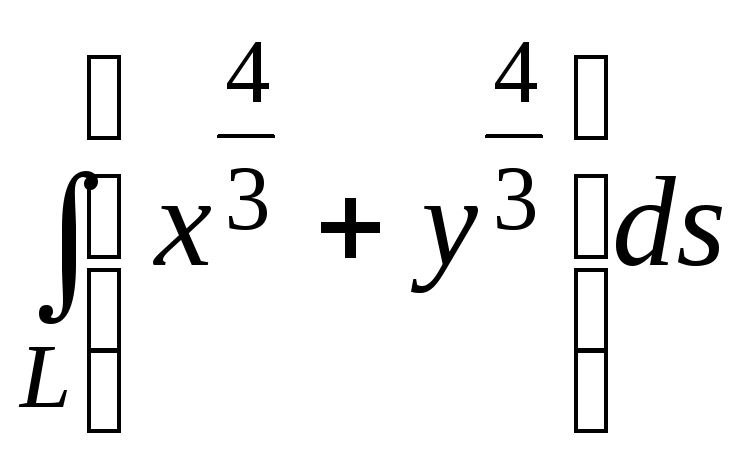, - дуга астроиды , лежащей в первой четверти.

Δ Параметрическое уравнение части астроиды, лежащей в первой четверти:

, .

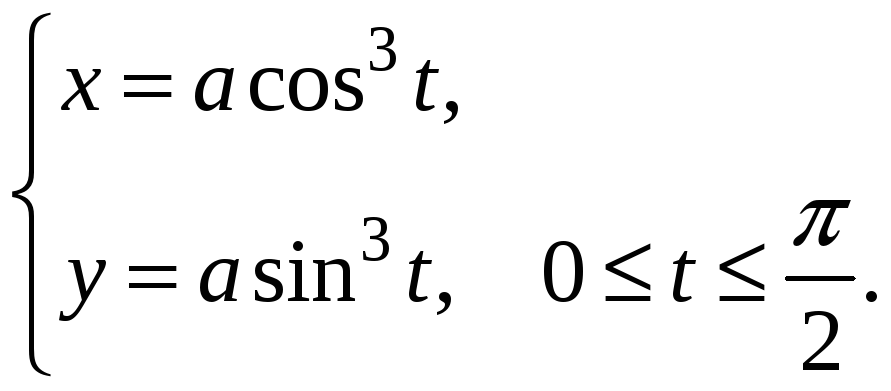
По формуле (4)

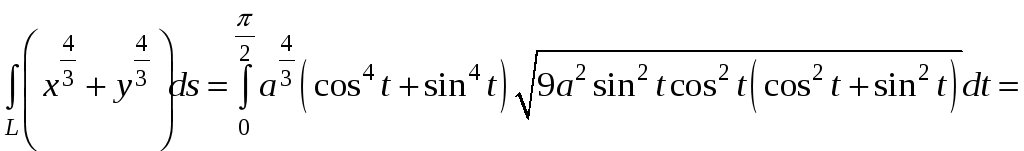
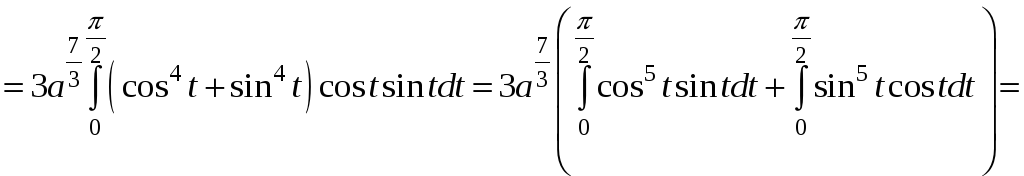
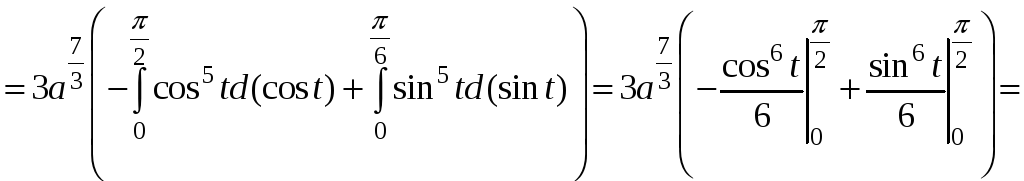
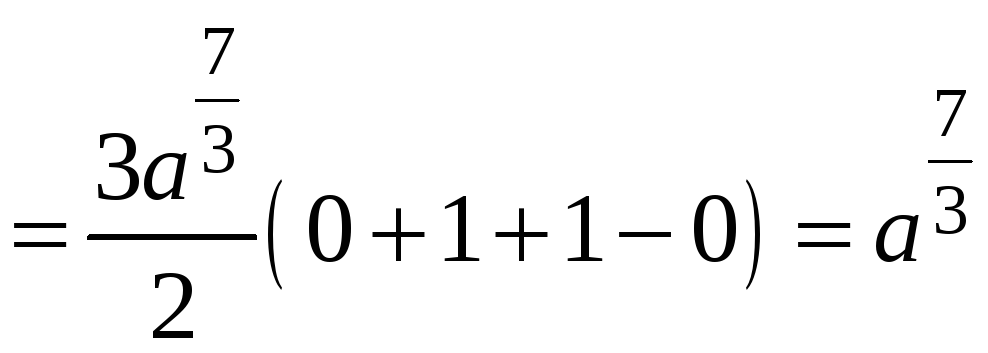. Δ

Пример 2. Вычислить массу всей цепной линии 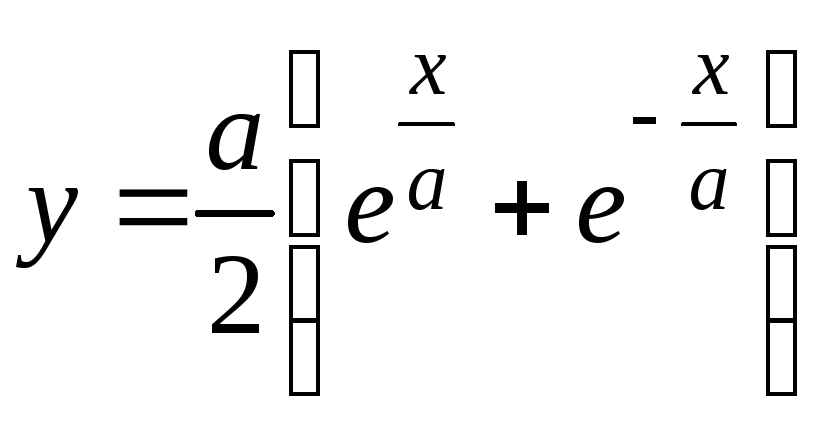, если линейная плотность ее .

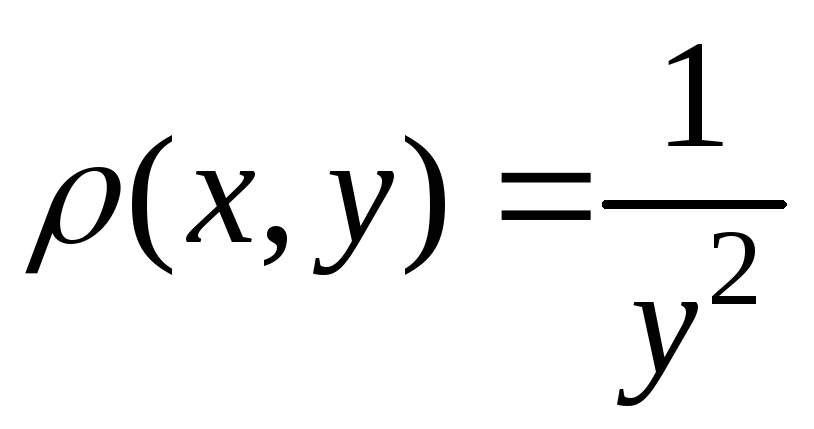Δ . Применим формулу (7):

.

, ,

.

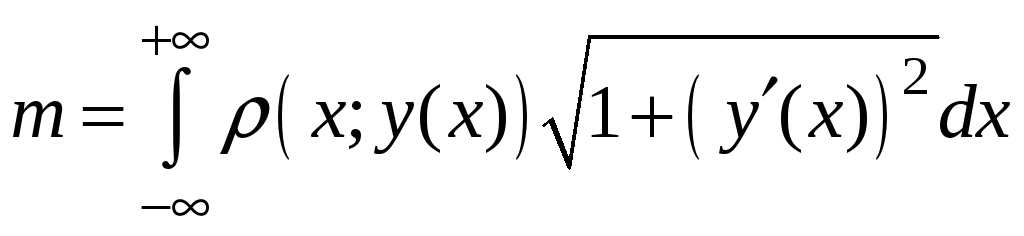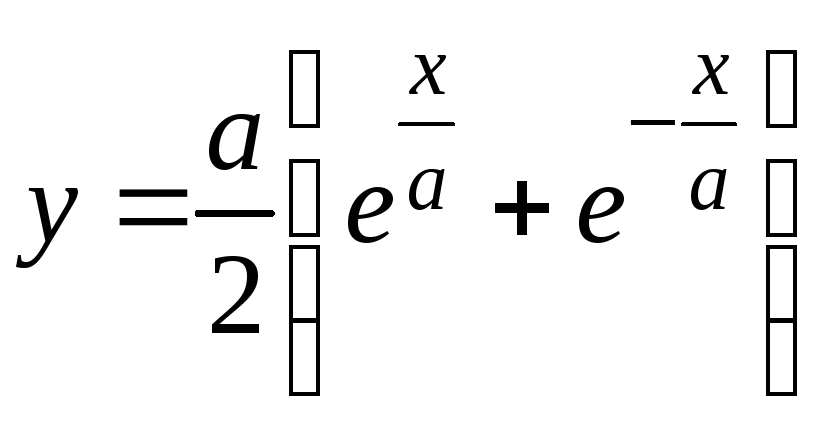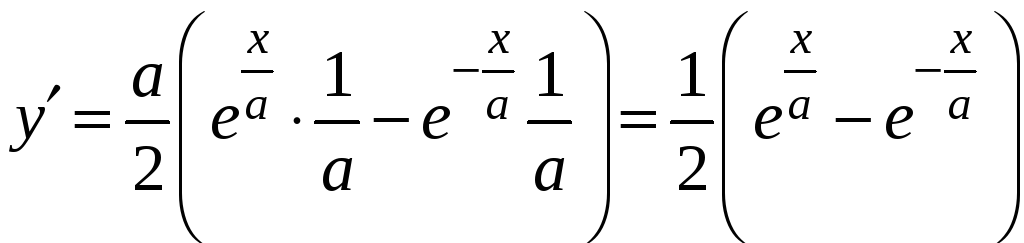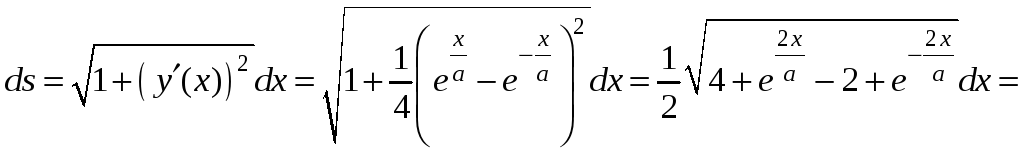
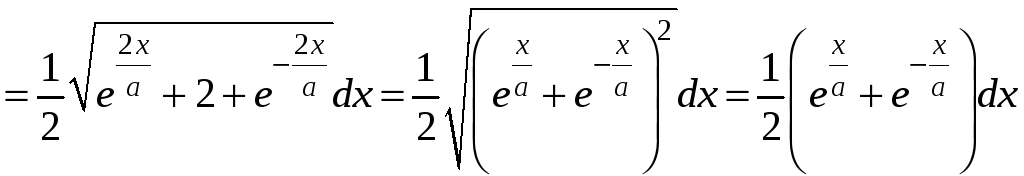Следовательно,

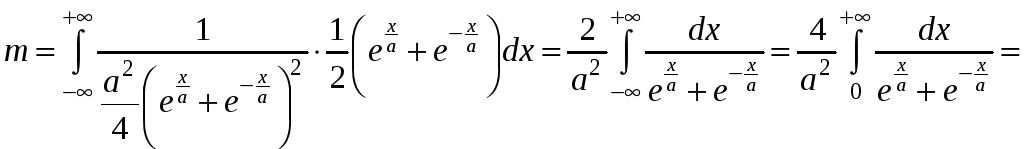
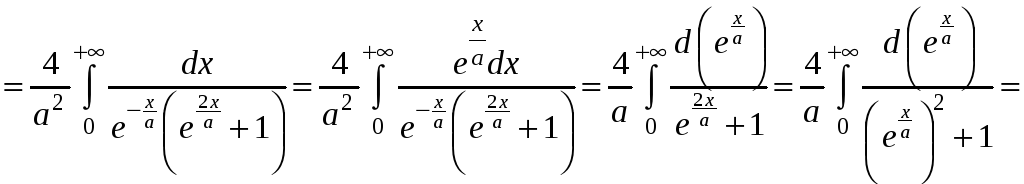
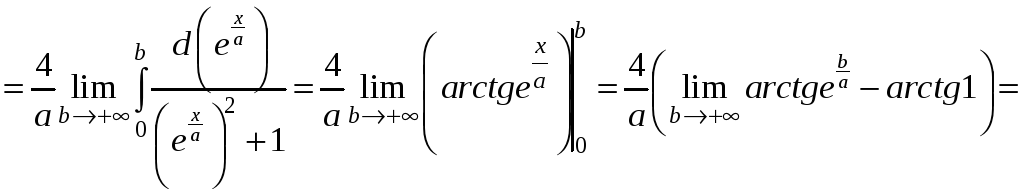
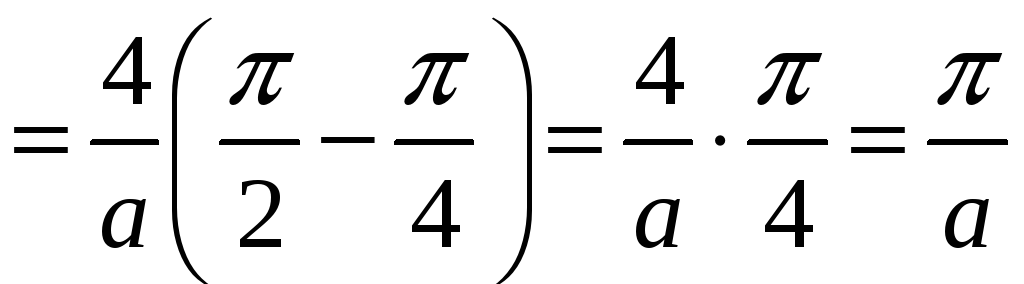. Δ

§2. Криволинейные интегралы II типа

1. Задача о работе плоского силового поля

Пусть материальная точка М, двигаясь прямолинейно под действием постоянной силы совершает перемещение . Работой А, производимой этой силой, называется скалярное произведение вектора силы на вектор перемещения :

.

Если в каждой точке М области (P) определена сила, величина и направление которой зависят только от приложения точки М, то говорят, что на области (P) задано силовое поле.

Пусть материальная точка М движется по кривой ВС, лежащей в области (P) под действием силового поля.

Задача. Определить работу А силового поля при перемещении материальной точки из точки В в точку С по кривой.

Разобьем кривую ВС произвольными точками , взятыми по направлению от В к С, на n частичных дуг. На каждой частичной дуге выберем произвольно точки . На частичной дуге заменим приближенно переменную силу постоянной силой , равной вектору силы в точке . А движение материальной точки по этой дуге заменим ее движением по хорде этой дуги. Выполним это все . В результате приближенных замен имеем:

1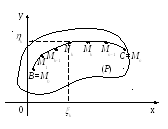) материальная точка движется по ломаной, вписанной в кривую ВС;

2) на каждом звене ломаной на материальную точку действует постоянная сила.

Работа силы на хорде равна

.

Суммируя по , получим

, (1)

- работа ступенчатой силы при движении материальной точки по ломаной , вписанной в кривую ВС. Эту работу считают приближением искомой работы А силы при перемещении материальной точки по кривой ВС: .

Пусть , ,

,

.

Тогда

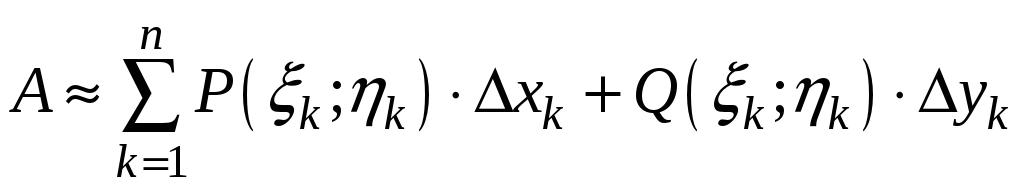. (2)

Пусть - длина , . Переходя в (2) к , получим точное равенство:

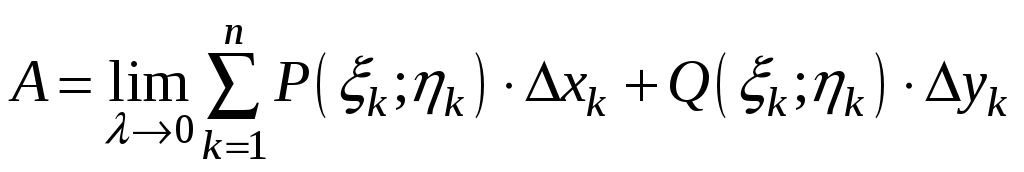. (3)