4. Физический смысл тройного интеграла

Из задачи о массе тела и определения тройного интеграла следует, что если f(x;y;z)0 и непрерывна на (V), то

,

то есть тройной интеграл от неотрицательной непрерывной функции f(x;y;z) выражает массу тела (V), плотность которого в каждой его точке равна f(x;y;z).

5. Условия существования тройного интеграла

Для тройного интеграла аналогично случаю двойного интеграла вводятся понятия нижней и верхней сумм Дарбу:

где , .

Теорема 1 (необходимое и достаточное условие интегрируемости). Для того, чтобы ограниченная функция f(x;y;z) была интегрируема на замкнутой кубируемой области (V), необходимо и достаточно, чтобы .

Теорема 2 (достаточное условие интегрируемости). Всякая непрерывная на замкнутой кубируемой области (V) функция интегрируема на ней.

Теорема 3 (необходимое условие интегрируемости). Если функция f(x;y;z) интегрируема на (V), то она ограничена на (V). (Обратное неверно.)

Свойства тройного интеграла аналогичны свойствам двойного интеграла.

§2. Вычисление тройного интеграла

1. Вычисление тройного интеграла сведением к повторному

Пусть функция f(x;y;z) непрерывна в некоторой области (V). Пусть поверхность (S), ограничивающая тело (V), пересекается не более чем в двух точках любой прямой, параллельной одной из осей координат (например Oz). Более сложные области сводятся к рассматриваемой путем разбиения на части.

Опишем около тела (V) цилиндрическую поверхность с образующей, параллельной оси Oz. Пусть (P_z) - проекция тела (V) на плоскость XOY. Линия касания этой цилиндрической поверхности с поверхностью (S) разбивает (S) на две части: верхнюю и нижнюю. Пусть нижняя часть поверхности задана уравнением z=z₁(x;y), а верхняя – уравнением z=z₂(x;y), где z₁(x;y), z₂(x;y) - однозначные непрерывные функции, заданные на (P_z). Тогда сводится к последовательному взятию внутреннего интеграла по переменной z (при постоянных x и y) и внешнего двойного интеграла по области (P_z):

Предположим теперь, что область (P_z) тоже имеет простую форму, то есть любая прямая, параллельная оси Oy, пересекает контур области (P_z) не более, чем в двух точках. Через a и b обозначим абсциссы самой левой и самой правой точек на контуре области (P_z). Эти точки делят контур на две части, на одной из которых прямые параллельные оси Oy входят в область (P_z), а на другой – выходят. Каждая из этих частей имеет свое уравнение. Первая: y=y₁(x), вторая: y=y₁(x) (axb). В этом случае

,

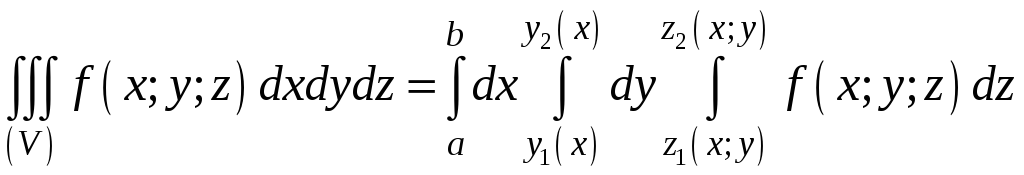то есть тройной интеграл сводится к последовательному вычислению трех определенных интегралов.

Порядок интегрирования может быть другим. Для этого тело (V) надо проектировать на плоскость XOZ или YOZ. Например, спроектируем на XOZ, (Р_у) - проекция на XOZ. Тогда

==

.

Пример 1. Вычислить , где (V) - тетраэдр, ограниченный плоскостями x=0, y=0, z=0 и x+y+z=1.

 Спроектируем тело на плоскость XOY. Проекция P - треугольник со сторонами x=0, y=0, x+y=1. Если x и y – фиксированные, то точка может перемещаться от плоскости z=0 (XOY) до плоскости x+y+z=1. Отсюда z=1-x-y. Итак, если (x;y)(V), то изменяется от 0 до . Следовательно, .

Сведем двойной интеграл к повторному.

Если - фиксировано (0х1) то может изменяться от прямой (ось Ох) до прямой y+x=1 (y=1-x). Следовательно,

. 