13.3. Метод трапеций

 

Этот метод основан на свойствах ВЧХ, следующих из полученной ранее формулы, которые мы рассмотрим без доказательств.

1. Свойство линейности: если ВЧХ можно представить суммой  P() = SPi(), то каждой составляющей Pi() будет соответствовать составляющая переходной характеристики

 

 

,

 

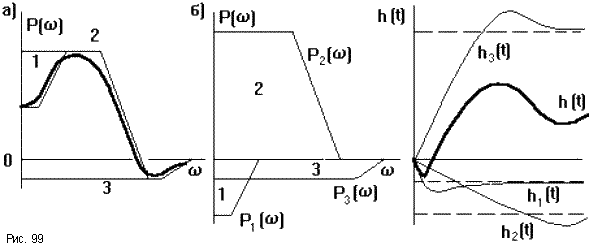
при этом h(t) = (рис.99а). Поэтому, если ВЧХ имеет сложную форму, ее можно представить суммой трапециидальных ВЧХ, примыкающих к вертикальной оси. Затем все трапеции перерисовывают, перенося их основания на горизонтальную ось (рис.99б). Каждой такой трапеции соответствует своя составляющая переходной характеристики h_i(t), имеющая апериодический характер (рис.99в). Р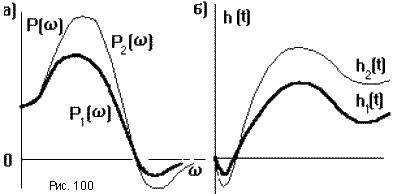езультирующая кривая строится суммированием данных составляющих.

2. Если умножить P() на постоянный множитель а, то соответствующая ей h(t) также умножается на а. То есть, чем выше ВЧХ, тем выше и переходная характеристика (рис.100).

3. Если аргумент w в выражении ВЧХ P() умножить на постоянный множитель а, то аргумент в h(t) будет делиться на это число, то есть

 

.

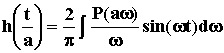
Т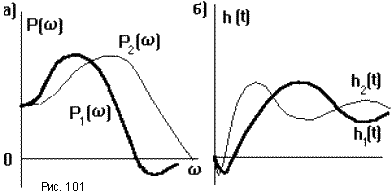о есть переходный процесс в случае P(a) будет протекать в а раз быстрее, чем в случае P() (рис.101).

Рассмотрим трапециидальную ВЧХ (рис.102а). Она характеризуется коэффициентом наклона k = ₁₂. Под единичной трапецией (рис.102б) понимают трапецию, две стороны которой совпадают с осями координат и равны по 1 в соответствующих масштабах; наклон k может быть различным: P₁() = .

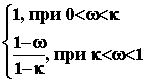П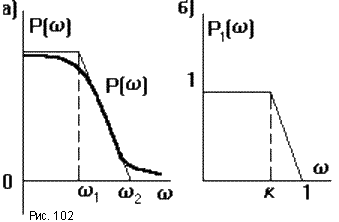одставляя это определение в выражение для определения h(t) можно вычислить кривую переходного процесса, соответствующую единичной трапециидальной ВЧХ. Эти расчеты были проделаны и составлены таблицы h_k -функций.

Для любой трапециидальной ВЧХ, на которые разбита реальная ВЧХ (рис.99б), можно построить подобную ей единичную трапецию со значением k = ₁₂, где ₁ - частота, соответствующая перелому реальной трапеции, ₂ - основание трапеции реальной ВЧХ. Для данной единичной трапеции по таблице h_k-функций строят кривую h_k(k,t), где t - время. Затем, используя свойства 2 и 3 масштабирования ВЧХ и переходной характеристики строят кривую переходного процесса, соответствующего данной трапециидальной ВЧХ. Причем оба описанных процесса можно совместить: сначала задаются моментом времени t, для него по таблице находят значение h_k(k,t), потом умножают это значение на P(0) (масштабирование по вертикальной оси) и откладывают полученное значение на графике h(t) для времени t = t/₂ (масштабирование по горизонтальной оси). Строя таким образом точки для различных моментов времени получают кривую

 

h_i(t/₂) = P(0)h_k(k,t).

 

Данный алгоритм удобно оформить в таблицу:

 

t	hk(k,t)	t = t/2	hi(t) = P(0)hk(k,t)
.....	.....	.....	.....

 

После суммирования составляющих переходного процесса, соответствующих каждой трапеции, получают реальную характеристику h(t).

Описанный метод построения переходной характеристики называется методом трапеций.

 

 

Вопросы

1. Какую частотную характеристику используют для оценки качества управления САУ?

2. Какому значению на переходной характеристике соответствует точка ВЧХ при = 0?

3. Какую форму имеет кривая переходного процесса САУ с вогнутой ВЧХ?

4. Какую форму имеет кривая переходного процесса САУ с трапециидальной ВЧХ?

5. Какую форму имеет кривая переходного процесса САУ с ВЧХ, имеющей экстремум?

6. Как оценить время переходного процесса по виду ВЧХ?

7. В чем состоит метод трапеций?

8. Как используется в методе трапеций свойство линейности?

9. Как изменится кривая переходного процесса, если ВЧХ растянуть вдоль вертикальной оси?

10.  Как изменится кривая переходного процесса, если ВЧХ растянуть вдоль горизонтальной оси?

11.  Что называется единичной трапецией?

12.  Сформулируйте алгоритм построения переходной характеристики в методе трапеций?