
- •Исходные данные:
- •Определение идеального предела мощности удаленной системы
- •1.3. Векторная диаграмма системы I с явнополюсным генератором
- •4.1.Исходный режим
- •4.2. Аварийный режим
- •4.3. Послеаварийный режим
- •Министерство науки и образования Украины Национальный технический университет Украины
- •Расчетно-графическая работа
- •Киев 2011
4.1.Исходный режим
Для анализа динамической устойчивости рассмотрим простейшую систему, работающую через трансформаторы и двухцепную ЛЭП на шины бесконечной мощности (рис.4.1). Схема замещения такой системы представлена на рис.4.2.
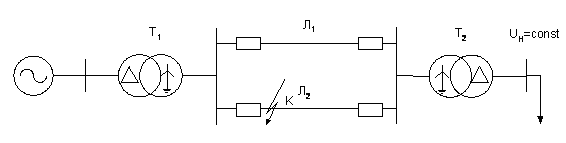
Рис. 4.1 Расчетная схема для анализа динамической устойчивости.
 Рис.4.2. Схема замещения системы в исходном
режиме.
Рис.4.2. Схема замещения системы в исходном
режиме.
До возникновения возмущения исследуемая система является симметричной и работает устойчиво, при этом соблюдается баланс мощности. Электромагнитная мощность простейшей системы (рис.1.2) в исходном режиме равна:
![]() (4.1)
(4.1)
Однако использовать формулу (4.1) для
анализа динамической устойчивости
сложно, так как синхронная ЭДС
![]() в момент возмущения меняется скачком.
в момент возмущения меняется скачком.
Результирующее же потокосцепление
обмотки возбуждения генератора и
определяемая им переходная ЭДС
![]() в момент возмущения не меняются и поэтому
ее можно использовать для характеристики
состояния системы в исходном режиме и
в начальный момент внезапного нарушения
режима.
в момент возмущения не меняются и поэтому
ее можно использовать для характеристики
состояния системы в исходном режиме и
в начальный момент внезапного нарушения
режима.
Переходную ЭДС
![]() и угол
и угол
![]() в
исходном режиме можно получить используя
формулы,
в
исходном режиме можно получить используя
формулы,
приняв
![]() и введя генератор в схему замещения
исходного режима сопротивлением
и введя генератор в схему замещения
исходного режима сопротивлением
![]() :
:
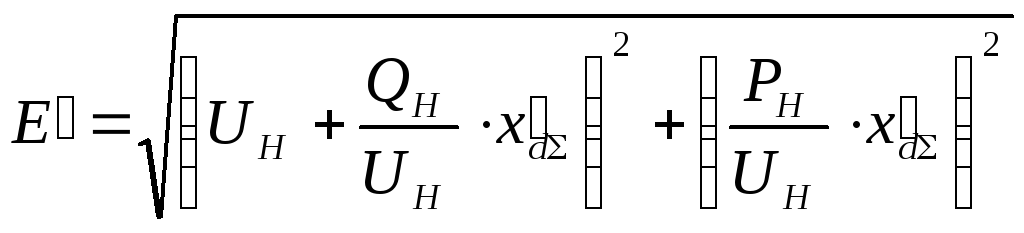 (4.2)
(4.2)
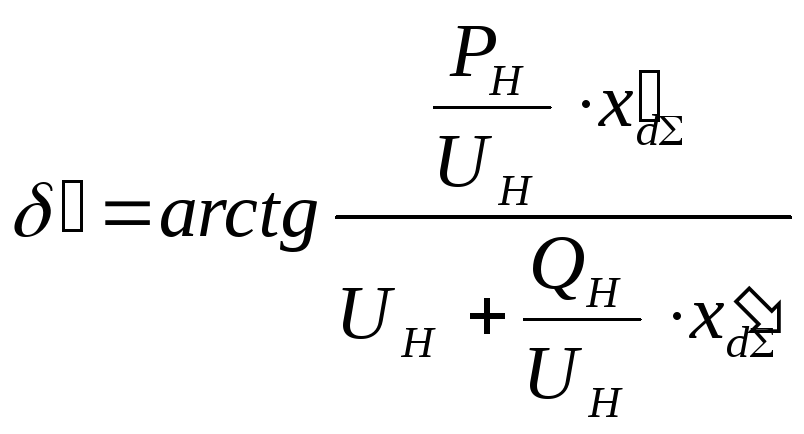
 (4.3)
(4.3)
Подставляя числовые значения в (4.2), (4.3), получим:
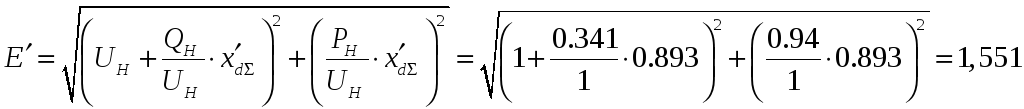
![]()
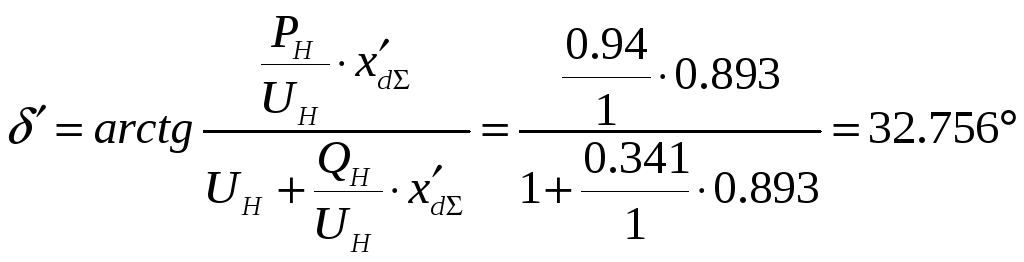
 Здесь
угол
Здесь
угол
![]() между
напряжением в узле нагрузки
между
напряжением в узле нагрузки
![]() и ЭДС
и ЭДС
![]() в дальнейшем будем обозначать δ.
Эквивалентная схема системы в исходном
режиме представлена на рис.4.3
в дальнейшем будем обозначать δ.
Эквивалентная схема системы в исходном
режиме представлена на рис.4.3
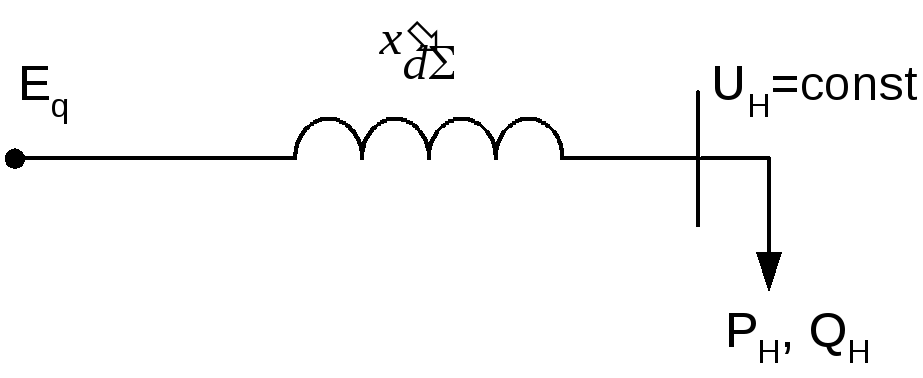
Рис.4.3. Эквивалентная схема системы в исходном режиме.
С учетом принятых допущений выражение для электромагнитной мощности простейшей системы в исходном режиме равно:
![]() (4.4)
(4.4)
На рис.4.3 изображен график зависимости
![]() .
Предел передаваемой мощности в исходном
режиме достигается при
.
Предел передаваемой мощности в исходном
режиме достигается при
![]() и
равен по (4.2):
и
равен по (4.2):
![]()
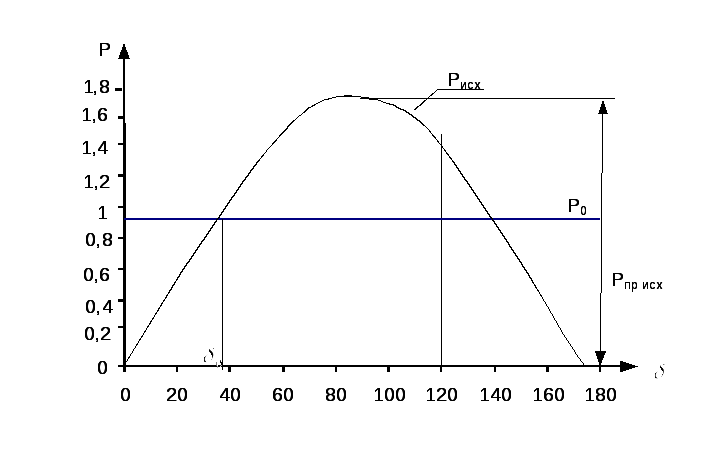
Рис.4.3 График изменения
![]() в функции угла δ.
в функции угла δ.
4.2. Аварийный режим
При анализе динамической устойчивости системы при двухфазном КЗ на землю будем использовать метод симметричных составляющих, при котором несимметричная система рассматривается в виде совокупности симметричных составляющих (прямой, обратной и нулевой последовательности).
Таким образом, при анализе динамической устойчивости при двухфазном КЗ на землю нужно составить схему замещения аварийного режима системы, из которой можно определить токи прямой последовательности и электромагнитную мощность генератора.
Схема замещения в аварийном режиме (рис.4.4) для определения электромагнитной мощности генераторов Раb при двухфазном КЗ на землю отличается от схемы замещения в исходном режиме тем, что в место КЗ в точке а включено эквивалентное шунтирующее сопротивление КЗ ΔХ, равное
![]() ,
(4.3)
,
(4.3)
здесь
![]() сопротивления схемы замещения системы
соответственно токам обратной и нулевой
последовательность относительно место
КЗ.
сопротивления схемы замещения системы
соответственно токам обратной и нулевой
последовательность относительно место
КЗ.
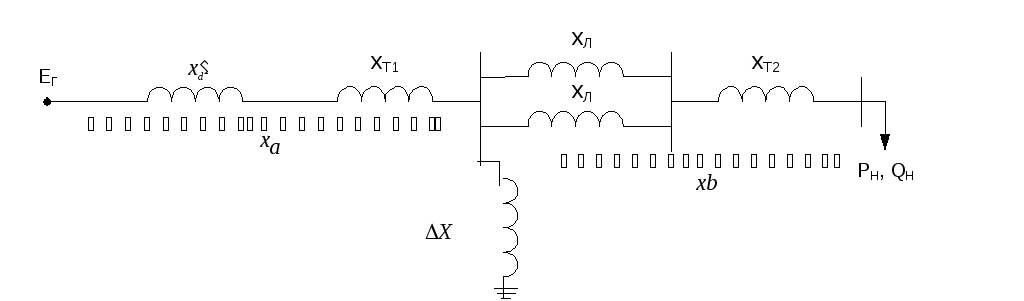
Рис.4.4. Схема замещения системы в аварийном режиме.
При принятых в исходной расчетной схеме системе схемах соединения обмоток трансформаторов можно составить схему замещения обратной (рис.4.5) и нулевой (рис.4.6) последовательностей. Эквивалентные сопротивления относительно места КЗ определяются по формулам:
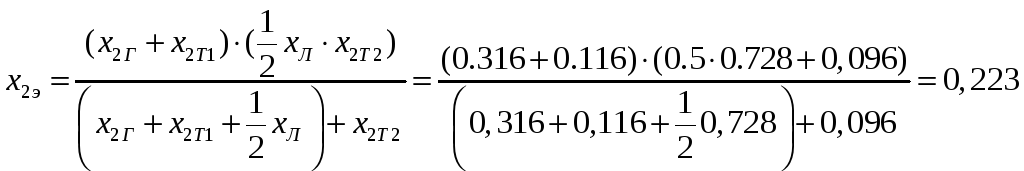 (4.4)
(4.4)
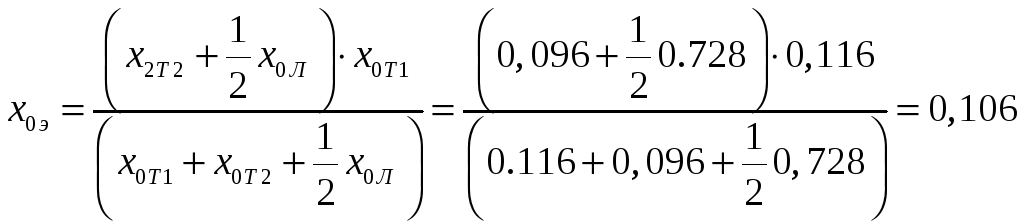 (4.5)
(4.5)
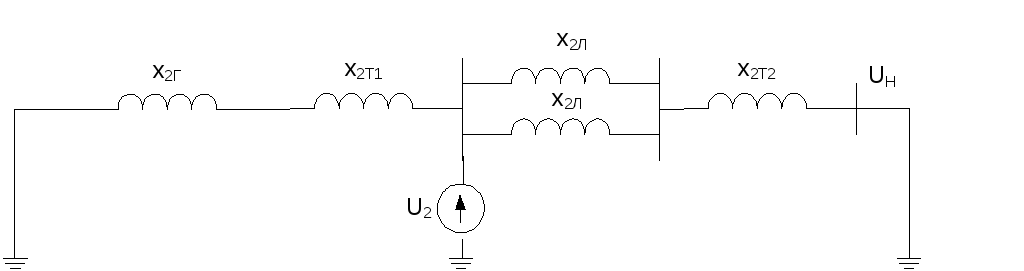
Рис.4.5. Схема замещения обратной последовательности.
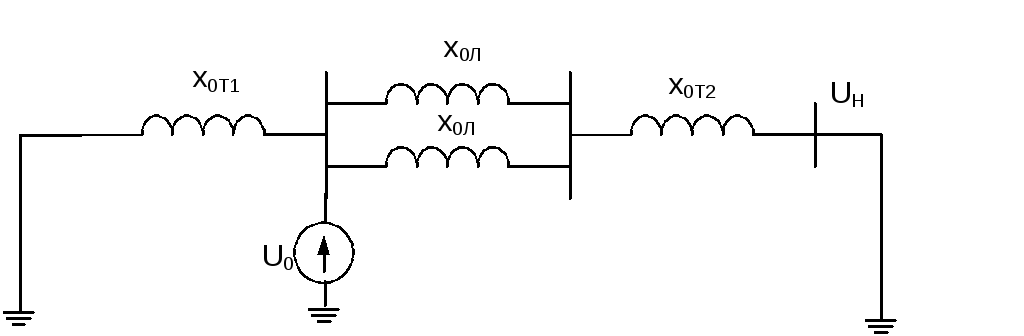
 Рис.4.6.
Схема замещения нулевой последовательности.
Рис.4.6.
Схема замещения нулевой последовательности.
Подставляя в (4.3) найденные значения, получим
![]()
В схеме замещения системы в аварийном
режиме генератор представляется ЭДС![]() за сопротивлением
за сопротивлением
![]() .
Это связано с тем, что по сравнению с
временем протекания переходного процесса
постоянная времени затухания
.
Это связано с тем, что по сравнению с
временем протекания переходного процесса
постоянная времени затухания
![]() имеет значительно большее значение.
имеет значительно большее значение.
Приведем схему (рис.4.4) к трехлучевой
звезде с сопротивлениями
![]() (рис.4.7), где
(рис.4.7), где
![]()
![]()
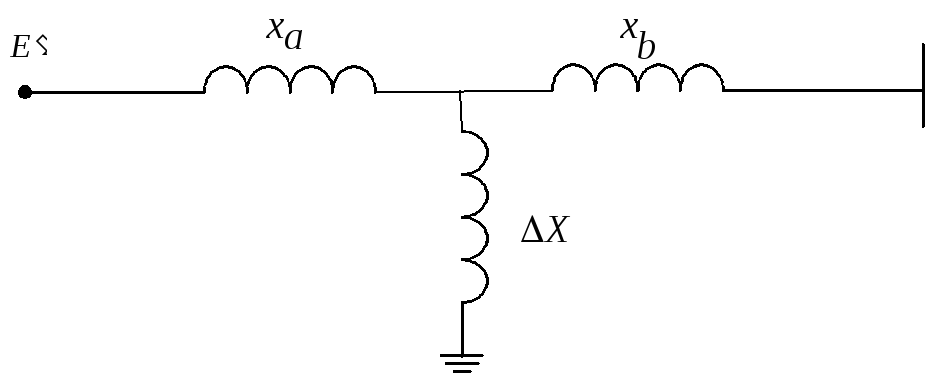
Рис.4.7. Трехлучевая схема замещения системы при КЗ.
Преобразовав звезду в треугольник, получим П-образную схему связи генераторов системы I с шинами неизменного напряжения (рис.4.8):
![]()
![]() (4.6)
(4.6)
![]()
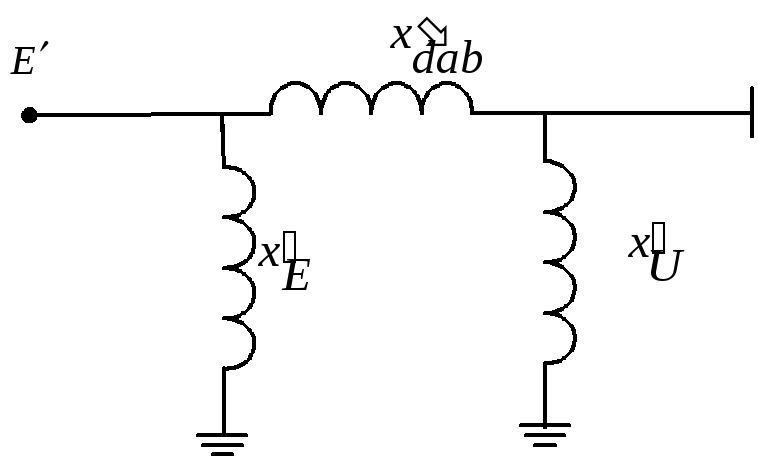
Рис.4.8. П-образная схема замещения системы при КЗ.
В формулах (4.6) сопротивления
![]() не влияют на величину активной мощности
генератора в аварийном режиме и могут
быть отброшены. Следовательно, вся
активная мощность генераторов системы
I направляется к шинам бесконечной
мощности через сопротивление
не влияют на величину активной мощности
генератора в аварийном режиме и могут
быть отброшены. Следовательно, вся
активная мощность генераторов системы
I направляется к шинам бесконечной
мощности через сопротивление
![]() ,
являющимся эквивалентным сопротивлением
системы в ава
,
являющимся эквивалентным сопротивлением
системы в ава рийном
режиме. Выражение для характеристики
электромагнитной мощности в аварийном
режиме будет иметь вид:
рийном
режиме. Выражение для характеристики
электромагнитной мощности в аварийном
режиме будет иметь вид:
![]() ,
,
где предел передаваемой мощности в аварийном режиме
![]()
Так как
![]() <
<![]() ,
то система заведомо неустойчива (рис.4.9)
,
то система заведомо неустойчива (рис.4.9)
