Эффективный портфель

Из всего множества активов в эффективный портфель (граница – линия АВСН) входят такие, которые при заданном уровне риска обеспечивают наибольшую норму доходности или обеспечивают требуемую норму доходности при минимальном риске.

Поскольку, как говорилось выше, отношение каждого инвестора к риску определяется кривыми безразличия, для каждого инвестора может быть выбран оптимальный эффективный портфель.

Кривые безразличия.

Метод, который применяется для выбора наиболее желательного портфеля использует так называемые кривые безразличия инвестора. Эти кривые отражают отношение инвестора к риску и доходности и представляют собой различные комбинации риска и доходности, которые инвестор считает равноценными.

Рис. 5.1. График кривых безразличия инвестора, избегающего риска.

Инвестор будет считать портфели А и В равноценными, несмотря на то, что они имеют различные ожидаемые доходности и стандартные отклонения, так как оба эти портфеля лежат на одной кривой безразличия .

Кривые безразличия не могут пересекаться. Чтобы доказать это условие, предположим, что кривые безразличия пересекаются (рис 5.2).

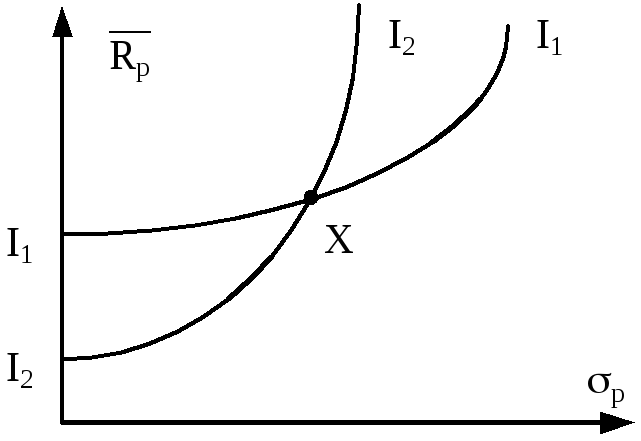
Рис. 5.2. Пересекающиеся кривые безразличия.

На рис. 5.2 точка пересечения обозначена Х. Все портфели на кривой являются равноценными. Это означает что все они также ценны, как и Х, потому что Х находится на . Все портфели на является равноценными и в то же время такими же ценными, как и Х, потому что Х также принадлежит кривой . Исходя из того, что Х принадлежит кривым безразличия, все портфели на должны быть настолько же ценны, насколько и все портфели на . Но это приводит к противоречию, потому что и являются двумя различными кривыми, отражающими различные уровни желательности.

Вернемся к рис 5.1 Инвестор найдет портфель С с ожидаемой доходностью 11 % и стандартным отклонением 14 %, более предпочтительным по сравнению с А и В. Это объясняется тем, что портфель С лежит на кривой безразличия , которая расположена выше и левее, чем .

Это приводит к следующему свойству кривых безразличия:

• инвестор будет считать любой портфель, лежащий на кривой безразличия, которая находится выше и левее, более привлекательным, чем любой портфель, лежащий на кривой безразличия, которая находится ниже и правее.

Инвестор имеет бесконечное число кривых безразличия. Это означает, что как бы не были расположены две кривые безразличия на графике, всегда существует возможность построить третью кривую, лежащую между ними.

При использовании подхода Марковица делается предположение о ненасыщаемости, т.е. предполагается, что инвестор предпочитает более высокий уровень конечного благосостояния более низкому его уровню.

Второе предположение заключается в том, что инвестор избегает риска и, что степень избежания рисков у различных инвесторов неодинакова.

Также можно предположить, что инвестор азартен или нейтрален к риску.

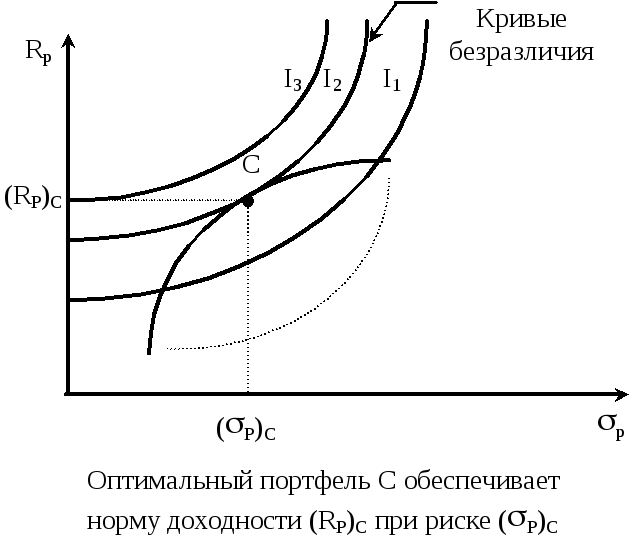
Оптимальный портфель инвестора расположен в точке С, точке касания кривой безразличия инвестора с границей эффективных портфелей.