18. Запишите уравнения Лагранжа II рода. Сколько этих уравнений можно составить для конкретной механической системы.

Уравнения Лагранжа второго рода представляют собой дифференциальные уравнения движения несвободной механической системы в обобщенных координатах.

, ()

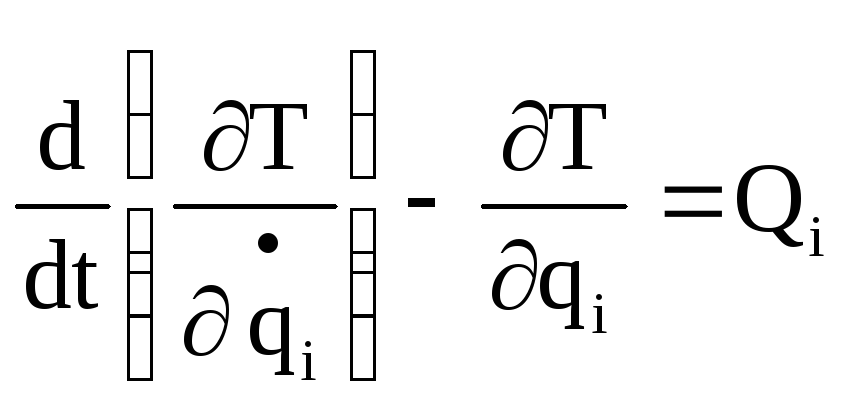3N - число координат у N точек системы в пространстве.

s - количество связей, нахоженных на систему.

n=3N-s - число обобщенных координат определяющих положение системы (если связи наложенные на систему голономные и удерживающие, то n - количество степеней свободы данной системы).

Уравнений для какой-то конкретной задачи составляют ровно столько, сколько степеней свободы имеет рассматриваемая механическая система.

О том, как пользоваться уравнениями Лагранжа II рода при решении задач аналитический динамики читайте в лекциях Харина стр. 151