11. При каких связях действительное перемещение точки совпадает с одним из возможных?

Если связь стационарная, то элементарное действительное перемещение точки совпадает с одним из возможных .

12. Дайте определение и запишите формулу возможной работы силы. Какие связи называются идеальными?

Возможной работой силы называется работа силы на любом возможном перемещении точки ее приложения: .

Возможной работой сил , приложенных к точкам механической системы в данный момент времени, называется работа, которую совершили бы эти силы на возможном перемещении системы:

.

Связи называются идеальными, если возможная работа реакций связей на любом возможном перемещении системы из любого ее положения равна нулю.

13. Сформулируйте определение обобщенной силы. Каково аналитическое выражение обобщенной силы?

()

Скалярную величину называют обобщенной силой, соответствующей i-ой обобщенной координате.

Обобщенной силой, соответствующей некоторой обобщенной координате, называется величина, равная коэффициенту при вариации этой обобщенной координаты в выражении возможной работы всех активных сил, действующих на механическую систему ().

При изменении обобщенных координат, изменяются и обобщенные силы.

Обобщенная координата определяет размерность обобщенной силы.

Аналитический способ вычисления обобщенной силы:

14. Если система находится в потенциальном силовом поле, то как выражаются обобщенные силы через потенциальную энергию?

Если силы приложенные к точкам системы потенциальные:

Потенциальная сила: , поставим в

- частная производная силовой функции по i-ой обобщенной координате.

Тогда: ,

,

то: ,

Если все действующие на систему силы потенциальны, то обобщенные силы равны частным производным от силовой функции по соответствующим обобщенным координатам.

15. Сформулируйте и запишите принцип возможных перемещений для механической системы.

Для равновесия механической системы, на которую наложены голономные, стационарные, удерживающие и идеальные связи, необходимо и достаточно, чтобы сумма работ всех активных сил, приложенных к точкам системы, на любом возможном перемещении системы равнялась нулю.

- равнодействующая активных сил, приложенных к k-ой точке системы.

- вектор возможного перемещения этой точки.

Запишем принцип в следующей форме: () или в проекциях на оси декартовой системы координат: ().

(),() - общие уравнения статики.

16. Как формулируются условия равновесия механической системы в обобщенных координатах.

Условие равновесия голономной системы в обобщенных координатах выглядит так: .

Для равновесия механической системы с голономными, удерживающими, стационарными и идеальными связями необходимо и достаточно, чтобы все обобщенные силы, соответствующие выбранным обобщенным координатам, равнялись нулю.

17. Сформулируйте и запишите общее уравнение динамики в векторной и аналитической формах.

При любом движении механической системы с идеальными и удерживающими связями в каждый данный момент сумма возможных работ всех активных сил и сил инерции на любом возможном перемещении равна нулю.

- общее уравнение динамики.

В проекциях на декартовы оси координат:

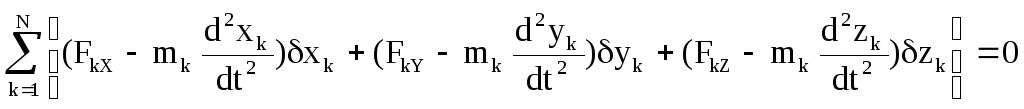
Если связи стационарные, то общее уравнение динамики представляет собой следствие принципа Даламбера и принципа возможных перемещений.