§6. Обратная матрица.

Для квадратной матрицы важную роль играет понятие обратной матрицы.

Определение 1. Матрицей, обратной матрице А (обозначается ), называется матрица, удовлетворяющая условию: .

Теорема 1. Обратная матрица (если она существует) − единственна.

{Пусть у матрицы А есть 2 обратных: В и С. Рассмотрим произведение ВАС:

ВАС = (ВА)С = ЕС = С. С другой стороны ВАС = В(АС) = ВЕ = В. Отсюда В = С}

Для вычисления обратной матрицы необходимо ввести еще несколько понятий.

Легко заметить, что минор (n – 1) − го порядка у квадратной матрицы А_n можно определять, не задавая строки и столбцы, а, указав один элемент , вычеркнуть i−ю строку и j−ый столбец, на пересечении которых он находится. Поэтому минор М_п−1 матрицы А_п обычно обозначают .

Определение 2. Алгебраическим дополнением элемента называется величина .

Из определения детерминанта матрицы A_n сразу следует, что определитель матрицы равен сумме произведений элементов любой строки (столбца) на алгебраические дополнения этой строки (столбца): ………………………………………….(*)

С другой стороны, …………….(**)

Т.е. сумма произведений элементов любой строки (столбца) на алгебраические дополнения другой строки (столбца) равна нулю. {Фактически, мы получаем определитель с двумя одинаковыми строками (столбцами)}

Определение 3. Транспонированная матрица из алгебраических дополнений называется присоединенной матрицей:.

Теорема 2.

{При умножении k −ой строки А на k − ый столбец получается det(A) (*), при умножении на любой другой столбец получается ноль (**) }

Следствие.

Пример. Найти обратную матрицу для . {

.(проверка)}

Замечания. 1. Полезно запомнить, что обратная матрица второго порядка получается из исходной следующим образом: элементы главной диагонали меняются местами, у элементов второй диагонали изменяется знак. Полученная матрица делится на определитель.

2. Обратная матрица может быть получена с помощью элементарных преобразований. Для этого составляется матрица и левая часть элементарными преобразованиями приводится к единичной. При этом матрица Е преобразуется в обратную {б/д}. Последний пример:

;.

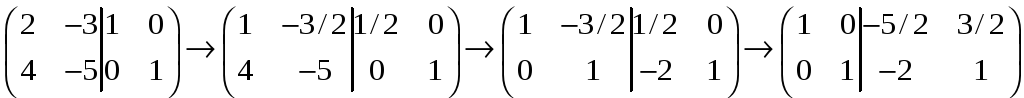Свойства обратной матрицы.

1. { (св.7,8 §3) }

2.

3. {Из определения следует, что А и − взаимно обратные матрицы.}

В заключение докажем критерий существования обратной матрицы:

Теорема 3. Обратная матрица существует тогда и только тогда, когда А − невырожденная матрица, т.е.

{1. Пусть существует. Т.к. она равна присоединенной матрице, деленной на определитель, то последний не равен нулю. 2. Пусть По Сл.Т.2 обратную матрицу можно вычислить.}

§7. Решение матричных уравнений.

Использование обратных матриц позволяет решать простые матричные уравнения относительно квадратных матриц. Рассмотрим пример одной из таких задач. Решить уравнение AXB + C = D, где 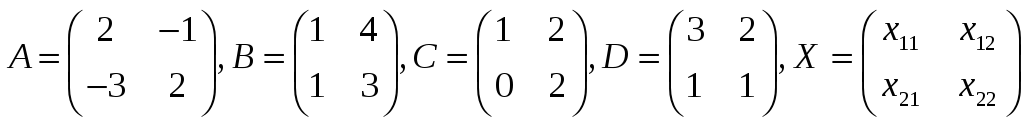− неизвестная матрица.

Матрица Х равна: Пользуясь замечанием 1 предыдущего параграфа, имеем:

Замечание. Так как умножение матриц не коммутативно, необходимо внимательно смотреть за тем, с какой стороны следует умножать правую часть на обратные матрицы.