
- •Порядок выполнения работы
- •Задача о смесях
- •Индивидуальное задание
- •Пример выполнения работы
- •Решение задачи 1а)
- •2. Решение задачи 1 б)
- •Решение задачи 2 а)
- •4. Решение задачи 2 б)
- •Контрольные вопросы
- •Лабораторная работа №2 Целочисленная задача линейного программирования о распиле
- •Краткие теоретические положения
- •Индивидуальное задание
- •Пример выполнения работы
- •Контрольные вопросы
- •Лабораторная работа №3 Классическая транспортная задача
- •Краткие теоретические положения
- •Типы транспортных задач Если суммарные запасы равны суммарным потребностям, т.Е. , то транспортная задача называется закрытой или сбалансированной.
- •Индивидуальное задание
- •Пример выполнения работы
- •Контрольные вопросы
- •Лабораторная работа №4 Решение задач линейного программирования с помощью пакета электронных таблиц exсel
- •Краткие теоретические положения
- •Пример выполнения работы
- •Контрольные вопросы
- •Нахождение оптимальной структуры портфеля ценных бумаг с помощью решения задачи квадратического программирования с использованием пакета excel
- •Краткие теоретические положения
- •Пример выполнения работы
- •Контрольные вопросы
- •Построение математической модели покупательского спроса по статистическим данным
- •Краткие теоретические положения
- •Пример выполнения работы
- •Контрольные вопросы
- •Лабораторная работа №7 Решение задачи о размещении производства с помощью пакета exсel
- •Краткие теоретические сведения
- •Пример выполнения работы
- •Таким образом, изучаемая задача сводится к целочисленной задаче линейного программирования на поиск минимума:
- •Контрольные вопросы
- •Библиографический список
Пример выполнения работы
Пусть Nv=30 – номер варианта, тогда:
![]() ,
,
![]() ,
,
![]() ,
,
![]() -
прибыли от вложения всего капитала в
ценные бумаги соответствующего вида,
где за единицу принят размер вложенного
капитала;
-
прибыли от вложения всего капитала в
ценные бумаги соответствующего вида,
где за единицу принят размер вложенного
капитала;
![]() -минимальная
эффективность вложений;
-минимальная
эффективность вложений;
 - матрица ковариаций.
- матрица ковариаций.
Если
![]() - доли вложения капитала в ценные бумаги,
то матическая модель задачи:
- доли вложения капитала в ценные бумаги,
то матическая модель задачи:

Запустим файл lr5.xls и, вводя значения коэффициентов в ограничениях в таблицу EXCEL, с помощью «Поиска решения» получим следующие результаты:
|
доля t= |
0,13 |
0,54 |
0,33 |
0,00 |
|
Н. гр. |
0 |
0 |
0 |
0 |
|
сумма ti= |
1 |
|
|
|
|
|
Матрица ковариаций |
|||
|
B= |
4,0 |
1,0 |
2,0 |
1,0 |
|
1,0 |
3,0 |
0,5 |
1,5 |
|
|
2,0 |
0,5 |
3,0 |
1,0 |
|
|
1,0 |
1,5 |
1,0 |
3,0 |
|
|
t*B |
1,718 |
1,905 |
1,532 |
1,268 |
|
DR=t*B*tr(t) |
1,755 |
|
|
|
|
|
Эффективности видов бумаг |
|||
|
m= |
2 |
3 |
1 |
3 |
|
|
средняя эффективность |
Условие |
минимальная эффективность |
|
|
MR=t*tr(m)= |
2,20 |
=> |
2,2 |
|
Имеем: t1=0,13; t2=0,54; t3=0,33; t4=0, следовательно, в ценные бумаги 1-го типа вкладывается 13% всех инвестиций, 2-го типа – 54%, 3-го типа – 33%, в ценные бумаги 4-го типа вкладывать деньги нецелесообразно.
Mr=2,20 - математическое ожидание (прибыль от вложения капитала).
Если 100 тыс. руб.
можно вложить на 40 лет в ценные бумаги
4-х видов, то в ценные бумаги 1-го вида
вложим 13 тыс. руб., в ценные бумаги 2-го
вида – 54 тыс. руб., 3-го – 33 тыс. руб., в
ценные бумаги 4-го вида деньги не
вкладываем.
![]() ,755
- дисперсия.
,755
- дисперсия.
В нашем случае Ф(0,95)=0,329 - значение интегральной функции Лапласа. Тогда, с вероятностью Р=0,95 можно утверждать, что размер полученной прибыли при рассчитанных долях вложения капитала, лежит в пределах:
![]()
Т. е. с вероятностью 95% можно утверждать, что по прошествии 40 лет размер полученной от инвестиций прибыли будет лежать в пределах от 176,4 тыс. до 263,6 тыс. руб.
Контрольные вопросы
1. Как математически описывается структура портфеля ценных бумаг?
2. Как определяется
случайная величина ожидаемой прибыли
![]() для заданного портфеля инвестиций, как
рассчитываются ее числовые характеристики:
математическое ожидание и дисперсия?
для заданного портфеля инвестиций, как
рассчитываются ее числовые характеристики:
математическое ожидание и дисперсия?
3. Предположим,
инвестор имеет возможность вложить
долю
![]() капитала в сферу с гарантированной (но
относительно малой) отдачей
капитала в сферу с гарантированной (но
относительно малой) отдачей
![]() .
Сформулировать модель оптимизации в
данном случае.
.
Сформулировать модель оптимизации в
данном случае.
4. Какую структуру имеет каноническая задача квадратического программирования с линейными ограничениями?
5. Как находится доверительный интервал с уровнем доверия P для нормально - распределенной случайной величины, если известны ее математическое ожидание и дисперсия?
ПРИЛОЖЕНИЕ
Таблица 1.
-
Nv
Задание
Nv
Задание
1


2



3


4



5


6



7


8



-
Nv
Задание
Nv
Задание
9


10


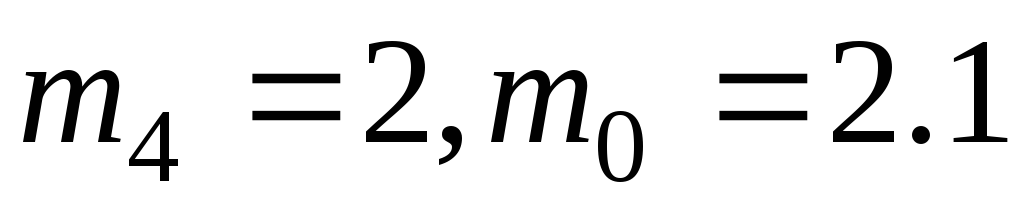
11


12



13


14



15


16



-
Nv
Задание
Nv
Задание
17


18



19

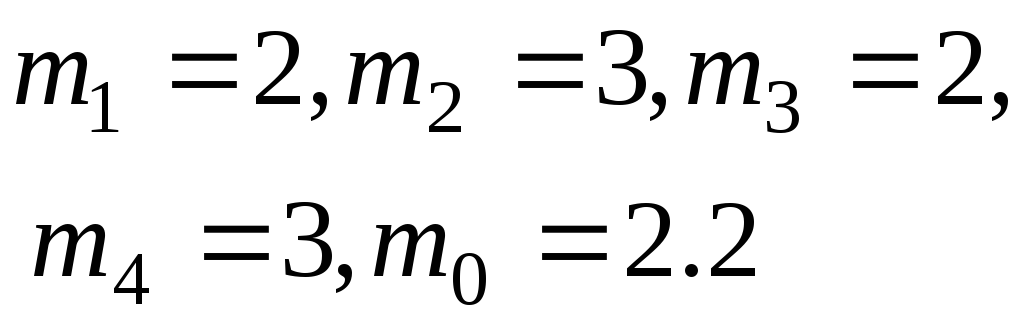
20



21


22



23


24



-
Nv
Задание
Nv
Задание
25


26



27


28



29


30



Лабораторная работа №6
