Пример выполнения работы

Задача1а. Пусть Nv=30, тогда по номеру варианта из таблицы1 приложений:

с₁=2, с₂=3, с₃=2, с₄=1, с₅=4 – прибыль от реализации 1 ед. продукции;

b₁=100, b₂=150, b₃=250, b₄=100 – запасы ресурсов.

По номеру варианта из приложений выпишем технологическую матрицу производства (затраты каждого ресурса для производства 1 ед. каждого продукта):

.

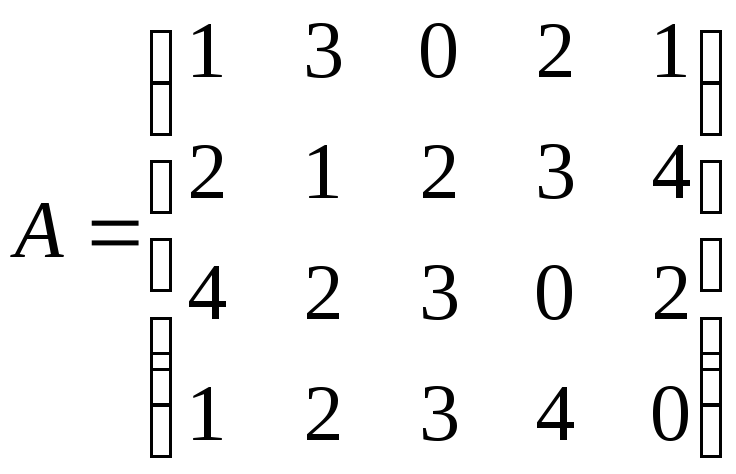Запишем математическую модель задачи:

z max;

1x₁+3x₂+2x₄+1x₅ 100 – ограничение на запасы I ресурса;

2x₁+1x₂+2x₃+3x₄+4x₅ 150 – ограничение на запасы II ресурса;

4x₁+2x₂+3x₃+2x₅250 – ограничение на запасы III ресурса;

1x₁+2x₂+3x₃+4x₄ 100 - ограничение на запасы IV ресурса;

x₁, x₂, x₃, x₄0;

x₁, x₂, x₃, x₄-целые.

Формируем лист исходных данных, работая в пакете “Exсel ”, структура такого листа показана в таблице:

A B C D E F G I J

переменая	X1	X2	X3	X4	X5		max
значение
ниж.граница	0	0	0	0	0
верх. граница						z
целевая ф-ия	2	3	2	1	4
	цел.	цел.	цел.	цел.	цел.
	Ограничения					лев. части	знак	прав. части
I ресурс	1	3	0	2	1		<=	100
II ресурс	2	1	2	3	4		<=	150
III ресурс	4	2	3	0	2		<=	250
IV ресурс	1	2	3	4	0		<=	100

В клетки G8-G11 и G5 указанной таблицы вводятся не числа, а функции Exсel СУММПРОИЗВ, описывающие левые части ограничений задачи ЛП и целевую функцию z. Например, в ячейку G8 введем СУММПРОИЗВ(B2:F2;B8:F8), т.е. в эту ячейку заносится расход 1-го ресурса (аналогично заполняем клетки G9-G11). В ячейку G5 запишем значение целевой функции (получаемая прибыль) СУММПРОИЗВ (B2:F2;B5:F5). Позиции в строке “знач.” не заполняем, в процессе работы программы оптимизации в эти позиции будут занесены оптимальные значения переменных. Далее, вызываем в пункте меню “Сервис” команду “Поиск решения”, вводим тип задачи- поиск максимума, область поиска- ячейки B2-F2, т.е. диапазон ячеек, в которых находятся варьируемые переменные. Вводим все ограничения задачи, в данном случае они будут иметь вид: B3<=B2; C3<=C2; D3<=D2; E3<=E2; F3<=F2- данные ограничения означают неотрицательность переменных; G8<=J8; G9<=J9; G10<=J10; G11<=J11- данные ограничения соответствуют линейным ограничениям задачи ЛП, устанавливаем ячейку, где находятся значения целевой функции, в данном случае G5 и запускаем программу оптимизации на выполнение. После получения сообщения о том, что оптимальное решение найдено, подтверждаем необходимость формирования листа отчета по результатам и выписываем с экрана лист 1, где в ячейках содержатся окончательные значения переменных и лист отчета по результатам. При решении данной задачи получаем измененную таблицу исходных данных, содержащую, окончательные, оптимальные значения переменных:

A B C D E F G I J

переменая	X1	X2	X3	X4	X5		max
значение	1	32	8		25
ниж.граница	0	0	0	0	0
верх. граница						z
целевая ф-ия	2	3	2	1	4	214
	цел.	цел.	цел.	цел.	цел.
	Ограничения					лев. части	знак	прав. части
I ресурс	1	3	0	2	1	97	<=	100
II ресурс	2	1	2	3	4	150	<=	150
III ресурс	4	2	3	0	2	142	<=	250
IV ресурс	1	2	3	4	0	89	<=	100

В сводной форме данные результаты отражены в листе результатов расчета:

Ячейка	Имя	Исходно	Результат
$B$2	знач. x1	0	1
$C$2	знач. x2	0	32
$D$2	знач. x3	0	8
$E$2	знач. x4	0	0
$F$2	знач. x5	0	25
$G$5	цел. Ф. z	0	214

Примечание: знак «$» - абсолютный адрес ячейки (при копировании формулы не изменяется).

Следовательно, необходимо выпускать 1-го продукта 1ед., 2-го – 32 ед., 3-го – 8 ед., 5-го - 25 ед., 4-й продукт не выпускать, и при этом будет достигнута max прибыль в размере 214 руб.

Остатки ресурсов: I рес. – 3 ед., II рес. расходуется полностью, III рес. – 108 ед., IV рес., - 11 ед.

В следующей таблице показан анализ выполнения ограничений задачи ЛП на оптимальном решении, при этом ограничение называется связанным, если оно выполняется как равенство.

Ячейка	Имя	Значение	Формула	Состояние	Разница
$B$3	н.гр. x1	0	$B$3<=$B$2	не связанное	1
$C$3	н.гр. x2	0	$C$3<=$C$2	не связанное	32
$D$3	н.гр. x3	0	$D$3<=$D$2	не связанное	8
$E$3	н.гр. x4	0	$E$3<=$E$2	связанное	0
$F$3	н.гр. x5	0	$F$3<=$F$2	не связанное	25
$G$8	Ограничение 1.	97	$G$8<=$J$8	не связанное	3
$G$9	Ограничение 2.	150	$G$9<=$J$9	связанное	0
$G$10	Ограничение 3.	142	$G$10<=$J$10	не связанное	108
$G$11	Ограничение 4.	89	$G$11<=$J$11	не связанное	11
$B$2	знач. x1	1	$B$2=целое	связанное	0
$C$2	знач. x2	32	$C$2=целое	связанное	0
$D$2	знач. x3	8	$D$2=целое	связанное	0
$E$2	знач. x4	0	$E$2=целое	связанное	0
$F$2	знач. X5	25	$E$2=целое	связанное	0

Задача1б. Выбрать самостоятельно верхнюю границу производства одного из продуктов. Например, V продукт должен производиться в объеме не более 10 единиц.

Математическая модель задачи:

z max;

1x₁+3x₂+2x₄+1x₅ 100 – ограничение на запасы I ресурса;

2x₁+1x₂+2x₃+3x₄+4x₅ 150 – ограничение на запасы II ресурса;

4x₁+2x₂+3x₃+2x₅250 – ограничение на запасы III ресурса;

1x₁+2x₂+3x₃+4x₄ 100 - ограничение на запасы IV ресурса;

x₅ 10 – ограничение на производство Vпродукта;

x₁, x₂, x₃, x₄0;

x₁, x₂, x₃, x₄-целые.

Вводим в ячейку $F$3 10, запускаем «Поиск решения», добавляем ограничение $F$2<= $F$3 и запускаем на выполнение.