
- •Производная. Определение, непрерывность функции, имеющей производную.
- •Геометрический смысл производной.
- •Арифметические свойства производной.
- •Производная обратной функции.
- •Производная сложной функции.
- •Производные элементарных функций.
- •Билет 7 Дифференциал функции. Определение. Геометрический смысл.
- •Необходимое и достаточное условие дифференцируемости.
- •Теорема 1: Для того, чтобы функция была дифференцируемой в точке , необходимо и достаточно , чтобы она имела конечную производную в этой точке.
- •Производные высших порядков. Формула Лейбница.
- •Дифференциалы высших порядков. Инвариантность формы первого дифференциала. Неинвариантность формы дифференциалов второго и высших порядков.
- •Возрастание (убывание) функции в точке. Необходимое и достаточное условие. Теорема Ферма.
- •Теорема Ролля.
- •Теорема Коши. Физический смысл.
- •Теорема о среднем Лагранжа.
- •Достаточное условие невозрастания (неубывания) функции на отрезке. Условие постоянства функции на отрезке.
- •Достаточные условия экстремума.
- •Формула Тейлора для многочленов.
- •Формула Тейлора для дифференцируемых функций.
- •Формула Тейлора для важнейших элементарных функций.
- •Билет 20 Выпуклость функции в точке. Достаточное условие.
- •Теорема 1 (Достаточное условие существования точки перегиба).
- •Непрерывна в и . Тогда, если - нечетное число, то кривая обращена выпуклостью вверх или вниз в зависимости от того, будет ли или, а если четное, то есть точка перегиба кривой.
- •Выпуклость функции на отрезке. Необходимое и достаточное условие.
- •Правило Лопиталя. Случай 0/0.
- •Правило Лопиталя. Случай .
- •Раскрытие неопределенностей вида , ,,, .
- •Асимптота. Уравнение наклонной асимптоты.
- •Первообрáзная. Неопределенный интеграл. Свойства.
- •Замена переменной в неопределенном интеграле.
- •Интегрирование по частям неопределенного интеграла.
- •Интегрирование простейших рациональных дробей
- •Интегрирование рациональных дробей.
- •Интегрирование выражений вида.
- •Первая подстановка Эйлера (Леонарда)
- •Интегрирование тригонометрических выражений.
- •Тригонометрические подстановки.
- •Определенный интеграл Римана. Эквивалентные определения. Условие Коши.
- •Ограниченность интегрируемой функции.
- •Суммы Дарбу. Их Свойства.
- •Суммы Дарбу и интегрируемость функции по Риману.
- •Билет 41 Основная теорема о существовании определенного интеграла Римана.
- •Равномерная непрерывность функции. Модуль непрерывности.
- •Теорема 2 Функция непрерывная на отрезке, равномерно непрерывна на нем ().
- •Интегрируемость по Риману непрерывной функции.
- •Интегрируемость по Риману монотонной функции.
- •Аддитивное и однородные свойства определенного интеграла Римана.
- •Неравенства для определенного интеграла Римана и теорема о среднем.
- •Интеграл как функция верхнего предела. Непрерывность и дифференцируемость. Теорема Ньютона-Лейбница.
- •Билет 48 Определение площади. Площадь криволинейной трапеции. Площадь в полярных координатах.
- •Определение объёма. Объем тела вращения.
- •Длина дуги кривой. Определение и вычисление.
Выпуклость функции на отрезке. Необходимое и достаточное условие.
Определение:
По
определению кривая
![]() называется выпуклой вниз (вверх) на
отрезке [a,b],
если любая дуга этой кривой с концами
в точках
называется выпуклой вниз (вверх) на
отрезке [a,b],
если любая дуга этой кривой с концами
в точках![]() (
(![]() )
расположена
не ниже (не выше) стягивающей ее хорды.
)
расположена
не ниже (не выше) стягивающей ее хорды.
Определение: Множество называется выпуклым, если для любых двух точек этого множества, отрезок, соединяющий их лежит также в этом множестве.
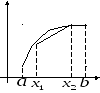


Выпуклость вверх Выпуклое множество
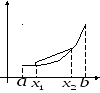

Выпуклость вниз Невыпуклое множество
Теорема 1 (необходимое и достаточное условие выпуклости на отрезке)
Пусть функция
![]() непрерывна на [a,b]
и имеет вторую производную на (a,b).
Для того чтобы кривая
непрерывна на [a,b]
и имеет вторую производную на (a,b).
Для того чтобы кривая
![]() была выпуклой кверху (книзу) на [а,b],
необходимо и достаточно, чтобы выполнялось
неравенство
была выпуклой кверху (книзу) на [а,b],
необходимо и достаточно, чтобы выполнялось
неравенство
![]() (
(![]() )
для всех
)
для всех
![]() .
.
Доказательство:
Пусть наша кривая
выпукла кверху на [a,b].
Тогда для любых х и h
>0 таких, что х, х+2h![]() [a,b],
имеет место неравенство
[a,b],
имеет место неравенство
![]() ,
откуда
,
откуда
![]() .
.
Если теперь
![]() и
и
![]() - произвольные точки интервала (a,b),
то, положив h
= (
- произвольные точки интервала (a,b),
то, положив h
= (![]() -
-
![]() )/n,
будем иметь
)/n,
будем иметь
![]() .
.
Таким образом, (![]() ,
и, переходя к пределу при
,
и, переходя к пределу при
![]() ,
получим неравенство
,
получим неравенство
![]() ,
показывающее, что производная
,
показывающее, что производная
![]() на интервале (a,b)
не возрастает. Но тогда
на интервале (a,b)
не возрастает. Но тогда
![]() на (a,b).
на (a,b).
Обратно, пусть
![]() и
и
![]() .
Нам нужно доказать, что функция
.
Нам нужно доказать, что функция
![]() ,
где
,
где
![]() ,
удовлетворяет неравенству
,
удовлетворяет неравенству
![]() .
Допустим, что это не так. Тогда
.
Допустим, что это не так. Тогда
![]() .
Поэтому
.
Поэтому
![]() .
.
Применяя формулу Тейлора, получим
0=![]() .
Но в правой части этой цепочки равенств
первый член по предположению отрицательный,
а второй неположительный, поэтому правая
часть меньше нуля, и мы пришли к
противоречию.
.
Но в правой части этой цепочки равенств
первый член по предположению отрицательный,
а второй неположительный, поэтому правая
часть меньше нуля, и мы пришли к
противоречию.
Доказательство в
случае
![]() аналогично.
аналогично.
Теорема доказана.
Билет 23
Правило Лопиталя. Случай 0/0.
Теорема 1: (Неопределенность вида 0/0)
Пусть
f(x)
и g(x)
дифференцируемы в некоторой окрестности
точки а,
![]()
![]() в
этой окрестности и
в
этой окрестности и
![]() в
той же окрестности, тогда, если
в
той же окрестности, тогда, если
![]() ,
то
,
то
![]()
Доказательство:
1) a – конечное.
Доопределим функции: f(a)=0 и g(а) = 0; f(x) и g(x) непрерывны на [a;x]
![]()
![]() при
при
![]()
f(a)=g(a)=0 =>
![]()
2)
![]()
Пусть
![]()
![]()
Введем
функции
![]() и
и
![]()
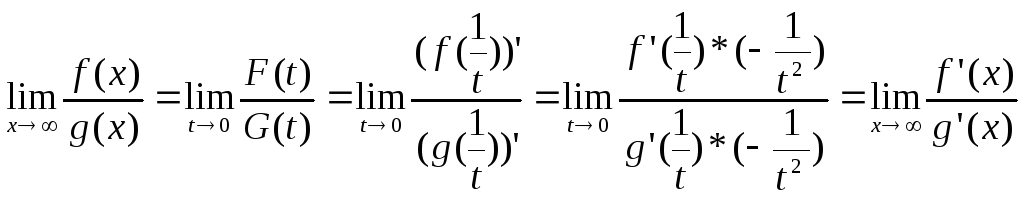
Теорема доказана.
Замечание: обратное неверно.
Пример:
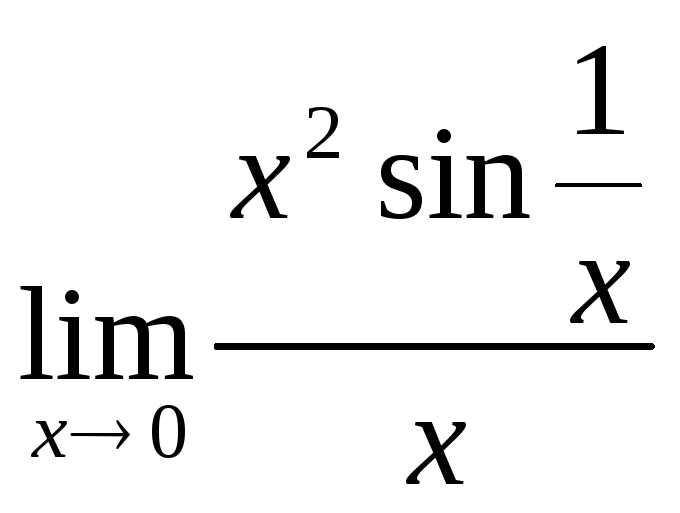
Билет 24
Правило Лопиталя. Случай .
Теорема:
Пусть
функции f
и g
определены и дифференцируемы в некоторой
окрестности точки a
и![]() и
и
![]() в
некоторой выколотой окрестности точки
a,
тогда, если
в
некоторой выколотой окрестности точки
a,
тогда, если
![]() ,
то
,
то
![]() и
и ![]()
Доказательство:
Возьмем
произвольную последовательность
![]() ,
,
![]() ,
,
![]() ,
тогда по определению предела по Гейне
,
тогда по определению предела по Гейне
![]() и
и
![]()
Тогда
![]() - для f(x)
определение предела вида |f(x)|>C,
где C
=
- для f(x)
определение предела вида |f(x)|>C,
где C
=![]()
![]() - аналогично для
g(x)
- аналогично для
g(x)
Тогда можно найти такой номер, для которого будут выполняться оба неравенства:
![]()
![]() ,
, ![]()
Используя
термины
![]() можно записать:
можно записать:
![]() ,
,
![]() Пояснение:
Пояснение:
![]() ,
а т.к.
,
а т.к.
![]()
![]()
Найдем
теперь предел отношения
![]() к
к
![]() :
:
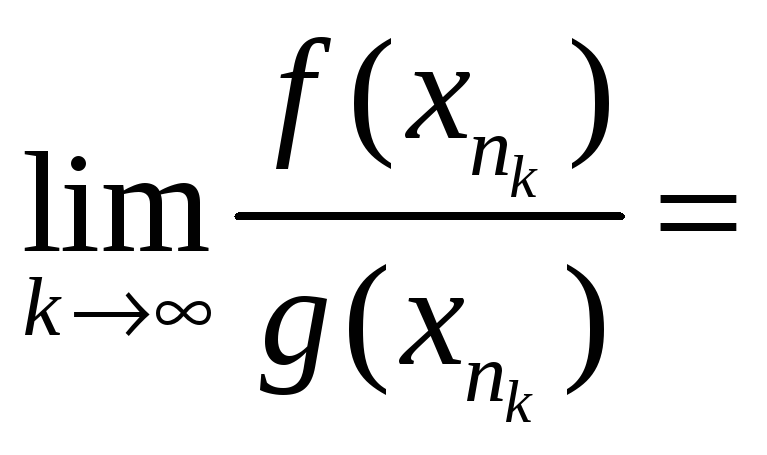 [
можно добавить или отнять
[
можно добавить или отнять
![]() ,
предел от этого не изменится ]
,
предел от этого не изменится ]
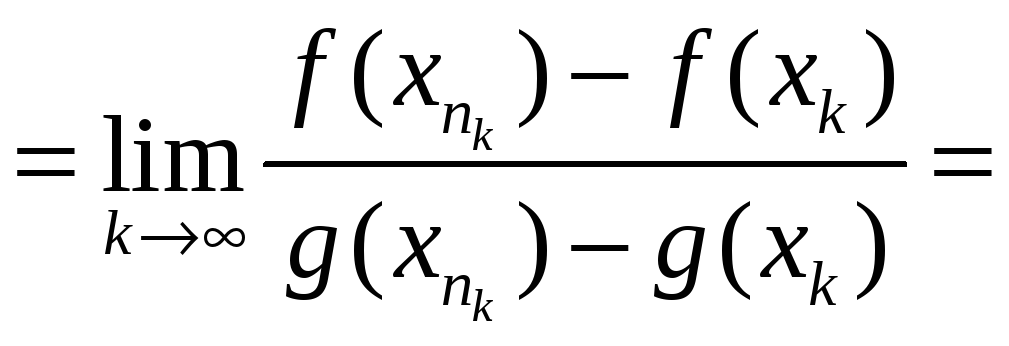 [
воспользуемся теоремой Коши:
[
воспользуемся теоремой Коши:
![]() или
или
![]() - смотря, что больше]
- смотря, что больше]
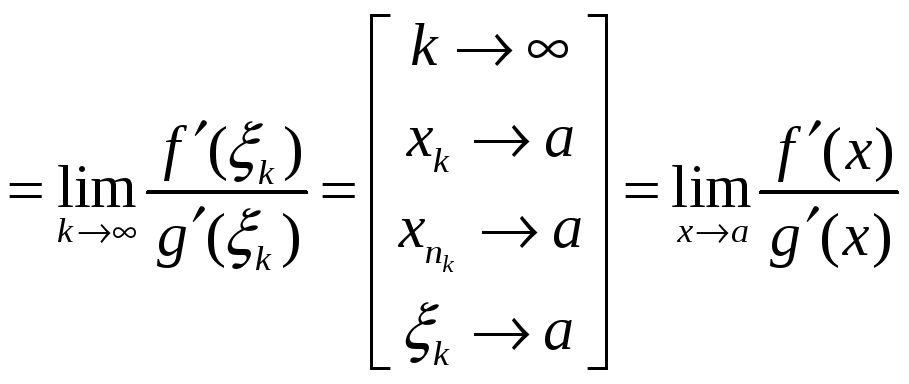 - по определению
предела по Гейне.
- по определению
предела по Гейне.
Мы получили еще
не совсем теорему о сходимости
последовательности через
подпоследовательности, ( ее формулировка:
если
![]() такова, что из любой её подпоследовательности
такова, что из любой её подпоследовательности
![]() можно извлечь в свою очередь
подпоследовательность
можно извлечь в свою очередь
подпоследовательность
![]() ,
сходящуюся к конечному или бесконечному
А, то предел
,
сходящуюся к конечному или бесконечному
А, то предел
![]() =А)
мы пока что только из самой последовательности
выделили сходящуюся подпоследовательность,
а это еще не значит, что сама
последовательность сходится.
=А)
мы пока что только из самой последовательности
выделили сходящуюся подпоследовательность,
а это еще не значит, что сама
последовательность сходится.
Теперь возьмем
произвольную последовательность
![]() и её произвольную подпоследовательность
и её произвольную подпоследовательность
![]() ,
тогда по только что доказанному из
подпоследовательности
,
тогда по только что доказанному из
подпоследовательности
![]() мы можем выделить подпоследовательность
мы можем выделить подпоследовательность
![]() ,
сходящуюся к
,
сходящуюся к
![]() ,
т. е.
,
т. е.
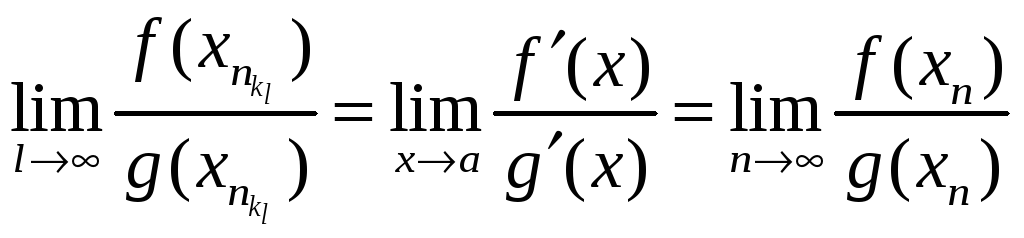
Теперь мы взяли
произвольную последовательность,
поэтому
![]()
Причем важно, чтобы предел отношения производных существовал. Теорема доказана.
Билет 25
