Достаточное условие невозрастания (неубывания) функции на отрезке. Условие постоянства функции на отрезке.
Определение:
Функция
называется строго возрастающей на
отрезке [a,b],
если для любых точек
,
из [a,b],
удовлетворяющих неравенству
,
имеет место неравенство
.
Определение:
Функция
называется неубывающей на [a,b],
если из того, что
и
следует, что
.
Определение:
Функция
называется строго убывающей на отрезке
[a,b],
если из того, что
и
следует, что
.
Определение:
Функция
называется невозрастающей на [a,b],
если из того, что
и
следует, что
.
Пример:
Если
убывает на
и на
,
то нельзя говорить, что
убывает на
.
Теорема
1: (необходимое
условие возрастания (неубывания) функции
в точке
)
Если функция
возрастает (неубывает) в точке
и дифференцируема в
,
то
.
Доказательство:
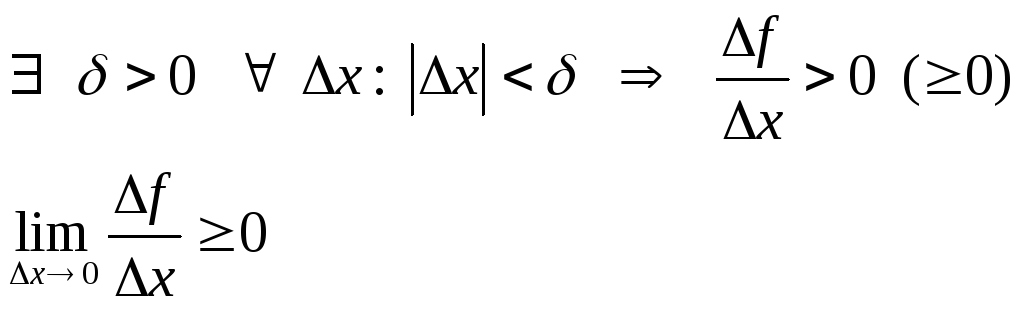
Теорема доказана.
Пример:
возрастает в 0 и
Теорема
1’:
(необходимое условие убывания
(невозрастания) функции в точке
)
Если функция
убывает (невозрастает) в точке
и дифференцируема в
,
то
.
Доказательство – аналогично теореме 1.
Теорема 2: (достаточное условие возрастания)
Если функция
дифференцируема в
и
,
то
возрастает в точке
.
Доказательство:
возрастает.
Теорема доказана.
Замечание:
Если в точке
,
то ни про возрастание, ни про убывание
ничего сказать нельзя.
Билет 16
Достаточные условия экстремума.
Теорема 1: (первое достаточное условие существования экстремума)
Если
f(x)
дифференцируема в
,
f’
имеет разные знаки слева и справа от Xo
=> Xo
– точка экстремума.
Доказательство:
Т.к f(x) с одной стороны возрастает, с другой убывает, т.е.
- max
-
min
Теорема доказана.
Теорема 2: (второе достаточное условие существования экстремума)
Если
в
f(
)=0,
f’’(
)>0
– min;
f’’(
)<0
– max
Доказательство:
f’(
)=0,
существует f’’(
)=>
f’
определена в U(
)
f’(x)
в точке
возрастает(f’’(
)>0)
f’(x)
в точке
убывает(f’’(
)<0)
1)
f’’(
)>0
f’(x)
возрастает, f’(
)=0
=>
п
ри
x<
при
x<
=>
– точка минимума
2)
Аналогично для f’’(
)<0…
Билет 17
Формула Тейлора для многочленов.
Рассмотрим произвольный многочлен степени n:
(1) 
Пусть
a
– любое фиксированное число, тогда,
полагая
,
получим
(2) 
Это
выражение называют разложение многочлена
по степеням
.
Здесь
– числа, зависящие от
и
,
– коэффициенты разложения
по степеням
.
Подставим
в выражение (2)
,
получим
(3) 
Найдем
последовательные производные
и подставим в ним
Таким
образом, многочлен
может быть представлен в виде
или
Последняя
формула называется формулой Тейлора
для многочлена
по степеням
.
Отметим, что правая часть этого выражения
фактически не зависит от
.
Билет 18
Формула Тейлора для дифференцируемых функций.
Если функция f(x)
n
раз дифференцируема в точке а, то для
нее существует многочлен
- это многочлен Тейлора n-го
порядка функции f(x)
в точке a.
Обозначим за
- на сколько многочлен отличается от
самой функции.
называют остаточным членом. Нужно
доказать, что для «хороших» функций
будет достаточно мало. Докажем теорему,
которую сформулируем в конце. =))
Рассмотрим функцию f; зафиксируем точку a, в которой будем раскладывать функцию, и произвольную точку x, такую что f(x) n-1 раз дифференцируема на [a,x] и n раз дифференцируема на (a,x). В точке а функция дифференцируема n-1 раз, значит для нее можно составить многочлен Тейлора n-1 порядка.
Представим
в
виде:
,
где р – произвольное число, H
– некоторая функция, зависящая от x.
Рассмотрим функцию
:
Рассмотрим F(u)
на [a,x]:
F(u)
непрерывная на [a,x],
дифференцируема на (a,x),
F(x)=F(a)
по
теореме Ролля
;
продифференцируем:
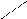
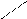
- и почти все
взаимно уничтожается.
,
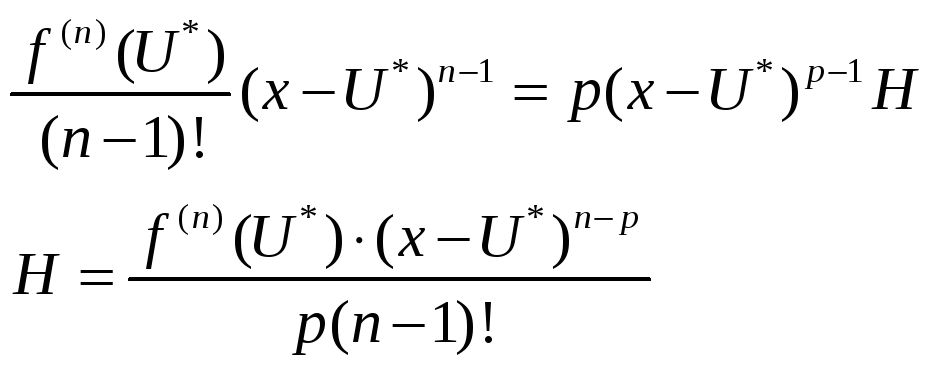
тогда
;
Подставим
теперь p:=n;
-
это остаточный член в форме Лагранжа.
Подставим теперь p:=1
- это остаточный
член в форме Коши.
Рассмотрим форму Лагранжа:
Пусть теперь f имеет непрерывную n-ю производную в точке а. Это означает, что на [a,x) функция n раз дифференцируема. Значит f(x) можно представить в виде:
;
,
т.к. производная непрерывна. Тогда
можно представить в виде:
;
- это формула
Тейлора с остаточным членом в форме
Пеано.
Таким образом, мы доказали следующую теорему:
Теорема
Если функция n-1 раз дифференцируема на [a,x], n раз на (a,x), то она раскладывается по формуле Тейлора с остаточными членами в форме Лагранжа и Коши. Если функция f(x) имеет непрерывную n-ю производную в точке а, то в окрестности точки а она раскладывается по формуле Тейлора с остаточными членами в форме Лагранжа, Коши и Пеано.
Теорема (о единственности разложения функции по формуле Тейлора в форме Пеано)
Если
,
то
,
-
коэффициенты из формулы Тейлора. Т.е.
если есть какие-то другие коэффициенты
,
то они тоже есть коэффициенты из формулы
Тейлора:
Доказательство.
Устремим
,
получим, что
,
т.к.
;
тогда
сократив
на
,
получим:
и опять же
если
.
И так мы можем проделать до n-го коэффициента. Теорема доказана.
Билет 19