
- •Производная. Определение, непрерывность функции, имеющей производную.
- •Геометрический смысл производной.
- •Арифметические свойства производной.
- •Производная обратной функции.
- •Производная сложной функции.
- •Производные элементарных функций.
- •Билет 7 Дифференциал функции. Определение. Геометрический смысл.
- •Необходимое и достаточное условие дифференцируемости.
- •Теорема 1: Для того, чтобы функция была дифференцируемой в точке , необходимо и достаточно , чтобы она имела конечную производную в этой точке.
- •Производные высших порядков. Формула Лейбница.
- •Дифференциалы высших порядков. Инвариантность формы первого дифференциала. Неинвариантность формы дифференциалов второго и высших порядков.
- •Возрастание (убывание) функции в точке. Необходимое и достаточное условие. Теорема Ферма.
- •Теорема Ролля.
- •Теорема Коши. Физический смысл.
- •Теорема о среднем Лагранжа.
- •Достаточное условие невозрастания (неубывания) функции на отрезке. Условие постоянства функции на отрезке.
- •Достаточные условия экстремума.
- •Формула Тейлора для многочленов.
- •Формула Тейлора для дифференцируемых функций.
- •Формула Тейлора для важнейших элементарных функций.
- •Билет 20 Выпуклость функции в точке. Достаточное условие.
- •Теорема 1 (Достаточное условие существования точки перегиба).
- •Непрерывна в и . Тогда, если - нечетное число, то кривая обращена выпуклостью вверх или вниз в зависимости от того, будет ли или, а если четное, то есть точка перегиба кривой.
- •Выпуклость функции на отрезке. Необходимое и достаточное условие.
- •Правило Лопиталя. Случай 0/0.
- •Правило Лопиталя. Случай .
- •Раскрытие неопределенностей вида , ,,, .
- •Асимптота. Уравнение наклонной асимптоты.
- •Первообрáзная. Неопределенный интеграл. Свойства.
- •Замена переменной в неопределенном интеграле.
- •Интегрирование по частям неопределенного интеграла.
- •Интегрирование простейших рациональных дробей
- •Интегрирование рациональных дробей.
- •Интегрирование выражений вида.
- •Первая подстановка Эйлера (Леонарда)
- •Интегрирование тригонометрических выражений.
- •Тригонометрические подстановки.
- •Определенный интеграл Римана. Эквивалентные определения. Условие Коши.
- •Ограниченность интегрируемой функции.
- •Суммы Дарбу. Их Свойства.
- •Суммы Дарбу и интегрируемость функции по Риману.
- •Билет 41 Основная теорема о существовании определенного интеграла Римана.
- •Равномерная непрерывность функции. Модуль непрерывности.
- •Теорема 2 Функция непрерывная на отрезке, равномерно непрерывна на нем ().
- •Интегрируемость по Риману непрерывной функции.
- •Интегрируемость по Риману монотонной функции.
- •Аддитивное и однородные свойства определенного интеграла Римана.
- •Неравенства для определенного интеграла Римана и теорема о среднем.
- •Интеграл как функция верхнего предела. Непрерывность и дифференцируемость. Теорема Ньютона-Лейбница.
- •Билет 48 Определение площади. Площадь криволинейной трапеции. Площадь в полярных координатах.
- •Определение объёма. Объем тела вращения.
- •Длина дуги кривой. Определение и вычисление.
Неравенства для определенного интеграла Римана и теорема о среднем.
Теорема 1:
Если
функции
![]() интегрируемы на
интегрируемы на
![]() и
и
![]()
![]()
Доказательство:
![]() выполняется
неравенство
выполняется
неравенство
![]() ,
тогда
,
тогда
![]() .
Так как интегралы по условию существуют,
по теореме о предельном переходе под
знаком неравенства,
.
Так как интегралы по условию существуют,
по теореме о предельном переходе под
знаком неравенства,
![]() .
Теорема доказана.
.
Теорема доказана.
Следствие:
Если
![]() -
интегрируема на
-
интегрируема на
![]() ,
то, по доказанному выше,
,
то, по доказанному выше,
![]() - интегрируем на данном отрезке; тогда
- интегрируем на данном отрезке; тогда
![]()
Доказательство:
Известно
неравенство:
![]() ; по данной теореме
; по данной теореме
![]() ;
из самого правого интеграла минус можно
вынести; получим:
;
из самого правого интеграла минус можно
вынести; получим:
![]() .
Следствие доказано.
.
Следствие доказано.
Теорема 2: (о среднем)
Пусть
![]() интегрируемы
на
интегрируемы
на
![]() ,
причем
,
причем
![]() на данном промежутке, тогда
на данном промежутке, тогда
![]() ,
где
,
где
![]() ,
,
![]()
и
![]()
Замечание: sup и inf существуют, т.к. функция на данном промежутке интегрируема, а значит ограничена.
Доказательство:
Запишем
неравенство:
![]() и домножим его на
и домножим его на
![]() :
:
![]() ;
тогда по теореме о неравенствах это
неравенство сохранится и в интегралах:
;
тогда по теореме о неравенствах это
неравенство сохранится и в интегралах:
![]() (
(![]() )
)
Если
![]() ,
то и интеграл
,
то и интеграл
![]() и неравенство (
и неравенство (![]() )
выполняется.
)
выполняется.
Если
![]() ,
тогда по теореме о неравенствах
,
тогда по теореме о неравенствах
![]() ,
значит можно неравенство (
,
значит можно неравенство (![]() )
на него разделить:
)
на него разделить:
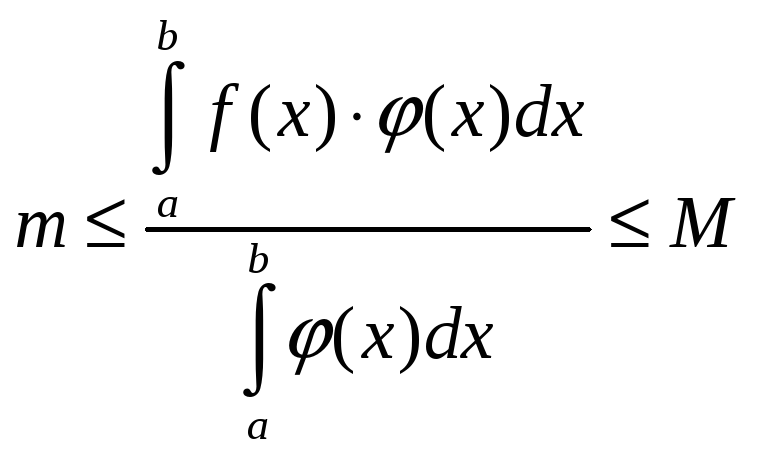 и принимаем за
и принимаем за
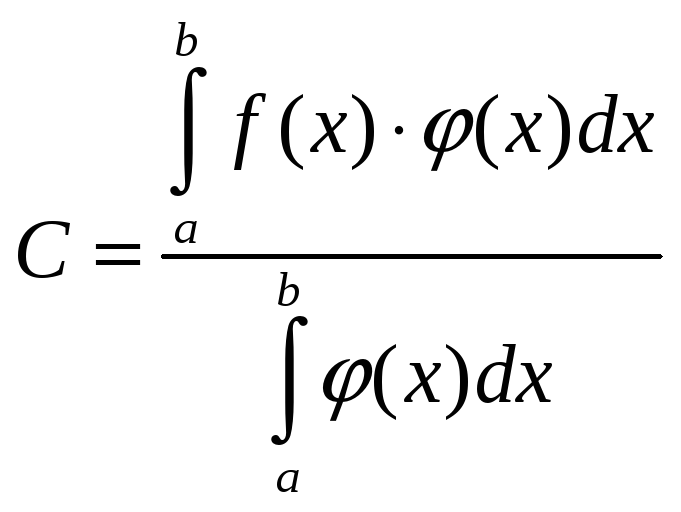 .
Теорема доказана.
.
Теорема доказана.
Следствие:
Если
![]() непрерывна
на
непрерывна
на
![]() и выполняется условие теоремы, то
и выполняется условие теоремы, то
![]()
Доказательство:
Т.к.
![]() непрерывна
на
непрерывна
на
![]() ,
то она достигает своего max
и min
значения, а в силу непрерывности sup=max,
inf=min;
значит
,
то она достигает своего max
и min
значения, а в силу непрерывности sup=max,
inf=min;
значит
![]() - по теореме о промежуточных значениях
непрерывной функции. Следствие доказано.
- по теореме о промежуточных значениях
непрерывной функции. Следствие доказано.
Следствие к следствию:
Если
![]() непрерывна
на
непрерывна
на
![]() ,
то
,
то
![]()
Доказательство:
Возьмем
![]() ,
тогда
,
тогда
![]() (по
следствию)
(по
следствию)
![]() .
Следствие доказано.
.
Следствие доказано.
Г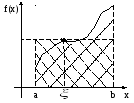 еометрический
смысл этого следствия:
еометрический
смысл этого следствия:
Если считать
площадь криволинейной трапеции, то
найдется такая точка
![]() ,
что площадь этой криволинейной трапеции
будет равна площади прямоугольника с
высотой
,
что площадь этой криволинейной трапеции
будет равна площади прямоугольника с
высотой
![]() .
.
Билет 47
Интеграл как функция верхнего предела. Непрерывность и дифференцируемость. Теорема Ньютона-Лейбница.
Рассмотрим функцию
![]() ,
интегрируемую на отрезке
,
интегрируемую на отрезке
![]() .
По аддитивному свойству интеграла:
.
По аддитивному свойству интеграла:
![]() ,
можно найти отрезок
,
можно найти отрезок
![]() на котором представляется возможным
рассмотреть функцию
на котором представляется возможным
рассмотреть функцию
![]() .
.
Теорема:
Если функция
![]() интегрируема на отрезке
интегрируема на отрезке
![]() ,
то
,
то
![]() непрерывна на отрезке
непрерывна на отрезке
![]() .
.
Доказательство:
Рассмотрим функцию
![]() ,
,
![]() ,
где
,
где
![]() ,
,
![]() ,
,
![]() ,
где
,
где
![]()
Теорема доказана.
Теорема:
Пусть функция
![]() интегрируема на отрезке
интегрируема на отрезке
![]() ,
непрерывна в точке
,
непрерывна в точке
![]() ,
тогда функция
,
тогда функция
![]() дифференцируема в точке
дифференцируема в точке
![]() и
и
![]() .
.
Доказательство:
![]() ,
,
![]() ,
,
![]()
![]()
![]() ,
т.е.
,
т.е.
![]() .
.
Теорема доказана.
Следствие:
Если функция
![]() непрерывна на отрезке
непрерывна на отрезке
![]() ,
то
,
то
![]() ,
т.е.
,
т.е.
![]() - первообразная
- первообразная
![]() .
.
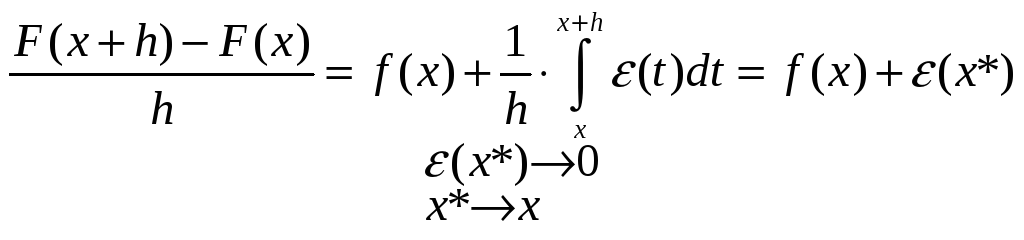 ,
,
Функция
![]() непрерывна в точке
непрерывна в точке
![]() ,
,
![]() ;
;
![]() ,
где
,
где
![]() непрерывна на отрезке
непрерывна на отрезке
![]() .
Заключаем, что
.
Заключаем, что
![]() .
.
Т.е. любая непрерывная функция имеет первообразную.
Теорема доказана.
Формула Ньютона-Лейбница:
Функция
![]() непрерывна на отрезке
непрерывна на отрезке
![]() ,
тогда она имеет первообразную. Пусть
,
тогда она имеет первообразную. Пусть
![]() - её произвольная первообразная. Тогда
- её произвольная первообразная. Тогда
![]() .
.
Доказательство:
Функция
![]() непрерывна на отрезке
непрерывна на отрезке
![]() ,
,
![]() - первообразная функции
- первообразная функции
![]() ,
,
![]() ,
,
![]() ,
,
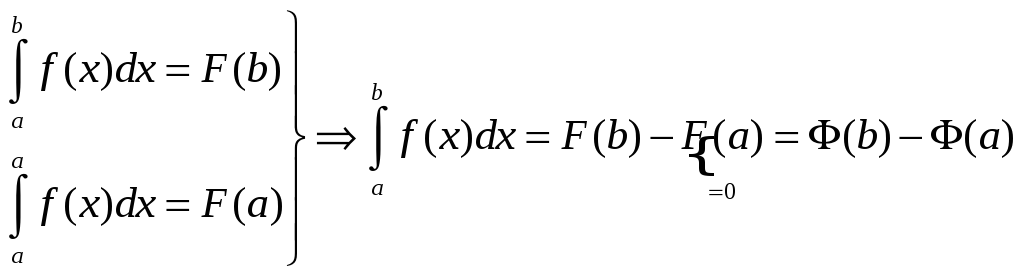 . Теорема
доказана.
. Теорема
доказана.
Билет 48 Определение площади. Площадь криволинейной трапеции. Площадь в полярных координатах.
Определение:
Пусть множество
![]() и A
– ограничено. Рассмотрим множество
и A
– ограничено. Рассмотрим множество
![]() (объединение прямоугольников), такое
что
(объединение прямоугольников), такое
что
![]() ,
и множество
,
и множество
![]() ,
такое что
,
такое что
![]() ,
и назовем
,
и назовем
![]() и
и
![]() фигурами. Площади этих фигур
фигурами. Площади этих фигур
![]() и
и
![]() можно
посчитать. Т.к. множество
можно
посчитать. Т.к. множество
![]() оганичено
сверху (S(A))
оганичено
сверху (S(A))![]() .
Аналогично
.
Аналогично
![]() ограничено снизу (нулем)
ограничено снизу (нулем)
![]() .
Если
.
Если
![]() ,
то это площадь A,
а множество называется квадрируемым.
,
то это площадь A,
а множество называется квадрируемым.
П ример1:
Пусть τ – отрезок и
ример1:
Пусть τ – отрезок и
![]() .
.
![]() Ø.
При этом S(M΄)=0
и
Ø.
При этом S(M΄)=0
и
![]() .
Пусть длина отрезка равна d,
тогда
.
Пусть длина отрезка равна d,
тогда
![]() ,
а
,
а
![]() длины d
и высоты h.
Тогда
длины d
и высоты h.
Тогда
![]() .
Получили S(τ)=0.
.
Получили S(τ)=0.
П ример2:
ример2:
 .
.
![]() ,
,
![]() Ø
и
Ø
и
![]() ,
т.к. никакой прямоугольник полностью
не лежит в этом множестве.
,
т.к. никакой прямоугольник полностью
не лежит в этом множестве.
![]() ,
т.е.
,
т.е.
![]() ,
поэтому
,
поэтому
![]() .
Получаем, что
.
Получаем, что
![]() ,
поэтому множество A
- не квадрируемое.
,
поэтому множество A
- не квадрируемое.
Пусть f(x)≥0 на [a,b]. Криволинейная трапеция T - множество (x,y), такое что a≤x≤b и 0≤y≤f(x).
Теорема: (О площади криволинейной трапеции).
Пусть
функция f(x)≥0
на [a,b].
Криволинейная трапеция T
квадрируема тогда и только тогда(),
когда функция f(x)
интегрируема на [a,b].
При этом площадь T
равна:
![]() .
.
Д
 оказательство:
:
По основной теореме
оказательство:
:
По основной теореме
![]() .
Найдутся такие
.
Найдутся такие
![]() и
и
![]() ,
что
,
что
![]() и
и
![]() .
Тогда
.
Тогда
![]() .
.
:
![]() ,
так как криволинейная трапеция T
квадрируема. Тогда
,
так как криволинейная трапеция T
квадрируема. Тогда
![]()
![]() Обе интегральные суммы стремятся к
одному и тому же числу (S).
Обе интегральные суммы стремятся к
одному и тому же числу (S).
![]() ,
,
![]() .
Следовательно
.
Следовательно
![]() ,
поэтому функция f(x)
интегрируема (из следствия основной
теоремы).
,
поэтому функция f(x)
интегрируема (из следствия основной
теоремы).
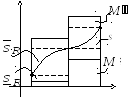
Пример.
x2+y2=R2.
a≤x≤b
(a=-R,
b=R),
и 0≤y≤![]() .
При этом
.
При этом
Замечание
к определению площади:
Множества
![]() можно заменить на любые другие квадрируемые
множества. Если
можно заменить на любые другие квадрируемые
множества. Если
![]() - фигуры,
- фигуры,
![]() - квадрируемые множества, т.е. существуют
площади
- квадрируемые множества, т.е. существуют
площади
![]() и при этом
и при этом
![]() ,
то при
,
то при
![]() получим все то же самое.
получим все то же самое.
П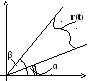
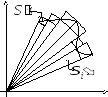 усть
множество задано в полярных
координатах:
x=r·cost,
y=r·sint.
Рассмотрим множество A,
такое, что α≤t≤β
и 0≤r≤r(t).
Введем разбиение угла [α,β]:
α=t0<t1<t2<…<tn=β.
При этом Δti=[ti
,ti+1].
Рассмотрим сектора окружностей ri=mi
– это будут сектора
усть
множество задано в полярных
координатах:
x=r·cost,
y=r·sint.
Рассмотрим множество A,
такое, что α≤t≤β
и 0≤r≤r(t).
Введем разбиение угла [α,β]:
α=t0<t1<t2<…<tn=β.
При этом Δti=[ti
,ti+1].
Рассмотрим сектора окружностей ri=mi
– это будут сектора
![]() и ri=Mi
– это будут сектора
и ri=Mi
– это будут сектора
![]() .
.
![]() и
и
![]() .
Окружности (с углом 2π) соответствует
площадь πR2,
а сектору с углом α – площадь αR2/2.
Поэтому
.
Окружности (с углом 2π) соответствует
площадь πR2,
а сектору с углом α – площадь αR2/2.
Поэтому
![]() и
и
![]() .
.
![]() и
и
![]() -
нижняя и верхняя суммы Дарбý для функции
f=r2/2.
Получим
-
нижняя и верхняя суммы Дарбý для функции
f=r2/2.
Получим
![]() и
и
![]() .
То есть площадь S(A)
существует и равна S
(т.е. A
квадрируема) тогда и только тогда, когда
существует интеграл
.
То есть площадь S(A)
существует и равна S
(т.е. A
квадрируема) тогда и только тогда, когда
существует интеграл
![]()
Билет 49
