
- •Производная. Определение, непрерывность функции, имеющей производную.
- •Геометрический смысл производной.
- •Арифметические свойства производной.
- •Производная обратной функции.
- •Производная сложной функции.
- •Производные элементарных функций.
- •Билет 7 Дифференциал функции. Определение. Геометрический смысл.
- •Необходимое и достаточное условие дифференцируемости.
- •Теорема 1: Для того, чтобы функция была дифференцируемой в точке , необходимо и достаточно , чтобы она имела конечную производную в этой точке.
- •Производные высших порядков. Формула Лейбница.
- •Дифференциалы высших порядков. Инвариантность формы первого дифференциала. Неинвариантность формы дифференциалов второго и высших порядков.
- •Возрастание (убывание) функции в точке. Необходимое и достаточное условие. Теорема Ферма.
- •Теорема Ролля.
- •Теорема Коши. Физический смысл.
- •Теорема о среднем Лагранжа.
- •Достаточное условие невозрастания (неубывания) функции на отрезке. Условие постоянства функции на отрезке.
- •Достаточные условия экстремума.
- •Формула Тейлора для многочленов.
- •Формула Тейлора для дифференцируемых функций.
- •Формула Тейлора для важнейших элементарных функций.
- •Билет 20 Выпуклость функции в точке. Достаточное условие.
- •Теорема 1 (Достаточное условие существования точки перегиба).
- •Непрерывна в и . Тогда, если - нечетное число, то кривая обращена выпуклостью вверх или вниз в зависимости от того, будет ли или, а если четное, то есть точка перегиба кривой.
- •Выпуклость функции на отрезке. Необходимое и достаточное условие.
- •Правило Лопиталя. Случай 0/0.
- •Правило Лопиталя. Случай .
- •Раскрытие неопределенностей вида , ,,, .
- •Асимптота. Уравнение наклонной асимптоты.
- •Первообрáзная. Неопределенный интеграл. Свойства.
- •Замена переменной в неопределенном интеграле.
- •Интегрирование по частям неопределенного интеграла.
- •Интегрирование простейших рациональных дробей
- •Интегрирование рациональных дробей.
- •Интегрирование выражений вида.
- •Первая подстановка Эйлера (Леонарда)
- •Интегрирование тригонометрических выражений.
- •Тригонометрические подстановки.
- •Определенный интеграл Римана. Эквивалентные определения. Условие Коши.
- •Ограниченность интегрируемой функции.
- •Суммы Дарбу. Их Свойства.
- •Суммы Дарбу и интегрируемость функции по Риману.
- •Билет 41 Основная теорема о существовании определенного интеграла Римана.
- •Равномерная непрерывность функции. Модуль непрерывности.
- •Теорема 2 Функция непрерывная на отрезке, равномерно непрерывна на нем ().
- •Интегрируемость по Риману непрерывной функции.
- •Интегрируемость по Риману монотонной функции.
- •Аддитивное и однородные свойства определенного интеграла Римана.
- •Неравенства для определенного интеграла Римана и теорема о среднем.
- •Интеграл как функция верхнего предела. Непрерывность и дифференцируемость. Теорема Ньютона-Лейбница.
- •Билет 48 Определение площади. Площадь криволинейной трапеции. Площадь в полярных координатах.
- •Определение объёма. Объем тела вращения.
- •Длина дуги кривой. Определение и вычисление.
Суммы Дарбу. Их Свойства.
Определение:
Пусть
![]() ограничена
на отрезке
ограничена
на отрезке
![]() .
Введём разбиение R
этого отрезка.
.
Введём разбиение R
этого отрезка.
R:
![]() ,
,
![]() .
.
Тогда можем составить выражения:
![]() - нижняя сумма
Дарбу,
- нижняя сумма
Дарбу,
![]() - верхняя сумма Дарбу.
- верхняя сумма Дарбу.
![]() ,
,
![]() .
.
Пусть
![]() ограничена
на отрезке
ограничена
на отрезке
![]() .
Введём разбиение R
этого отрезка.
.
Введём разбиение R
этого отрезка.
R:
![]() ,
,
![]() .
.
Тогда можем составить выражения:
![]() - нижняя сумма
Дарбу,
- нижняя сумма
Дарбу,
![]() - верхняя сумма Дарбу.
- верхняя сумма Дарбу.
![]() ,
,
![]() .
.
Свойства сумм Дарбу:
1)
![]() ,
для одного и того же разбиения.
,
для одного и того же разбиения.
2) Рассмотрим два
разбиения в случае, когда одно разбиение
является продолжением другого. Т.е.
![]() -
продолжение
-
продолжение
![]() ,
если все точки
,
если все точки
![]() являются точками
являются точками
![]() .
.
![]()
Д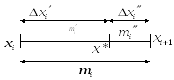 обавление
точек не увеличивает
обавление
точек не увеличивает
![]() и не уменьшает
и не уменьшает
![]() .
Пусть
.
Пусть
![]() получается из
получается из
![]() добавлением одной точки.
добавлением одной точки.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
Заметим, что если
![]() ,
то
,
то
![]() и
и
![]() .
Отсюда заключаем:
.
Отсюда заключаем:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
3)
![]()
![]() ,
,
![]() ,
,
![]() ,
,
=>
![]() ,
т.е.
,
т.е.
![]()
![]() .
.
![]()
![]() - нижний интеграл
(нижняя точная сумма Дарбу).
- нижний интеграл
(нижняя точная сумма Дарбу).
![]()
![]() .
.
![]()
![]() - верхний интеграл
(верхняя точная сумма Дарбу).
- верхний интеграл
(верхняя точная сумма Дарбу).
![]()
![]() .
.
![]() .
.
Билет 40
Суммы Дарбу и интегрируемость функции по Риману.
Теорема:
Функция
![]() интегрируема на отрезке
интегрируема на отрезке
![]() тогда и только тогда, когда
тогда и только тогда, когда
![]() .
.
Доказательство:
Докажем необходимость условия:
Функция
![]() интегрируема на отрезке
интегрируема на отрезке
![]() .
.
Пусть
![]() ,
тогда
,
тогда
![]()
![]()
![]() ,
т.е.
,
т.е.
![]() .
.
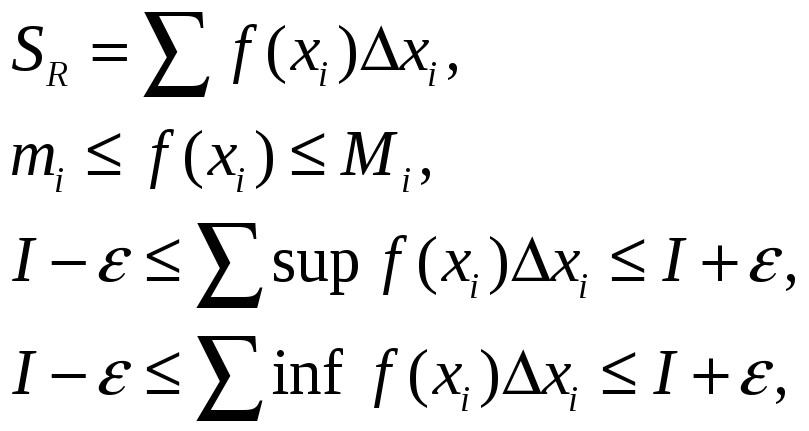
т.е.
![]() и
и
![]() .
.
Далее
имеем:
![]() ,
т.е.
,
т.е.
![]() .
.
Необходимость доказана.
Докажем достаточность условия:
![]() .
.
![]()
![]()
![]() .
.
![]() .
.
Докажем,
что
![]() .
.
![]()
![]() ,
,
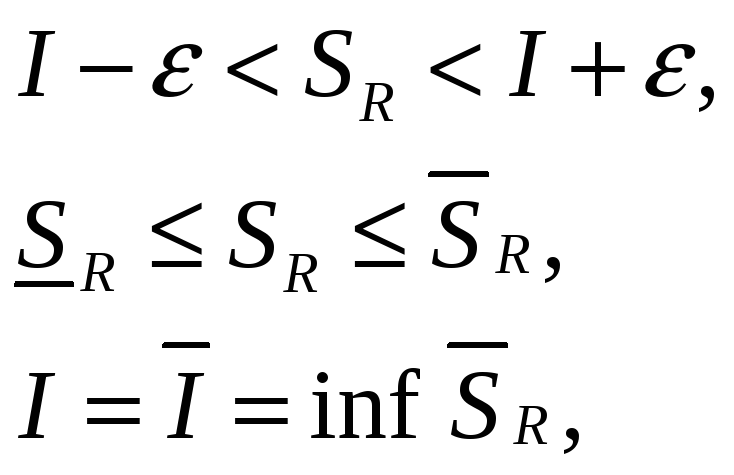
![]()
![]() ,
,
![]() ,
тогда
,
тогда
![]()
![]() ,
т.е.
,
т.е.
![]() ,
,
![]() .
.
Достаточность доказана.
Билет 41 Основная теорема о существовании определенного интеграла Римана.
Теорема (Основная)
Ограниченная
функция f
интегрируема на отрезке [a,b]
тогда и только тогда, когда
![]() .
.
Доказательство:
П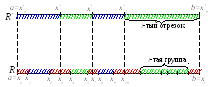 о
теореме об интегрируемости (f интегрируема
о
теореме об интегрируемости (f интегрируема
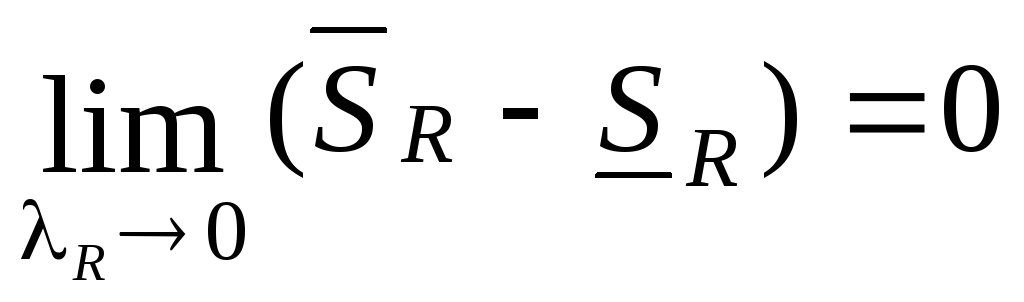 )
функция интегрируема тогда и только
тогда, когда
)
функция интегрируема тогда и только
тогда, когда
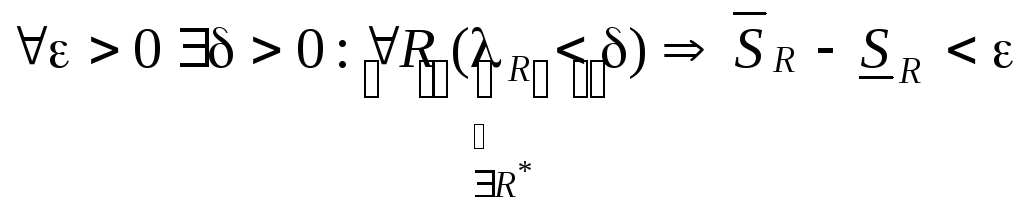 (1). Надо доказать, что если
(1). Надо доказать, что если
![]() .
Т.е. если найдется одно R*,
удовлетворяющее неравенству (1), то оно
(неравенство) будет выполняться для
всех R.
Возьмем произвольное
.
Т.е. если найдется одно R*,
удовлетворяющее неравенству (1), то оно
(неравенство) будет выполняться для
всех R.
Возьмем произвольное
![]() .
Нужно найти δ,
такое чтобы выполнялось неравенство
.
Нужно найти δ,
такое чтобы выполнялось неравенство
![]() .
По условию теоремы
.
По условию теоремы
![]() .
Рассмотрим наше разбиение R*
и произвольное R,
как показано на рисунке. Составим
разность верхней и нижней сумм Дарбý
для нового разбиения R:
.
Рассмотрим наше разбиение R*
и произвольное R,
как показано на рисунке. Составим
разность верхней и нижней сумм Дарбý
для нового разбиения R:
![]() .
Нужно сделать его меньше
.
Нужно сделать его меньше
![]() .
Из условия имеем
.
Из условия имеем
![]() .
Обозначим через Σ первую сумму и разобъем
ее: Σ=Σ1+Σ2.
Σ1 –
такие слагаемые, что элемент нового
разбиения R
содержит в себе хотя бы одну точку
границы старого раазбиения R*.
Все остальное войдет в Σ2.
Рассмотрим отдельно Σ1
и Σ2:
.
Обозначим через Σ первую сумму и разобъем
ее: Σ=Σ1+Σ2.
Σ1 –
такие слагаемые, что элемент нового
разбиения R
содержит в себе хотя бы одну точку
границы старого раазбиения R*.
Все остальное войдет в Σ2.
Рассмотрим отдельно Σ1
и Σ2:
Σ1:
![]() т.к. функция f
– ограничена (k
- константа). Тогда
т.к. функция f
– ограничена (k
- константа). Тогда
![]() (M
и m
– максимум и минимум на [a,b]).
Получим Σ1
(M
и m
– максимум и минимум на [a,b]).
Получим Σ1![]() ,
где λR<δ,
а количество красных отрезков не
превосходит 2n.
Для того чтобы это неравенство выполнялось,
достаточно взять δ<
,
где λR<δ,
а количество красных отрезков не
превосходит 2n.
Для того чтобы это неравенство выполнялось,
достаточно взять δ<![]() /8kn.
Т.е. при δ<
/8kn.
Т.е. при δ<![]() /8kn
Σ1<
/8kn
Σ1<![]() /2.
/2.
Σ2:
разобъем Σ2
на повторные суммы, т.е. Σ2=Σ(Σi).
Σi≤![]() ≤
≤![]() (Mi*-mi*)ΣΔxi*,
где Mj
и mj
– максимум и минимум на j-том
участке. Σi
– группировка тех новых j-тых
участков, которые попали в один и тот
же старый. Получим Σ2
(Mi*-mi*)ΣΔxi*,
где Mj
и mj
– максимум и минимум на j-том
участке. Σi
– группировка тех новых j-тых
участков, которые попали в один и тот
же старый. Получим Σ2![]() Σ1+Σ2<ε,
т.е. Σ<
Σ1+Σ2<ε,
т.е. Σ<![]() .
В итоге:
.
В итоге:
![]() .
Теорема доказана.
.
Теорема доказана.
Следствие
1:
Функция f
– интегрируема на [a,b],
если
![]() с
с
![]() :
:
![]() (если существует такая последовательность
разбиений с мелкостью, стремящейся к
нулю, что модуль разности последовательности
интегральных сумм и интеграла стремится
к нулю).
(если существует такая последовательность
разбиений с мелкостью, стремящейся к
нулю, что модуль разности последовательности
интегральных сумм и интеграла стремится
к нулю).
Следствие
2:
Функция f
– интегрируема на [a,b],
если
![]() (если
верхний интеграл равен нижнему).
(если
верхний интеграл равен нижнему).
Билет 42
