- •Раздел 1. Теория пределов.
- •Раздел 2. Дифференциальное исчисление.
- •Раздел 3. Интегральное исчисление.
- •Раздел 1. Теория пределов
- •§1.1. Предел и непрерывность функции
- •Вычисление пределов
- •§ 1.2. Вычисление пределов
- •Раздел 2. Дифференциальное исчисление
- •§ 2.1. Производная
- •§ 2.2. Правила и формулы вычисления производных
- •§ 2.3. Геометрический и механический смысл производной
- •§ 2.4. Производные высших порядков
- •§2.5. Дифференциал
- •§ 2.6. Правило лопиталя
- •§ 2.7. Исследование функций и построение графиков
- •Раздел 3. Интегральное исчисление
- •§ 3.1. Первообразная
- •§ 3.2. Неопределенный интеграл и его свойства
- •§ 3.3. Основные табличные интегралы
- •§ 3.4. Основные методы интегрирования:
- •§3.5. Определенный интеграл и
- •§ 3.6. Основные свойства и вычисление
§ 3.6. Основные свойства и вычисление
ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
1. Простейшие свойства определенного интеграла
2. Подстановка в определенном интеграле
3. Вычисление определенных интегралов
1. Простейшие свойства определенного интеграла
Рассмотрим основные свойства определенного интеграла. При этом будем предполагать, что функция f(x) непрерывна на отрезке [a, b].
1. При перестановке пределов интегрирования знак интеграла меняется на противоположный:
 (1)
(1)
Д о к а з а т е л ь с т в о.
Пусть
f
(x)
= F'(x)
и, значит,
![]() Тогда
Тогда
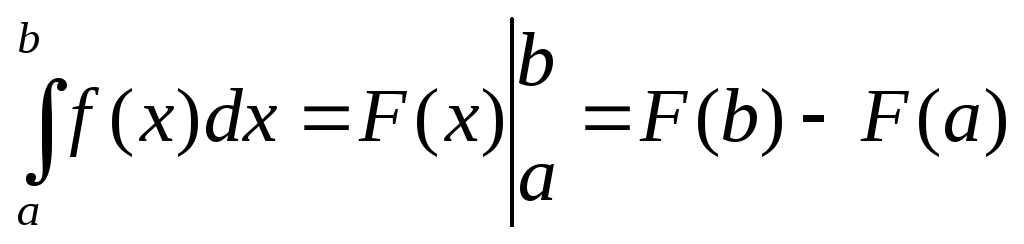 (2).
(2).
 (3).
(3).
Правые части равенств (2) и (3) равны; следовательно, должны быть равны и левые части, т. е. справедливо соотношение (1).
Это свойство позволяет рассматривать интегралы, в которых верхний предел меньше нижнего.
|
Найти
Решение.
|
2. Постоянный
множитель можно вынести за знак
определенного интеграла, т.
е.
 где k
—
постоянная
величина.
где k
—
постоянная
величина.
3. Определенный интеграл от алгебраической суммы функций равен алгебраической сумме определенных интегралов от этих функций, т. е.

4.
Если
а, b,
с принадлежат интервалу, на котором
функция f
(х) непрерывна, то

Д о к а з а т е л ь с т в о. Пусть F (x) – первообразная функции для f(x) . Тогда

2. Подстановка в определенном интеграле
Для вычисления определенного интеграла с помощью подстановки поступают так же, как и при вычислении неопределенного интеграла этим способом. Однако в случае определенного интеграла имеется одна особенность, на которую следует обратить внимание.
Как мы отмечали, метод подстановки заключается в том, что для приведения заданного неопределенного интеграла к табличному выражают аргумент через новую переменную, а затем находят неопределенный интеграл и полученный результат снова выражают через первоначальную переменную. В случае же определенного интеграла нет необходимости возвращаться к первоначальной переменной, однако нужно помнить, что, заменяя переменную под знаком интеграла, следует изменить и пределы интегрирования.
|
Найти
Решение. Воспользуемся
подстановкой u
= 1 – cosx,
откуда du
= sinxdx.
Затем найдем новые пределы интегрирования;
подставляя в равенство u
= 1 – cosx
значения
|
3. Вычисление определенных интегралов
Вычислить определенные интегралы, используя определение, их свойства и метод подстановки.
1)
![]()
Решение.
![]()
2)
![]()
Решение.
![]()
3)
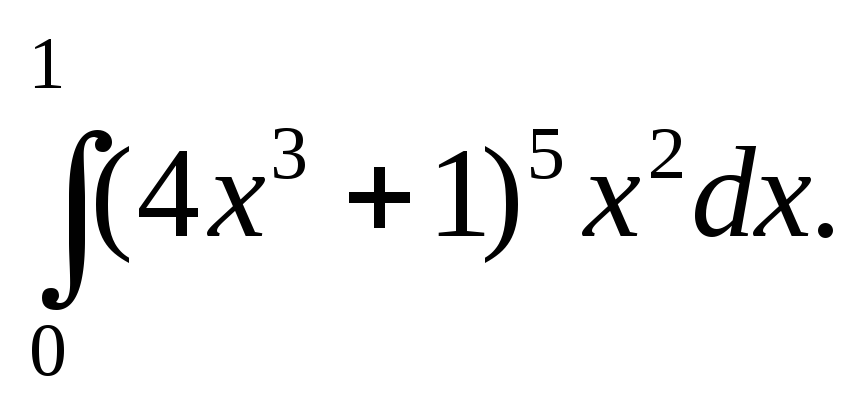
Решение.
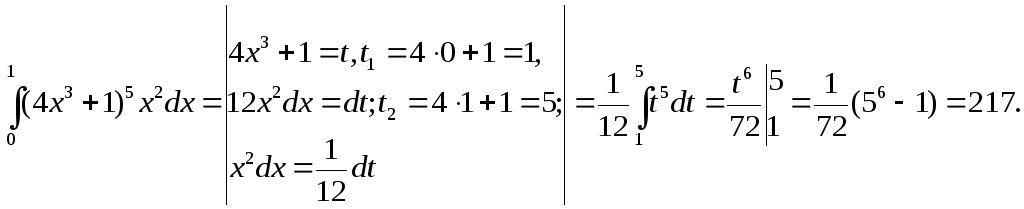
Контрольная работа №3.
Вычислите:
Вариант 1.
1)
![]() 2)
2)
![]()
3)
![]() 4)
4)
![]() 5)
5)
![]()
Вариант 2.
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
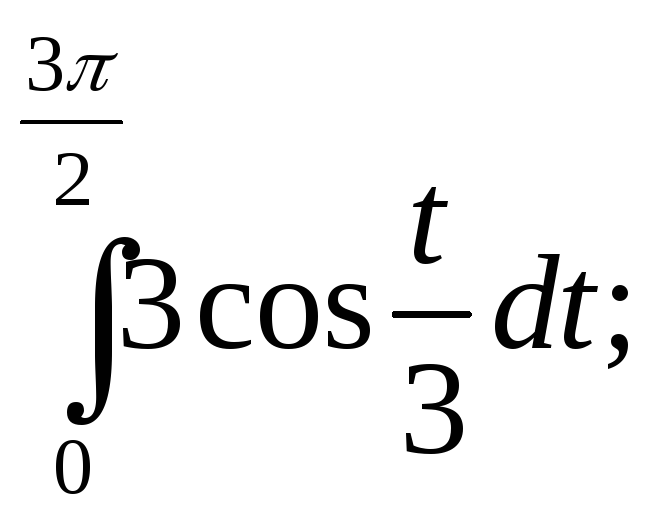 5)
5)
![]()
Вариант 3.
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]()
Вариант 4.
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
 5)
5)
![]()
Вариант 5.
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]()
Вариант 6.
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)

Вариант 7.
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]()
Вариант 8.
1)
![]() 2)
2)
![]()
3)
![]() 4)
4)
![]() 5)
5)
![]()
Вариант 9.
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
 5)
5)

Вариант 10.
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
 5)
5)
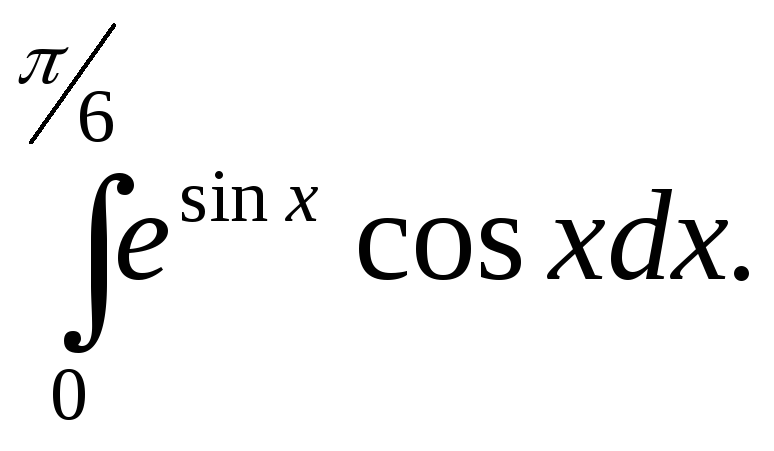
Вопросы для повторения:
-
Что является основной задачей интегрального исчисления?
-
Какая функция называется первообразной для заданной функции?
-
Если F(x) — первообразная для f(x), то каким равенством связаны они между собой?
-
Первообразная определяется неоднозначно. Как это нужно понимать?
-
Почему при интегрировании функций появляется произвольная постоянная?
-
Как записать всю совокупность первообразных функций?
-
Что называется неопределенным интегралом?
-
Чем отличается неопределенный интеграл от первообразной функции?
-
Почему интеграл называется неопределенным?
-
Чему равны производная и дифференциал неопределенного интеграла?
11. В чем заключается правило интегрирования выражения, содержащего постоянный множитель?
-
В чем заключается правило интегрирования алгебраической суммы функций?
-
Чему равен интеграл от дифференциала некоторой функции?
-
Напишите основные формулы интегрирования.
-
Как доказать справедливость каждой формулы интегрирования?
-
Как проверить результат интегрирования?
-
В чем состоит геометрический смысл неопределенного интеграла?
-
Что такое интегральные кривые? Как они расположены друг относительно друга? Могут ли они пересекаться?
-
Что такое определенный интеграл?
20. Сформулируйте основные свойства определенного интеграла.
-
В чем заключается геометрический смысл определенного интеграла?
Литература:
-
Кремер Н.Ш., Путко Б.А., Тришин И.М., Фридман М.Н. Высшая математика для экономистов: Учебник для ВУЗов / Под ред. Кремера Н.Ш. – М.: ЮНИТИ, 2004
-
Филимонова Е.В., Тер-Симонян Н.А. Математика и информатика: Учебное пособие. – М.: ИКТЦ "Маркетинг", 2002.