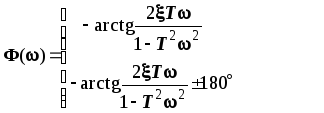курсовая работа / tau-zibben-auf / r-TAU-kursovik-var-83-second-version / MYTAU1
.DOC
Вариант № 83
Структурная схема разомкнутой системы
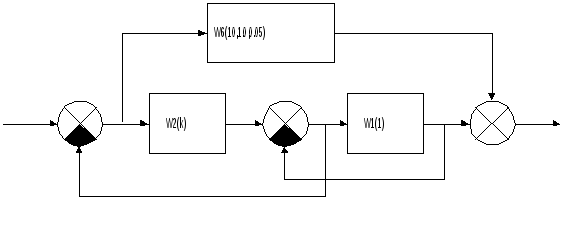
Пункт №1
Получить
передаточную функцию
для разомкнутой системы
Аналитический метод
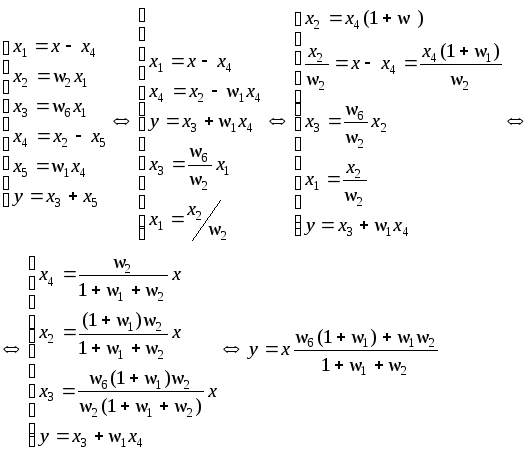
После подстановки получаем передаточную функцию разомкнутой системы
Пункт №2
Построить частотные характеристики типовых звеньев.
Звено №1
-
АФЧХ A(j)
ЛАЧХ L(w)
-
ЛФЧХ Ф(w)
Звено №2
-
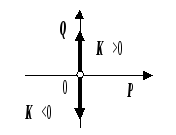
АФЧХ A(j)
ЛАЧХ L(w)
-
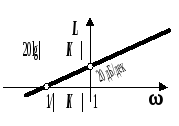
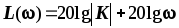
ЛФЧХ Ф(w)
Звено №6
-
АФЧХ A(j)
ЛАЧХ L(w)
|
|
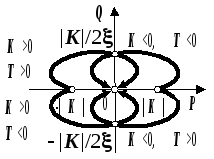
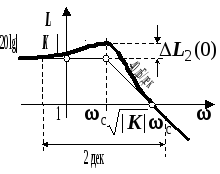
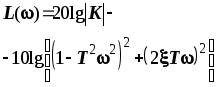
ЛФЧХ Ф(w) |
|---|---|
|
|
|
Пункт №3
Исследовать устойчивость разомкнутой системы от буквенного параметра методами Гурвица и Михайлова
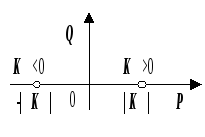
Исследование устойчивости методом Гурвица
Система
устойчива, если при
положительны все 3 определителя Гурвица
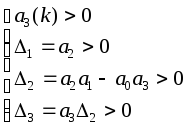
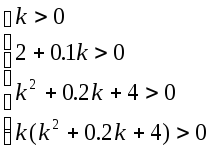
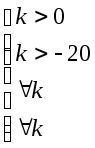
При
РС
k
устойчива
-1.5 -1.02 -1
Исследование устойчивости методом Михайлова
По критерию Михайлова система устойчива, если выполняются неравенства
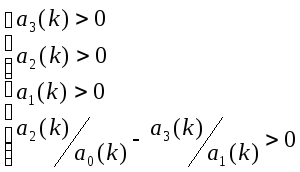
Из данного неравенства следуют 2 варианта:
1 вариант
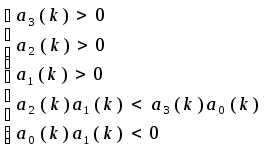
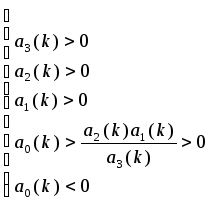Неравенство
несовместно
2 вариант
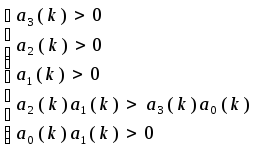
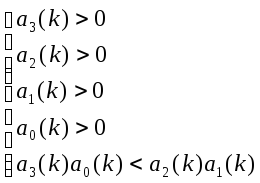
Такая же система неравенств, как и в критерии Гурвица, следовательно
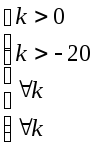
При
РС
k устойчива
-1.5 -1.02 -1
устойчива на гране устойчивости
не устойчива
Пункт №4
Получить
передаточную функцию
замкнутой единичной отрицательной
обратной связью системы.
Пункт №5
Исследовать устойчивость замкнутой системы от параметра методом Гурвица и Рауса и получить диапазоны устойчивых и неустойчивых значений параметра в классе вещественных чисел.
Метод Гурвица.
где
Необходимое условие
или
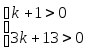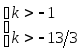или
или
k
-13/3 -1
Достаточное условие
-
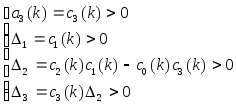
Г=
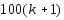
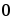
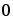
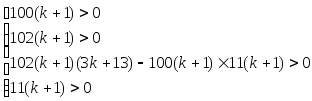
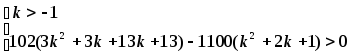
k
-1 0.285
Объединяя вместе необходимое и достаточное условие получаем:
или
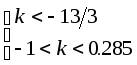
Система
не совместна
При
замкнутая система устойчива
2
Метод Рауса
Таблица Рауса
-
Вспомогательные коэффициенты
№
строки
Номер столбца
1
2
1
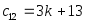
2
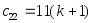
3
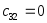
4
По критерию Рауса система устойчива если выполняются следующая система неравенств:
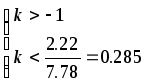
k
-1 0.285
При
замкнутая система устойчива
Пункт №6
Оформить набор значений параметра, включающий все граничные значения и по одному значению из каждого диапазона устойчивости и неустойчивости замкнутой системы.
Пункт №8
Выбрать
из диапазона устойчивости разомкнутой
системы конкретное значение параметра
и получить числовую передаточную функцию
для разомкнутой системы, с которой далее
будет вестись вся работа.
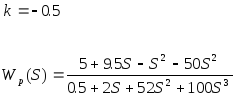
Пункт №7
Построить все частотные характеристики разомкнутой системы для каждого значения параметра из набора и использовать их для исследования устойчивости замкнутой системы от параметра методами Найквиста и Михайлова.
k=-1.5 По Найквисту ЗС не устойчива
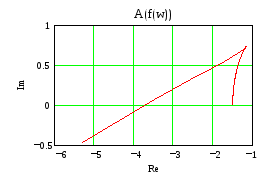
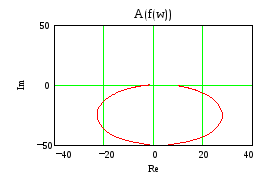
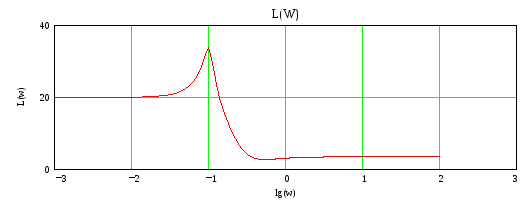
По Михаилову
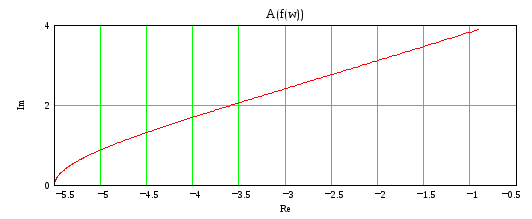
k=-1 По Найквисту ЗС на гране неустойчивости
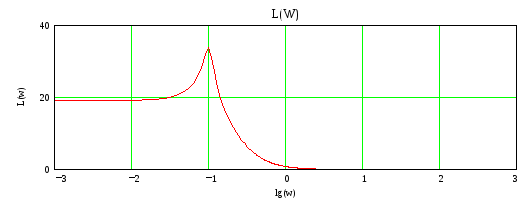
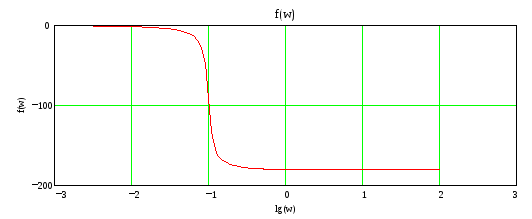
По Михаилову
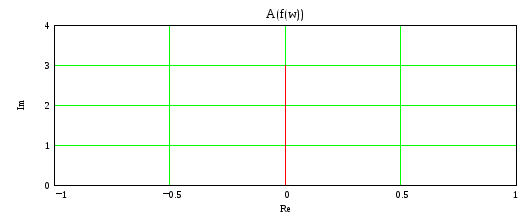
k=-0.5 По Найквисту ЗС устойчива
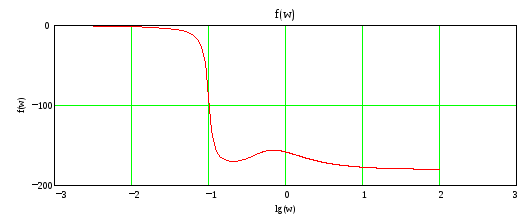
По Михаилову
k=0.285 По Найквисту ЗС на гране неустойчивости
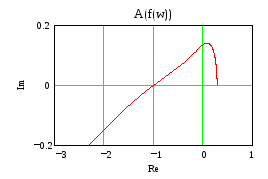
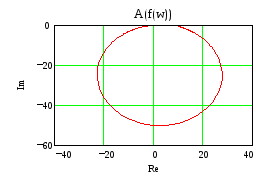
По Михаилову
По Михаилову
Пункт №9
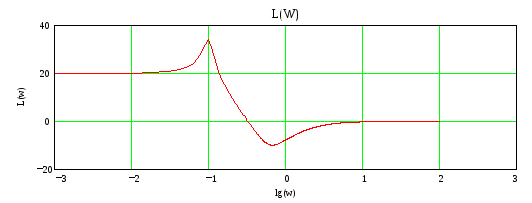
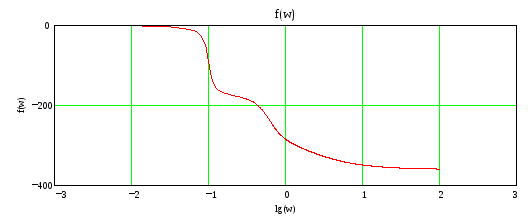
Получить оценки качества временных характеристик разомкнутой системы.
Установившееся значение
Начальное значение
Точность регулирования
Перерегулирование
Так
как
на отрезке
,
поэтому время регулирования или время
установления переходного процесса
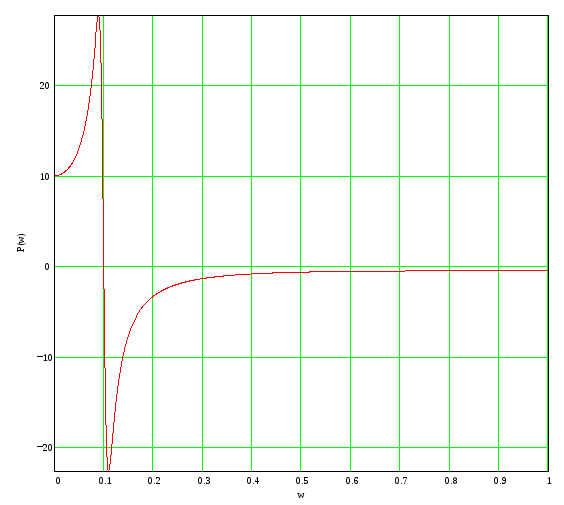
Пик
на частоте
свидетельствует о затухающих колебаниях
с частотой близкой к значению
или периодом
Время регулирования
Объединяя полученные решения
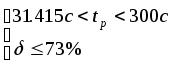
Пункт №10
Рассчитать частотными методами временные характеристики РС и сравнить их показатели качества с оценками полученными в пункте №9.
Импульсная характеристика:
Переходная характеристика:
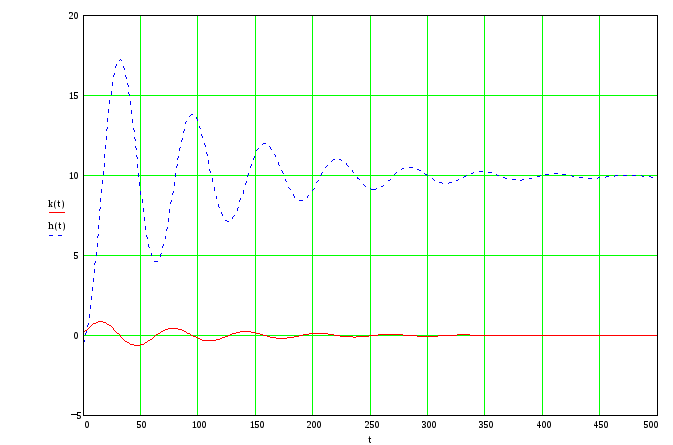
Оценки качества временных характеристик по переходной характеристике:
Начальное значение
Установившееся значение
Точность регулирования
Перерегулирование
Время быстродействия или регулирования
Частота и период затухания
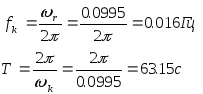
Объединяя полученные решения
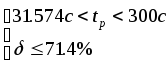
Оценки согласуются с оценками сделанными в пункте № 9
Пункт №11
Рассчитать частотными методами реакцию разомкнутой системы на нетиповое воздействие при нулевых начальных условиях.
Вид входного воздействия
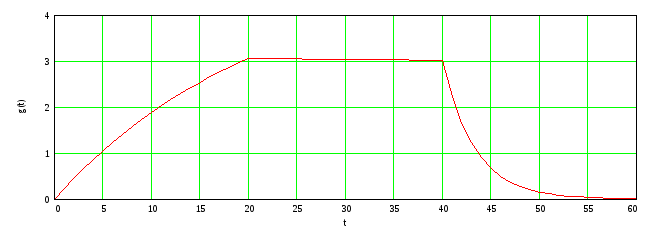
Переходная характеристика
Пункт №12
Рассчитать регулятор обеспечивающую нулевую статическую ошибку, имеющий перерегулирование не более 20% и быстродействие в 10 раз большее чем разомкнутая система.
Структурная схема замкнутой схемы с регулятором.
-
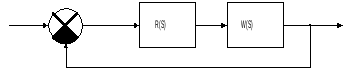
последовательный регулятор, который
необходимо рассчитать
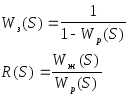
желаемая
передаточная функция системы
реальная
неизменяемая передаточная функция
Форма
сопрягающего участка логарифмической
амплитудной характеристики между
частотами
и
выбрана такой, для того чтобы обеспечить
необходимые запасы по фазе и по амплитуде.
Найдем графически частоты на которых происходит излом графика логарифмической амплитудно-частотно характеристики.
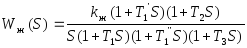
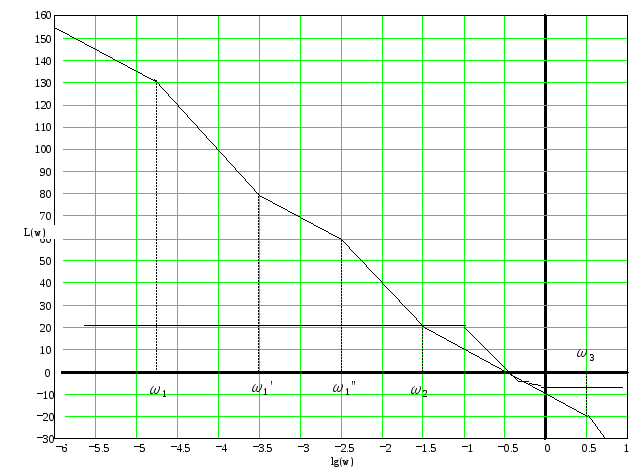
Расчет последовательного регулятора, ЛАЧХ, ЛФЧХ, импульсной и переходной
характеристик замкнутой системы с регулятором.
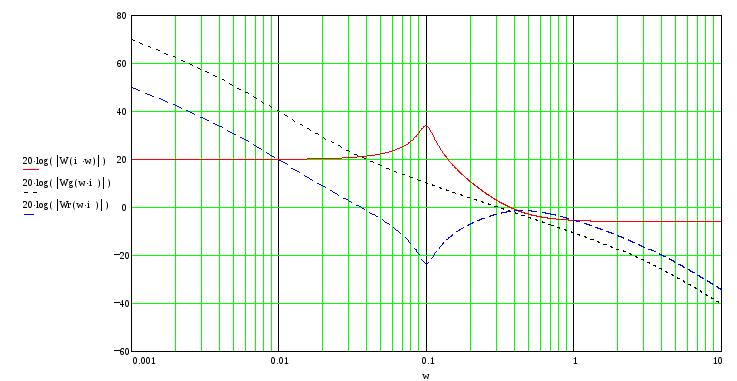
Импульсная характеристика замкнутой системы с регулятором
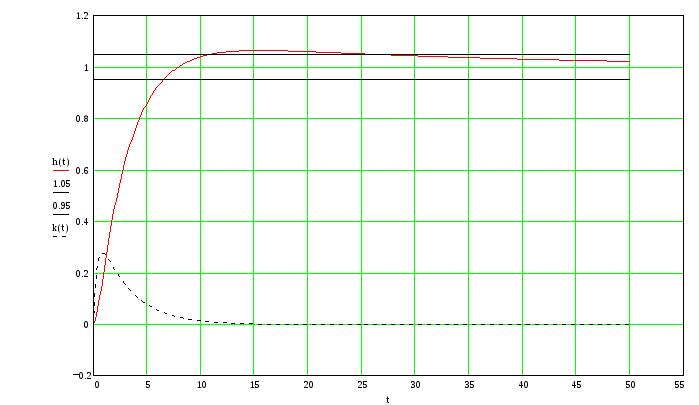
Переходная характеристика замкнутой системы с регулятором
Перерегулирование
Литература
-
Теория автоматического управления. Пол ред. А.А. Воронова
-
Теория автоматического управления. Пол ред. А.С. Шаталова
-
Никулин Е.А. Теория автоматического управления. Методические указания.