2.2. Метод определения минимально-безопасного расстояния (дистанции) между автомобилями

Введем некоторые определения, которые потребуются в дальнейшем.

Определение 1. Будем говорить, что столкновение автомобилей и на отрезке времени не произойдет, а отрезок времени будем называть безопасным (в смысле невозможности столкновения), если для любого из этого отрезка выполняется неравенство (2.1.15).

Определение 2. Момент времени будем называть моментом касания автомобилей и на отрезке времени , если и выполняется равенство

.

Определение 3. Момент касания будем называть опасным моментом касания, или моментом столкновения автомобилей и на отрезке времени , если выполняется условия: :

1) при

2); (2.2.1)

3) при .

Механический смысл неравенства (2.2.1) состоит в том, что после момента касания начинает происходить деформация элементов кузова автомобилей, поэтому расстояние между центрами масс автомобилей и начинает уменьшаться.

Определение 4. Момент касания будем называть безопасным моментом касания автомобилей и на отрезке времени , если выполняются условия: :

1) при

2); (2.2.2)

3) при .

Механический смысл этого определения состоит в том, что автомобиль , догнав и коснувшись передней кромкой переднего бампера задней кромки заднего бампера автомобиля в момент времени , или начнет двигаться с той же скоростью, что и автомобиль , или начнет отставать от автомобиля .

Отметим, что условия (2.2.2) совпадают с необходимым условием минимума функции на отрезке времени в момент времени =.

Определение 5. Выбранное начальное расстояние будем называть безопасным на отрезке времени для автомобилей и , если неравенство (2.1.15) выполняется для всех моментов времени из отрезка .

Безопасное начальное расстояние , вообще говоря, является функционалом от параметров движения автомобилей и , т. е. зависит от ускорений автомобилей на отрезке времени , начальных скоростей и , технического состояния, дорожных условий и т.д. Следует отметить, что если для заданного движения автомобилей мы нашли некоторое безопасное расстояние , то любое расстояние будет тоже безопасным. Так как множество безопасных расстояний S⁰=для рассматриваемых движений автомобилей и ограничено снизу нулем, то существует точная нижняя граница этого множества

=S⁰ (2.2.3)

такая, что любое является безопасным начальным расстоянием для заданных движений автомобилей и , а для любого автомобили и неизбежно столкнутся.

Определение 6. Наименьшее значение из множества S⁰, определенное равенством (2.2.3), будем называть минимально-безопасным начальным расстоянием и обозначать .

Если при движении автомобилей и водителю автомобиля , который находился в начальный момент времени на расстоянии от автомобиля , удается добиться того, что функция принимает на отрезке времени неотрицательные значения, т. е. выполняется неравенство (2.1.15), то в этом случае из равенства (2.1.13) следует, что

(2.2.4)

на рассматриваемом отрезке времени. Неравенство (2.2.4) означает согласно определению 1, что столкновение автомобилей и на этом отрезке времени не произойдет. Если же водителю автомобиля не удается добиться (вплоть до применения экстренного торможения) выполнения неравенства (2.2.4) в любой момент времени на отрезке , то столкновение автомобилей и необходимо произойдет. Это означает, что он неправильно выбрал начальное расстояние в начальный момент времени

Утверждение 1. Если при движении автомобилей и функция принимает неотрицательные значения на отрезке времени , то столкновение автомобилей и на этом отрезке времени не произойдет, а начальное безопасное расстояние может быть любым неотрицательным числом, т. е. минимально-безопасное расстояние .

Доказательство. Действительно, так как для , то в силу равенства (2.1.13) функция и, следовательно, согласно определению 1 столкновение автомобилей и не произойдет.

В этом случае начальное расстояние между автомобилями может быть любым , следовательно, .

Пусть движение автомобилей и таково, что функция принимает на отрезке времени как неотрицательные, так и отрицательные значения.

Утверждение 2. Если функция принимает на отрезке времени как отрицательные, так и неотрицательные значения, то минимально-безопасное расстояние для этого отрезка времени определяется равенством

(2.2.5)

Доказательство: Так как функция , определенная равенством (2.1.14), непрерывна и дифференцируема на отрезке времени , то она необходимо ограничена и достигает своей точной нижней границы при некотором значении , т. е.

, (2.2.6)

так как функция принимает и отрицательные значения на рассматриваемом отрезке. Покажем, что величина является минимально-безопасным начальным расстоянием на отрезке . Подставляя в равенстве (3.1.13) вместо значение функции , получим

для , так как из определения точной нижней границы следует

для .

Таким образом, получили, что начальное расстояние является безопасным. Покажем, что оно является минимально-безопасным начальным расстоянием для отрезка времени .

Допустим противное. Пусть существует безопасное : < и

(2.2.7)

для. Возьмем произвольное число , удовлетворяющее неравенству

или

.

Из равенства (2.2.6) и свойств точной нижней границы для выбранного >0 найдется

,

но тогда

<<,

т.е. , что противоречит нашему предположению о том, что является безопасным расстоянием, т.е. неравенству (2.2.7). Полученное противоречие и доказывает наше утверждение.

Доказанные утверждения дают практический метод нахождения минимально-безопасного начального расстояния между автомобилями и для заданного отрезка времени.

При экстренном торможении автомобиля для нахождения минимально-безопасного расстояния в качестве отрезка времени необходимо рассматривать отрезок времени , где время движения автомобиля до полной остановки.

Таким образом, для нахождения минимально-безопасного расстояния в случае, если функция может принимать на отрезке времени как положительные, так и отрицательные значения, необходимо:

1) найти все моменты времени подозрительные на экстремум, т.е. точки, в которых выполняется равенство

;

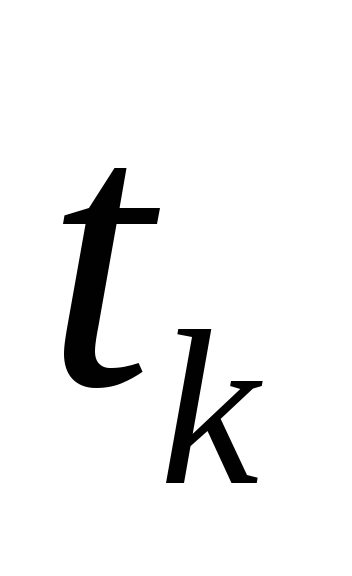
3. найти все точки (безопасные моменты касания), в которых функция 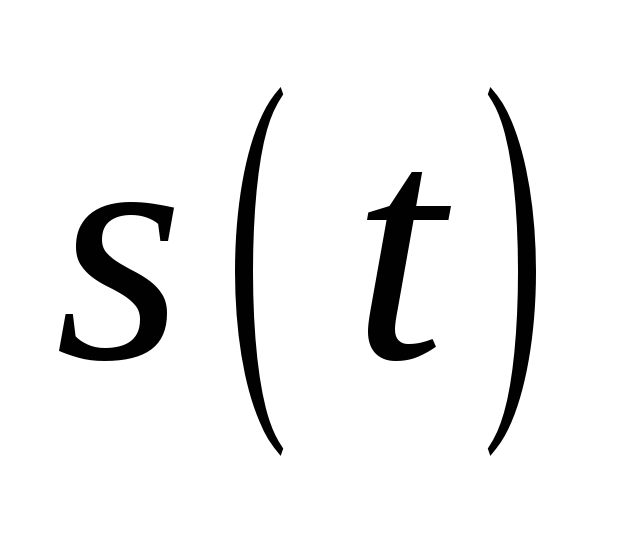достигает отрицательного минимума, тогда минимально-безопасное расстояние определяется равенством

,

если , и

,

если .

Если функция принимает только положительные значения, т.е. для всех , то в этом случае .

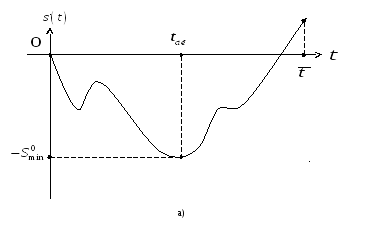
Геометрический смысл нахождения минимально-безопасного расстояния состоит в нахождении положительной величины (рис.2.2.1, а), б)), на

которую необходимо сдвинуть график функции вдоль оси вверх, чтобы график функции только касался оси и полностью лежал бы в первом

квадранте системы координат при .

Метод, основанный на доказанных утверждениях, позволяет в дальнейшем находить минимально-безопасное расстояние между автомобилями, дви-

0

Рис.2.2.1

жущимися в попутном направлении, при любом техническом состоянии автомобилей , и любых дорожных условиях.

39