
- •Введение
- •§1. Теоремы Ролля, Лагранжа, Коши
- •§2. Теоремы Лопиталя-Бернулли
- •§3. Формула Тейлора
- •§4. Исследование функций и построение графиков
- •4.1. Возрастание и убывание функций. Экстремумы
- •4.2. Нахождение наименьшего и наибольшего значений непрерывной функции на отрезке
- •4.3. Нахождение промежутков выпуклости и вогнутости графика функции, точек перегиба
- •4.4. Нахождение асимптот графика функции
- •4.5. Полное исследование функций и построение графиков
- •Использованная литература
4.4. Нахождение асимптот графика функции
Определение 9. Асимптотой графика функции называется прямая, к которой неограниченно приближается уходящая в бесконечность ветвь графика функции.
Нахождение вертикальных асимптот. Если
функция
![]() в точке
в точке
![]() непрерывна, то прямая
непрерывна, то прямая![]() не может быть асимптотой.
не может быть асимптотой.
Так
как элементарная функция непрерывна
в области существования, то у элементарной
функции вертикальные асимптоты могут
быть только на границе области
существования. Пусть
![]() - граничная точка области существования
элементарной функции
- граничная точка области существования
элементарной функции
![]() ,
тогда необходимо найти односторонние
пределы
,
тогда необходимо найти односторонние
пределы
![]() .
Если один из односторонних пределов
равен
.
Если один из односторонних пределов
равен
![]() ,
то прямая
,
то прямая
![]() является односторонней вертикальной
асимптотой. Если же лба односторонних
предела равны
является односторонней вертикальной
асимптотой. Если же лба односторонних
предела равны
![]() ,
то прямая
,
то прямая
![]() является двусторонней асимптотой.
является двусторонней асимптотой.
Уравнение
наклонной асимптоты записывается в
виде
![]() .
Параметры
.
Параметры
![]() и
и
![]() находятся по формулам:
находятся по формулам:
![]() .
.
Оказывается
при
![]() можно получить одну асимптоту, а при
можно получить одну асимптоту, а при
![]() другую асимптоту отличную от первой.
другую асимптоту отличную от первой.
Пример
16. Найти асимптоты графика функции
![]() .
.
Решение.
Данная функция является элементарной.
Область определения ее состоит из трёх
интервалов
![]() .
Граничными точками области определения
являются две точки
.
Граничными точками области определения
являются две точки
![]() и
и
![]() .
Найдём односторонние пределы в точках
.
Найдём односторонние пределы в точках
![]() .
.
![]() .
Прямая
.
Прямая
![]() не является асимптотой.
не является асимптотой.
![]() .
Прямая
.
Прямая
![]() является двухсторонней асимптотой.
является двухсторонней асимптотой.
Остаётся
выяснить наличие наклонных асимптот
![]() .
.
![]()
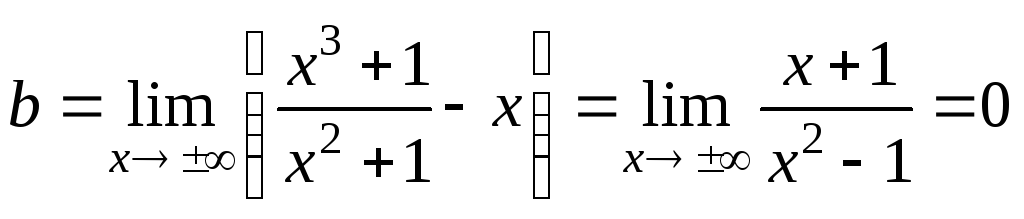
Таким
образом, прямая
![]() является асимптотой как при
является асимптотой как при
![]() ,
так и при
,
так и при
![]() .
.
Найти асимптоты графиков функций.
57.
![]() 58.
58.
![]() 59.
59.
![]() 60.
60.
![]() 61.
61.
![]()
4.5. Полное исследование функций и построение графиков
Приведём примерный план исследования функций.
-
Определить область существования функции. Область существования функции указывает точки оси аргумента, над которыми пройдёт кривая.
-
Найти точки пересечения графика функции с осями координат.
-
Исследовать функцию на периодичность. Для периодической функции достаточно построить график на промежутке длиной в период.
-
Исследовать функцию на четность и нечетность. Если функция четная или нечетная , то график функции достаточно построить при
 ,
а затем отобразить симметрично
относительно оси
,
а затем отобразить симметрично
относительно оси
 в случае чётной функции или относительно
начала координат в случае нечётной
функции.
в случае чётной функции или относительно
начала координат в случае нечётной
функции. -
Найти промежутки возрастания и убывания функции, точки экстремума.
-
Найти промежутки выпуклости и вогнутости графика функции, точки перегиба.
-
Определить асимптоты.
-
Все данные свести в таблицу и построить график.
-
Если полученные результаты не дают ясной картины поведения графика, то следует нанести ещё несколько точек кривой в тех местах, где течение графика менее ясно.
Пример 17. Построить график функции
![]() .
.
Решение.
-
Область существования функции
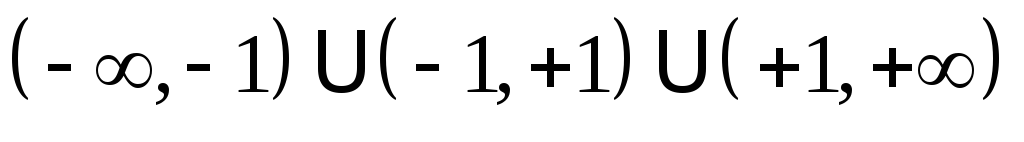 .
. -
График функции с осями координат не пересекается.
-
Функция не является периодической.
-
 .
Функция не является ни четной, ни
нечетной.
.
Функция не является ни четной, ни
нечетной. -
Найдем промежутки возрастания и убывания функции, точки экстремума.
![]() .
.
 .
Критические точки
.
Критические точки
![]()
Имеем:
-

- график функции возрастает;

- график функции возрастает;

- график функции убывает;

- график функции убывает;

- график функции возрастает.
При переходе через точку
![]() производная меняет знак с + на
производная меняет знак с + на
![]() ,
поэтому функция в точке
,
поэтому функция в точке
![]() имеет максимум,
имеет максимум,
![]() .
При переходе через точку
.
При переходе через точку
![]() производная меняет знак с
производная меняет знак с
![]() на +, функция в точке
на +, функция в точке
![]() имеет минимум,
имеет минимум,
![]() .
.
-
Найдём промежутки выпуклости и вогнутости графика функции, точки перегиба.
![]() .
При
.
При
![]() - график функции выпуклый;
- график функции выпуклый;
![]() - график функции выпуклый;
- график функции выпуклый;
![]() - график функции вогнутый.
- график функции вогнутый.
-
Асимптоты для данной функции найдены в примере 16. Прямая
 - двухстороння вертикальная асимптота.
- двухстороння вертикальная асимптота.
Полученные результаты запишем в таблице.
|
|
|
|
|
0 |
|
1 |
|
2 |
|
|
|
+ |
не сущ |
+ |
0 |
|
не сущ |
|
0 |
+ |
|
|
|
не сущ |
|
|
|
не сущ |
+ |
+ |
+ |
|
|
|
не сущ |
|
max
|
|
не сущ |
|
min 3 |
|

Рис. 2
Исследовать и построить графики следующих функций.
|
62.
|
69.
|
|
63.
|
70.
|
|
64.
|
71.
|
|
65.
|
72.
|
|
66.
|
73.
|
|
67.
|
74.
|
|
68.
|
75.
|
