
- •Введение
- •§1. Теоремы Ролля, Лагранжа, Коши
- •§2. Теоремы Лопиталя-Бернулли
- •§3. Формула Тейлора
- •§4. Исследование функций и построение графиков
- •4.1. Возрастание и убывание функций. Экстремумы
- •4.2. Нахождение наименьшего и наибольшего значений непрерывной функции на отрезке
- •4.3. Нахождение промежутков выпуклости и вогнутости графика функции, точек перегиба
- •4.4. Нахождение асимптот графика функции
- •4.5. Полное исследование функций и построение графиков
- •Использованная литература
4.2. Нахождение наименьшего и наибольшего значений непрерывной функции на отрезке
Теорема 5. Если функция непрерывна на
отрезке
![]() ,
то она на этом отрезке достигает свои
наименьшее и наибольшее значения.
,
то она на этом отрезке достигает свои
наименьшее и наибольшее значения.
Теорема 6. Если функция
![]() достигает наименьшее (наибольшее)
значение в точке
достигает наименьшее (наибольшее)
значение в точке
![]() внутри отрезка
внутри отрезка
![]() ,
то
,
то
![]() либо равно 0 либо не существует, т.е.
либо равно 0 либо не существует, т.е.
![]() является критической точкой.
является критической точкой.
Отсюда следует, что функция принимает наименьшее (наибольшее) значение либо в критической точке, либо на концах данного отрезка.
Пример 14. Найти наименьшее и наибольшее
значение функции
![]() на отрезке
на отрезке
![]() .
.
Решение.
![]() .
Точка
.
Точка
![]() не является критической, т.к. она является
концом отрезка
не является критической, т.к. она является
концом отрезка
![]() .
Теперь найдём значение функции в
критической точке
.
Теперь найдём значение функции в
критической точке
![]() и на концах отрезка, т.е. в точках
и на концах отрезка, т.е. в точках
![]() и
и
![]() .
.
![]() .
.
Среди полученных значений выберем наименьшее и наибольшее. Они и будут соответственно наименьшим и наибольшим значениями функции на данном отрезке.
![]() - наименьшее значение
- наименьшее значение
![]() - наибольшее значение
- наибольшее значение
Найти наименьшее и наибольшее значения функции на указанных отрезках (если отрезок не указан, то во всей области определения).
|
38.
|
40.
|
|
39.
|
41.
|
Доказать следующие неравенства
|
42.
|
44. (4.29) ----//---- |
46. (4.35) |
|
43. (4.28) (Ефимов) |
45. (4.31) |
|
47. На графике
![]() найти точку, расстояние от которой до
точки
найти точку, расстояние от которой до
точки
![]() будет наименьшим. Чему равно это
расстояние?
будет наименьшим. Чему равно это
расстояние?
48.
![]() .
.
49. Какую наибольшую площадь может иметь
прямоугольный треугольник, одна вершина
которого лежит в начале координат,
другая – на графике функции
![]() ,
а вершина прямого угла на оси
,
а вершина прямого угла на оси
![]() ?
?
4.3. Нахождение промежутков выпуклости и вогнутости графика функции, точек перегиба
О пределение
6. График функции называется выпуклым
(вогнутым) в точке, если касательная,
проведённая к кривой в этой точке, лежит
над графиком (под графиком) в некоторой
окрестности данной точки.
пределение
6. График функции называется выпуклым
(вогнутым) в точке, если касательная,
проведённая к кривой в этой точке, лежит
над графиком (под графиком) в некоторой
окрестности данной точки.
Определение 7. График функции называется
выпуклым (вогнутым) на интервале
![]() ,
если график функции выпуклый в каждой
точке этого интервала.
,
если график функции выпуклый в каждой
точке этого интервала.
Определение 8. Пусть
![]() непрерывна в точке
непрерывна в точке
![]() .
Точка
.
Точка
![]() называется точкой перегиба, если при
переходе через эту точку график функции
меняет выпуклость на вогнутость или
вогнутость на выпуклость.
называется точкой перегиба, если при
переходе через эту точку график функции
меняет выпуклость на вогнутость или
вогнутость на выпуклость.
Теорема 7. Если функция дважды
дифференцируема и
![]() (
(![]() )
на интервале
)
на интервале
![]() ,
то её график является выпуклым (вогнутым)
на
,
то её график является выпуклым (вогнутым)
на
![]() .
.
Часто область определения функции можно
разбить на интервалы, в каждом из которых
![]() имеет постоянный знак. Эти интервалы
ограничены точками, в которых
имеет постоянный знак. Эти интервалы
ограничены точками, в которых
![]() или не существует.
или не существует.
Теорема 8. Пусть
![]() дважды дифференцируема в некоторой
окрестности точки
дважды дифференцируема в некоторой
окрестности точки
![]() ,
причём
,
причём
![]() или
или
![]() не существует. Если при переходе через
точку
не существует. Если при переходе через
точку
![]()
![]() меняет знак, то
меняет знак, то
![]() - точка перегиба.
- точка перегиба.
Пример 15. Найти промежутки выпуклости,
вогнутости и точки перегиба функции
![]() .
.
Решение.
![]()
-


0

1
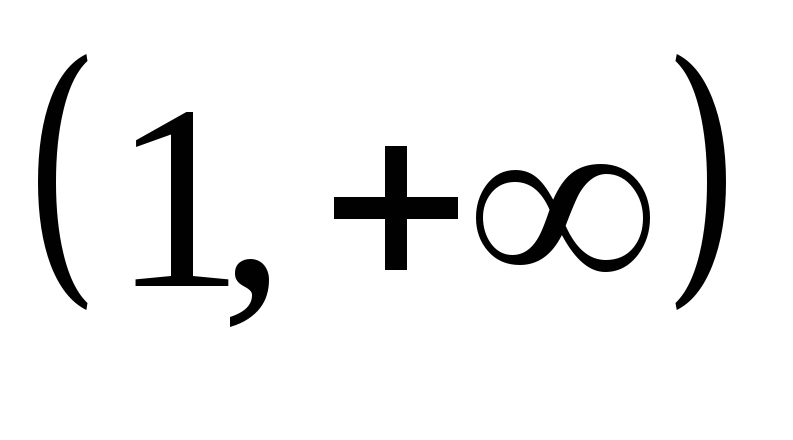

+
0

0
+


т. перегиба
т. перегиба

Таким
образом, в промежутках
![]() ,
,
![]() график функции вогнутый, а в промежутке
график функции вогнутый, а в промежутке
![]() - выпуклый; точки
- выпуклый; точки
![]() являются точками перегиба.
являются точками перегиба.
Найти интервалы выпуклости и вогнутости графика функции, точки перегиба.
|
50.
|
53.
|
56.
|
|
51.
|
54.
|
|
|
52.
|
55.
|
|
