Тест IV

1. Булевой функцией от n переменных называется функция, определенная на множестве всех двоичных наборов длины n и принимающая на каждом из них значение.

а) 0; б) 1; в) 0 или 1; г) любые целые;

2. Булева функция называется монотонной, если из ху следует

а) б) >; в) ; г)< ;

3. Выражение 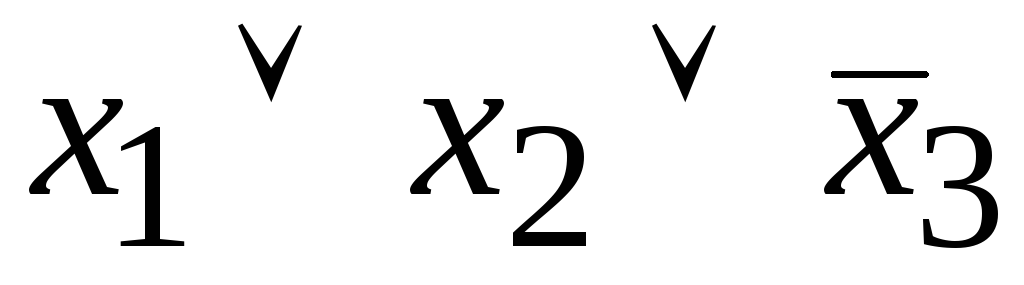называют

а) элементарной дизъюнкцией; б) элементарной конъюнкцией.

4. Результатом упрощения д.н.ф. является форма:

а) б) ; в) .

5. Функцией, двойственной к функции , является

а) б) в)

Тест V

1) Для нахождения (48,27) алгоритма Евклида выполнит

а) 2 шага; б) 3 шага; в) 4 шага.

2) Наибольший общий делитель многочленов x²-3x+2 и x²-4x+3 равен

а) x+1; б) x-1; в) x²-1.

3) Применима ли к слову 1¹⁰⁰ машина Тьюринга, задаваемая программой

q₁1 → q₁0R

q₁0 → q₂1L

q₂1 → q₀1C

q₂0 → q₁0R

а) применима; б) не применима.

4) Среди трех монет одна фальшивая. В результате какого наименьшего числа взвешиваний можно определить фальшивую монету

а) одного; б) двух; в) трех.

Рекомендуемая литература

2.3. Основная:

1. Шапорев С.Д. Матемаьтческая логика. Курс лекций и практических занятий. – СПб.: БХВ – Петербург, 2005.- 416 с.: ил.

2. Шелупанов А.А., Зюзьков В.М. Математическая логика и теория алгоритмов. – М.: Горячая линия – Телеком, 2007.- 176 с.

3. Игошин В.И. Задачи и упражнения по математической логике и теории алгоритмов. – М.: Академия, 2007.-304 с.

4. Лавров И.А Математическая логика. – М.: Академия, 2006. – 240 с.

2.4. Дополнительная:

1. Колмагоров А.Н., Драгалин А.Г. Математическая логика. – М.: Едиториал УРСС 2004.- 240 с.

2. Успенский В.А., Верещагин Н.К., Плиско В.Е. Вводный курс математической логики. – 2-е изд. – М.: Физматлит, 2002. – 128 с.

3. Лавров И.А. Максимова Л.Л. Задачи по теории множеств математической логики и теории алгоритмов . – 4-е изд. М.: Физматлит, 2001. – 256 с

4