
- •Раздел II. Основы векторной алгебры
- •Глава 3. Векторы
- •3.1. Основные понятия
- •3.2. Линейные операции над векторами
- •3.3. Координаты вектора
- •Нахождение скалярного произведения через координаты векторов
- •Приложения скалярного произведения векторов
- •3.5. Векторное произведение векторов
- •Метод координат
- •§ 1. Координатная ось. Декартовы координаты на плоскости и в пространстве
- •Операции над векторами
Метод координат
В элементарной (школьной) геометрии изучаются свойства прямолинейных фигур и окружности (в разделе планиметрия), а также прямые и плоскости в пространстве, многогранники и круглые тела — цилиндр, конус, шар (в разделе стереометрия). Основную роль при этом играют построения, а вычислениям отводится роль вспомогательная. Выбор того или иного построения для каждого конкретного случая требует обычно индивидуального подхода и соответствующей изобретательности, что и составляет основную трудность при решении задач методами элементарной геометрии.
Аналитическая геометрия и была призвана устранить эти трудности и создать единый метод решения различных геометрических задач. Поставленная цель была достигнута разработкой координатного метода, в котором основную роль играют вычисления, выполняемые по заданным формулам, а построения имеют вспомогательное значение.
Необходимые предпосылки для создания метода координат были подготовлены еще трудами древнегреческих математиков, в особенности Аполлония Пергского (ок. 260—170 до н. э.). Однако систематическое развитие этот метод получил в первой половине XVII века в работах Рене Декарта и Пьера Ферма.
Рене Декарт (Rene Descartes, 1596—1650) — знаменитый французский философ, математик, физик и физиолог. Родился в г. Лаэ (департамент Турень) в дворянской семье. В 1629 г. поселился в Голландии, где написал большую часть своих работ. Умер в Стокгольме, куда переехал в 1649 г.
В физике Декарт установил закон преломления света на границе двух сред (который несколько раньше и независимо от него был сформулирован В. Снеллиусом), пояснил образование радуги. Ему же принадлежит формулировка закона сохранения количества движения (в скалярной форме) и разработка механистической гипотезы образования тел Солнечной системы. В области физиологии Декарту принадлежит большое число экспериментов и ряд плодотворных научных идей, в частности, он первым ввел понятие о рефлексе.
В 1637 г. Декарт издал большой философский трактат «Рассуждение о методе. С приложениями: Диоптрика, Метеоры, Геометрия» (русский перевод, Гостехиздат, М., 1953), в котором, в частности, систематически изложен метод прямолинейных координат, введена удобная алгебраическая символика, сохранившаяся до наших дней, выполнена классификация кривых на алгебраические и трансцендентные, а также даны способы построения касательных и нормалей к плоским алгебраическим кривым. Благодаря этой работе, которая оказала большое влияние на дальнейшее развитие математики, Декарта, наряду с его не менее знаменитым соотечественником Ферма (который раньше и более последовательно, чем Декарт, разработал метод координат, но работы Ферма, в том числе и по аналитической геометрии, были опубликованы только в 1679 г. после его смерти), и считают основоположником аналитической геометрии, а 1637 год — годом ее зарождения.
Перейдём к изложению метода координат.
§ 1. Координатная ось. Декартовы координаты на плоскости и в пространстве
1. Координатная ось. Вещественные числа изображают геометрически точками прямой линии. Для этого на прямой линии (которую обычно чертят горизонтально) отмечают две точки: одну, изображающую число 0, и другую (обычно справа от первой), изображающую число 1. Отрезок 01 принимают за единицу масштаба для измерения длин на оси. Выбор eгo находится в нашем распоряжении. Но как только выбор сделан, каждое вещественное число изображается концом отрезка, измеряемого в указанном масштабе абсолютной величиной этого числа и откладываемого от точки О в сторону точки 1 (вправо), если число положительно, или в противоположную сторону (влево), если число отрицательно. Направление от точки 0 к точке 1 называют положительным, противоположное направление — отрицательным (обычно положительное направление отмечается стрелкой).
Прямая, на которой одно из двух возможных направлений выбрано в качестве положительного, называется ориентированной прямой или осью. Таким образом, для изображения вещественных чисел служит ось, на которой выбраны точка 0 („начало отсчета", или начало координат) и единица масштаба; такая ось называется координатной осью (или числовой прямой). Полупрямая, идущая от точки 0 в положительном направлении, называется положительной полуосью; полупрямая, идущая от точки 0, в противоположном направлении, — отрицательной полуосью. Отрезок, соединяющий начало координат с точкой координатной оси, называется координатным отрезком этой точки.
Каждая точка координатной оси изображает в указанном смысле некоторое вещественное число. Это число называют координатой точки. Таким образом, координата точки равна (измеренной в выбранном масштабе) длине ее координатного отрезка, взятой со знаком плюс, если точка лежит на положительной полуоси, или со знаком минус, если точка лежит на отрицательной полуоси. Начало координат имеет координату нуль. Положение каждой точки координатной оси вполне определяется заданием ее координаты.
Таким образом между совокупностью всех точек прямой и совокупностью всех вещественных чисел устанавливается взаимно однозначное соответствие: каждому вещественному числу соответствует одна и только одна изображающая его точка прямой, и каждой точке прямой соответствует одно и только одно вещественное число— ее координата. Геометрическое изображение чисел точками прямой доставляет одновременно способ задавать положение точек прямой числами.
 2.
Декартовы координаты на плоскости. Для
того чтобы задавать числами положение
точек плоскости, на плоскости выбирают
две координатные оси, пересекающиеся,
вообще говоря, под произвольным углом
(разумеется, отличным от 0° и 180°).
Масштабные единицы на этих осях могут
быть выбраны различные. Кроме них, для
измерения длин на плоскости выбирается
общая „абсолютная масштабная единица",
которой, в частности, измеряются и длины
масштабных единиц на осях. В качестве
начала отсчета на обеих осях берется
точка их пересечения О (начало координат:
от латинского origo – начало; отсюда и
«оригинал», т.е. первоисточник, начало).
Одну из координатных осей называют
осью абсцисс (осью х), другую -осью ординат
(осью у), Пусть М— какая-нибудь точка
на плоскости. Проведем через М прямые,
параллельные координатным осям (рис.).
Прямая, параллельная оси ординат,
пересечет ocь абсцисс в некоторой
точке М
2.
Декартовы координаты на плоскости. Для
того чтобы задавать числами положение
точек плоскости, на плоскости выбирают
две координатные оси, пересекающиеся,
вообще говоря, под произвольным углом
(разумеется, отличным от 0° и 180°).
Масштабные единицы на этих осях могут
быть выбраны различные. Кроме них, для
измерения длин на плоскости выбирается
общая „абсолютная масштабная единица",
которой, в частности, измеряются и длины
масштабных единиц на осях. В качестве
начала отсчета на обеих осях берется
точка их пересечения О (начало координат:
от латинского origo – начало; отсюда и
«оригинал», т.е. первоисточник, начало).
Одну из координатных осей называют
осью абсцисс (осью х), другую -осью ординат
(осью у), Пусть М— какая-нибудь точка
на плоскости. Проведем через М прямые,
параллельные координатным осям (рис.).
Прямая, параллельная оси ординат,
пересечет ocь абсцисс в некоторой
точке М![]() ;
прямая, параллельная оси абсцисс,
пересечет ось ординат в некоторой
точке Му. Пусть х — координата точки
Мх на оси абсцисс и у - координата точки
Му на оси ординат, причем отрезки
ОМх и ОМу измерены, каждый, масштабной
единицей, принятой на соответствующей
оси. Очевидно, положение точки М в
плоскости вполне определяется
положением точек Мх и Му на координатных
осях, т. е. числами х и у. Эти числа
называются декартовыми координатами
точки М, при этом х — абсциссой, a y —
ординатой. Параллелограмм ОМхММу,
ограниченный осями координат и
параллельными им прямыми, проходящими
через точку М, называется координатным
параллелограммом точки М; его стороны
(и в частности отрезки ОМх , ОМу)
называются координатными отрезками
точки М.
;
прямая, параллельная оси абсцисс,
пересечет ось ординат в некоторой
точке Му. Пусть х — координата точки
Мх на оси абсцисс и у - координата точки
Му на оси ординат, причем отрезки
ОМх и ОМу измерены, каждый, масштабной
единицей, принятой на соответствующей
оси. Очевидно, положение точки М в
плоскости вполне определяется
положением точек Мх и Му на координатных
осях, т. е. числами х и у. Эти числа
называются декартовыми координатами
точки М, при этом х — абсциссой, a y —
ординатой. Параллелограмм ОМхММу,
ограниченный осями координат и
параллельными им прямыми, проходящими
через точку М, называется координатным
параллелограммом точки М; его стороны
(и в частности отрезки ОМх , ОМу)
называются координатными отрезками
точки М.
Ч тобы
указать, что точка М имеет координаты
х и у пишут: М(х,у); при этом абсциссу
помещают на первом месте, ординату - на
втором. Точку с абсциссой х и ординатой
у записывают также символом (х, у). Чтобы
построить точку (х, у), нужно на оси
абсцисс взять точку с координатой х и
провести через нее прямую, параллельную
оси ординат, далее, на оси ординат взять
точку с координатой у и провести через
нее прямую, параллельную оси абсцисс;
пересечение этих двух прямых и будет
точкой (х,у). Таким образом, каждой точке
плоскости соответствует вполне
определенная упорядоченная пара
вещественных чисел (указано, какое из
них первое, а какое — второе); и обратно,
каждой упорядоченной паре вещественных
чисел соответствует вполне определенная
точка плоскости. Иными словами, между
совокупностью всех точек плоскости и
совокупностью всех упорядоченных пар
вещественных чисел установлено взаимно
однозначное соответствий. Начало
координат О имеет координаты 0, 0. У всех
точек, лежащих на оси абсцисс, ординаты
равны нулю, у всех точек, лежащих на оси
ординат, абсциссы равны нулю; первые
имеют вид (х, 0), вторые — вид (0, у). Угол,
заключенный между положительными
полуосями х и у, называется первым
координатным углом; угол, заключенный
между положительной полуосью у и
отрицательной полуосью х, — вторым
координатным углом; угол, заключенный
между отрицательной полуосью х и
отрицательной полуосью у, —третьим
координатным углам; наконец, угол,
заключенный между отрицательной полуосью
у и положительной полуосью x, — четвертым
координатным углом.
тобы
указать, что точка М имеет координаты
х и у пишут: М(х,у); при этом абсциссу
помещают на первом месте, ординату - на
втором. Точку с абсциссой х и ординатой
у записывают также символом (х, у). Чтобы
построить точку (х, у), нужно на оси
абсцисс взять точку с координатой х и
провести через нее прямую, параллельную
оси ординат, далее, на оси ординат взять
точку с координатой у и провести через
нее прямую, параллельную оси абсцисс;
пересечение этих двух прямых и будет
точкой (х,у). Таким образом, каждой точке
плоскости соответствует вполне
определенная упорядоченная пара
вещественных чисел (указано, какое из
них первое, а какое — второе); и обратно,
каждой упорядоченной паре вещественных
чисел соответствует вполне определенная
точка плоскости. Иными словами, между
совокупностью всех точек плоскости и
совокупностью всех упорядоченных пар
вещественных чисел установлено взаимно
однозначное соответствий. Начало
координат О имеет координаты 0, 0. У всех
точек, лежащих на оси абсцисс, ординаты
равны нулю, у всех точек, лежащих на оси
ординат, абсциссы равны нулю; первые
имеют вид (х, 0), вторые — вид (0, у). Угол,
заключенный между положительными
полуосями х и у, называется первым
координатным углом; угол, заключенный
между положительной полуосью у и
отрицательной полуосью х, — вторым
координатным углом; угол, заключенный
между отрицательной полуосью х и
отрицательной полуосью у, —третьим
координатным углам; наконец, угол,
заключенный между отрицательной полуосью
у и положительной полуосью x, — четвертым
координатным углом.
3. Правая и левая системы координат на плоскости.
На рис. изображены два типа взаимного расположения координатных осей на плоскости. Если мы представим себя в роли наблюдателя, стоящего в начале координат и обращенного в сторону положительной полуоси х, то в случае а) ось у будет идти справа налево,
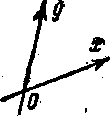 а)
а)
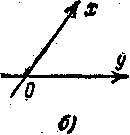
Рис.
а в случае б) — слева направо; В первом случае координатную систему называют правой, во втором левой. Вообще, упорядоченную пару пересекающихся направлений на плоскости называют правой, если второе направление пересекает первое справа налево (по отношению к наблюдателю, обращенному в сторону первого направления), и левой, если второе направление пересекает первое слева направо. Для того чтобы, поворачивая на наименьший угол, совместить первое направление со вторым, нужно в случае правой пары вращать его против часовой стрелки, а в случае левой пары — по часовой стрелке (черт. 5). Заметим, что, сравнивая направления осей на рис, мы представляли себя находящимися с той стороны плоскости, в которую обращен чертеж. Если бы мы перевернули страницу и посмотрели на рис на свет, то ориентации координатных систем переменились бы на обратные: правая представилась бы как левая, а левая — как правая.
4. Декартовы координаты в пространстве
Совершенно аналогично вводятся координаты в пространстве. А именно, берутся три координатные оси, пересекающиеся в одной точке и не лежащие в одной плоскости. Масштабные единицы на осях, вообще говоря, могут быть опять выбраны различные. Кроме них, для измерения всех длин в пространстве выбирается общая «абсолютная масштабная единица», которой, в частности, измеряются и длины масштабных единиц на осях. В качестве начала отсчета на всех трех осях берется точка их пересечения О (начало координат). Одну из координатных осей называют осью абсцисс (осью х), другую — осью ординат (осью у) и третью — осью аппликат (осью z). Плоскость, проходящая через оси х и у, называется координатной плоскостью ху, плоскость, проходящая через оси у и z,—координатной плоскостью уz и плоскость, проходящая через оси х и z, — координатной плоскостью хz. Для того чтобы задать числами положение точки М в пространстве, проводят через эту точку плоскости, параллельные координатным плоскостям. Плоскость, параллельная координатной плоскости уz, пересечет ось абсцисс в некоторой точке Мх; плоскость, параллельная координатной плоскости xz, пересечет ось ординат в некоторой точке Му; плоскость, параллельная координатной плоскости ху, пересечет ось аппликат в некоторой точке Мz. Пусть х, у, z— координаты точек Мх, Му, Мz на соответствующих осях. Положение точки М вполне определяется заданием чисел х, у, z. Эти числа называются декартовыми координатами точки М, при этом х — абсциссой, у — ординатой и z — аппликатой. Параллелепипед OMxMyMzABCM, высекаемый координатными плоскостями и параллельными им плоскостями, проходящими через точку М, называется координатным параллелепипедом точки М; его ребра (и в частности отрезки ОМх, OMy, OMz) называются координатными отрезками точки М. Чтобы указать, что точка М имеет координаты х, у и z, пишут: M{x,y,z); при этом абсциссу помещают на первом месте, ординату — на втором и аппликату — на третьем. Точку с абсциссой х, ординатой у и аппликатой z записывают также символом (х,у, z). Таким образом, каждой точке пространства соответствует вполне определенная упорядоченная тройка вещественных чисел; обратно, каждой упорядоченной тройке вещественных чисел соответствует вполне определенная точка пространства. Иными словами, между совокупностью всех точек пространства и совокупностью всех упорядоченных троек вещественных чисел установлено взаимно однозначное соответствие. Начало координат О имеет координаты 0, 0, 0. Точки оси абсцисс имеют вид (х, 0, 0), точки оси ординат—вид(0, у, 0), точки оси аппликат — вид (0,0, z). Точки координатной плоскости ху имеют вид (х, у, 0), точки координатной плоскости yz — вид (0, у, z), точки координатной плоскости xz — вид (х, 0, z). Координатные плоскости разбивают все пространство на восемь трехгранных углов.
5. Правая и левая системы координат в пространстве. На рис. изображены два типа взаимного расположения координатных осей в пространстве. Представим себя в роли наблюдателя, стоящего на плоскости ху с той ее стороны, в которую обращена ось z, и обращенного в сторону положительного направления оси х. Тогда в случае, изображенном на черт. 7, ось у будет, идти справа налево и система координат на плоскости ху будет представляться нам как правая, а в случае, изображенном на черт, 8, ось у будет идти слева направо и система координат на плоскости ху будет представляться нам как левая. В первом случае координатную систему хуz называют правой, во втором — левой.
В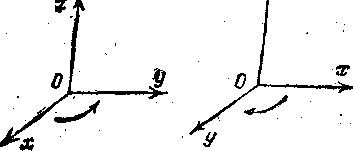 случае плоскости обычно пользуются
правой системой координат; при этом ocь
х чертят горизонтально и положительным
направлением на ней считают направление
слева направо; тогда положительным
направлением на оси у является направление
снизу вверх. В случае пространства
пользуются и той и другой системой
координат; мы будем пользоваться
преимущественно правой.
случае плоскости обычно пользуются
правой системой координат; при этом ocь
х чертят горизонтально и положительным
направлением на ней считают направление
слева направо; тогда положительным
направлением на оси у является направление
снизу вверх. В случае пространства
пользуются и той и другой системой
координат; мы будем пользоваться
преимущественно правой.
6. Общие декартовы; косоугольные и прямоугольные координаты. Описанные координаты — как на плоскости, так и в пространстве — называются общими декартовыми координатами. Если масштабные единицы на осях совпадают с выбранной абсолютной масштабной единицей, но углы между осями — не все прямые, то получаем так называемые косоугольные координаты, которыми много пользовались в некоторых прежних курсах аналитической геометрии; мы ими пользоваться совсем не будем. Если, кроме того оси взять взаимно перпендикулярными, то получатся прямоугольные координаты, наиболее часто употребляемые в практике.
Т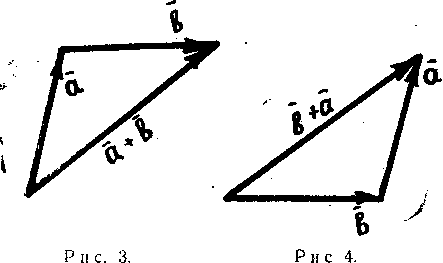 аким
образом, прямоугольными координатами
называются декартовы координаты,
удовлетворяющие двум условиям: 1)
координатные оси взаимно перпендикулярны
и 2) масштабные единицы на осях совпадают
с абсолютной единицей измерения длин.
В наименовании этих координат
прямоугольными отражено только первое
из этих двух условий.
аким
образом, прямоугольными координатами
называются декартовы координаты,
удовлетворяющие двум условиям: 1)
координатные оси взаимно перпендикулярны
и 2) масштабные единицы на осях совпадают
с абсолютной единицей измерения длин.
В наименовании этих координат
прямоугольными отражено только первое
из этих двух условий.
Сложение векторов
Пусть
![]() и
и
![]() —
два произвольных вектора. Приложим
вектор
—
два произвольных вектора. Приложим
вектор
![]() к концу вектора
к концу вектора
![]() ,
то есть совместим начало вектора
,
то есть совместим начало вектора
![]() с концом вектора
с концом вектора
![]() .
Тогда вектор, идущий из начала вектора
.
Тогда вектор, идущий из начала вектора
![]() в конец вектора
в конец вектора
![]() называется суммой векторов
называется суммой векторов
![]() и
и
![]() и обозначается
и обозначается
![]() +
+
![]() .
Такой способ построения суммы двух
векторов называют «правилом
треугольника» (рис. ).
.
Такой способ построения суммы двух
векторов называют «правилом
треугольника» (рис. ).
Если начало вектора
![]() совместить с концом вектора
совместить с концом вектора
![]() (рис.), то вектор, идущий из начала вектора
(рис.), то вектор, идущий из начала вектора
![]() в конец вектора
в конец вектора
![]() ,
будет вектором суммы
,
будет вектором суммы
![]() +
+
![]() .
.
Чтобы получить вектор суммы
![]() +
+
![]() можно воспользоваться также «правилом
параллелограмма». В этом случае векторы
можно воспользоваться также «правилом
параллелограмма». В этом случае векторы
![]() и
и
![]() приводят к общему началу, строят
параллелограмм на векторах слагаемых,
и тогда вектор, выходящий из того же
начала и совпадающий по длине и направлению
с диагональю построенного параллелограмма
будет искомым вектором суммы (рис. ).
приводят к общему началу, строят
параллелограмм на векторах слагаемых,
и тогда вектор, выходящий из того же
начала и совпадающий по длине и направлению
с диагональю построенного параллелограмма
будет искомым вектором суммы (рис. ).
Как видно, сумма двух векторов обладает
переместительным свойством, то есть
![]() +
+
![]() =
=
![]() +
+
![]() .
.
Понятие суммы двух векторов можно
обобщить на случай любого конечного
числа слагаемых. Пусть, например, даны
три вектора
![]() ,
,
![]() и
и
![]() и требуется найти их сумму
и требуется найти их сумму
![]() +
+
![]() +
+
![]() .
Искомый вектор можно получить,
последовательно применяя правило
треугольника:
.
Искомый вектор можно получить,
последовательно применяя правило
треугольника:
прикладываем вектор
![]() к вектору
к вектору
![]() и получаем вектор
и получаем вектор
![]() +
+
![]() ;
;
 в
в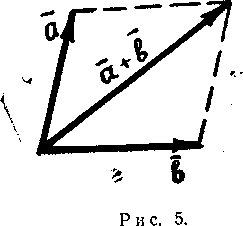 ектор
(
ектор
(![]() +
+
![]() )
складываем с вектором
)
складываем с вектором
![]() и получаем искомый вектор
и получаем искомый вектор
![]() +
+
![]() +
+
![]() (рис. ).
(рис. ).
Из рис. видно, что искомый вектор суммы
трех векторов можно получить, если к
вектору
![]() приложить вектор
приложить вектор
![]() ,
к вектору
,
к вектору
![]() приложить вектор
приложить вектор
![]() и тогда вектор, идущий от начала первого
вектора до конца последнего вектора
будет искомым.
и тогда вектор, идущий от начала первого
вектора до конца последнего вектора
будет искомым.
Это правило, называемое «правилом многоугольника», остается справедливым при нахождении суммы любого конечного числа векторов. При этом сумма не зависит от порядка слагаемых.
Если при сложении нескольких векторов конец последнего вектора совпадает с началом первого вектора, то сумма равна нуль-вектору.
? Какой особенностью отличается многоугольник векторов, сумма которых равна нулю?
В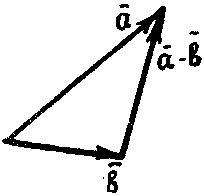 ычитание
векторов
ычитание
векторов
Если даны два вектора
![]() и
и
![]() ,
то разностью
,
то разностью
![]() —
—
![]() называется такой третий вектор
называется такой третий вектор
![]() ,
который в сумме с вектором
,
который в сумме с вектором
![]() составляет вектор
составляет вектор
![]() .
.
Из определения суммы двух векторов
вытекает правило построения вектора
разности: векторы
![]() и
и
![]() приводят к общему началу и тогда
вектор, идущий от конца вектора
приводят к общему началу и тогда
вектор, идущий от конца вектора
![]() к концу вектора
к концу вектора
![]() будет искомым (рис.).
будет искомым (рис.).
Вычесть из вектора
![]() вектор
вектор
![]() означает, что к вектору
означает, что к вектору
![]() надо прибавить вектор —
надо прибавить вектор —
![]() ,
то есть
,
то есть
![]() —
—
![]() =
=
![]() + (—
+ (—![]() ).
).
 На
рис. к вектору
На
рис. к вектору
![]() приложен вектор —
приложен вектор —
![]() и пользуясь правилом треугольника
найдена разность
и пользуясь правилом треугольника
найдена разность
![]() —
—
![]() .
.
Способ замены вычитания сложением удобен тогда, когда требуется построить алгебраическую сумму нескольких векторов.
Умножение вектора на число
П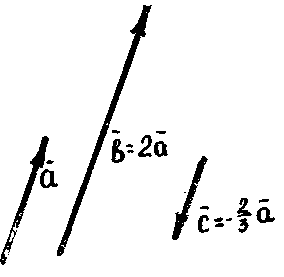 усть
дано вектор
усть
дано вектор
![]() и число р. Произведением вектора
и число р. Произведением вектора
![]() на число р называется новый вектор
на число р называется новый вектор
![]() ,
коллинеарный вектору а, имеющий длину
|
,
коллинеарный вектору а, имеющий длину
|![]() |
= | р ||
|
= | р ||![]() |
и тоже направление, что и вектор
|
и тоже направление, что и вектор
![]() ,
если р>0, и
,
если р>0, и
противоположное направление, если р![]() О,
при этом
О,
при этом
![]() = р
= р![]() = 0, если р = 0 или
= 0, если р = 0 или
![]() = 0
= 0
На рис. вектор
![]() = 2
= 2![]() (число р = 2), а вектор
(число р = 2), а вектор
![]() = -
= -![]()
![]() (число р = -
(число р = -![]() ).
).
Противоположный вектор –![]() можно рассматривать как результат
умножения вектора
можно рассматривать как результат
умножения вектора
![]() на р = -1:
на р = -1:
-![]() = (-1)
= (-1)
![]() .
.
Так, западный ветер можно представить как отрицательный восточный ветер.
Очевидно, что
![]() + (-
+ (-![]() )
= 0.
)
= 0.
Из определения произведения вектора на число следуют свойство этого произведения:
![]() = p
= p![]()
![]() b ||
b ||![]()
