
- •Основные понятия.
- •Процесс оптимизации.
- •G множество допустимых
- •2 Вида задач оптимизации:
- •Методы одномерной оптимизации.
- •2 Варианта:
- •2 Способа:
- •Аналитический способ нахождения локального минимума.
- •Численные методы.
- •Методы одномерного поиска.
- •Метод золотого сечения.
- •Одномерная оптимизация с использованием производных.
- •Методы для нахождения корня уравнения функции 1-ой переменной.
- •Безусловная оптимизация.
- •Функции 2-х переменных
- •Методы прямого поиска.
- •Метод координатного спуска.
- •Градиентные методы. Метод наискорейшего спуска.
- •Анализ метода.
- •Метод Ньютона.
- •1 И 2 не подходят для оптимизации.
- •Задачи оптимизации с ограничениями – разностями (зор)
- •Метод исключения
- •Метод множителей Лагранжа.
- •5 Условий дают систему линейных уравнений Нелинейное программирование (нлп).
- •Задачи линейного программирования (лп).
Московский государственный авиационный институт
![]()
Кафедра прикладной информатики
Лекции
(осенний семестр 2000-2001 уч.гг.)
по дисциплине:
“ОПТИМИЗАЦИЯ В САПР ”
Москва
2001г.
Содержание:
-
Основные понятия
-
понятие САПР
-
процесс оптимизации
Методы одномерной оптимизации
-
аналитический способ
-
численный способ
Методы одномерного поиска
-
метод “золотого сечения”
Одномерная оптимизация с использованием производных
-
метод деление интервала пополам
-
метод Ньютона (метод касательной)
Безусловная опртимизация
Квадратичная аппроксимация (или квадратичное приращение)
Методы прямого поиска
-
приемущества
-
недостатки
Метод координатного спуска
Градиентные методы
-
метод наискорейшего спуска
-
анализ метода
-
метод Ньютона
-
недостатки метода Ньютона
Задачи оптимизации с ограничениями – разностями (ЗОР)
-
метод исключения
-
метод множителей Лагранжа
Нелинейное программирование (НЛП)
-
методы решения НЛП
Задачи линейного программирования (ЛП)
Основные понятия.
САПР – система автоматизированного проектирования. Проектирование сложный процесс, направленный на разработку отдельного объекта.

Способ уменьшения время проектирования – уменьшение числа разработчиков.
Система – совокупность людей, задач и программ, которые взаимосвязаны друг с другом.
Оптимизация – от латинского слова «оптимус» - наилучший – поиск наилучшего, поиск наилучшего проектного изделия.
Процесс оптимизации.
Имеется задача. Для решения задачи нужно формализовать объект и представить его в виде математической модели.
Модели:
-
физические;
-
геометрические (фотография, рисунок);
-
математические.
Математическая модель, та которая
определена с помощью математических
формализмов. Математическая модель не
является точной, а является идеализацией.
Модель характеризуется параметрами,
которые могут быть и числовыми
![]() .
Их часть может характеризовать состояние
объекта – параметры состояния
.
Их часть может характеризовать состояние
объекта – параметры состояния
![]() ,
а другие могут относиться к процессу
проектирования – переменные проектирования
,
а другие могут относиться к процессу
проектирования – переменные проектирования
![]() .
.
Определение параметров состояния - задача моделирования. Определение переменных проектирования – задачи проектирования или задачи оптимизации.
Допустим
имеются 2 переменные
![]() .
Задавая конкретные значения получаем
точку.
.
Задавая конкретные значения получаем
точку.
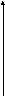
 R – множество
чисел
R – множество
чисел
R
G множество допустимых
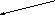 вариантов
вариантов



 p2
допустимое решение
p2
допустимое решение

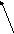

p1
недопустимое решение – не удовлетворяющее наложенным ограничениям
Плоскость множества возможных вариантов, на нее могут быть наложены ограничения.
Отображение
множества
![]() -
целевая функция позволяет формировать
критерий для сравнения различных
решений.
-
целевая функция позволяет формировать
критерий для сравнения различных
решений.
2 Вида задач оптимизации:
-
максимизации;
-
минимизации.
Для оптимизационного решения задачи требуется:
-
Сформулировать задачу;
-
Построить математическую модель (определить множество переменных);
-
Определить ограничения на возможные решения;
-
Определить целевую функцию. Далее применим формальные математические методы, позволяющие найти решения.
Методы одномерной оптимизации.
Постановка: требуется оптимизировать х (формальная постановка)
![]()
![]() -
функция одной переменной
-
функция одной переменной
![]()
![]() - целевая функция.
- целевая функция.
Решение:
найти х, при котором
![]() принимает оптимальное значение.
принимает оптимальное значение.
2 Варианта:
-
минимизировать – задача минимизации;
-
максимизировать – задача максимизации.
Рассмотрим случай минимизации
![]()
![]()
2 Способа:
-
аналитический
-
численный
В аналитическом![]() задается в виде формулы, в численном
задается в виде формулы, в численном
![]() задается в виде черного ящика, на входе
подается х, на выходе значение целевой
функции в этой точке.
задается в виде черного ящика, на входе
подается х, на выходе значение целевой
функции в этой точке.
Пусть функция
определена в некоторой области S
(![]() ),
в случае одномерной оптимизации S
– интервал
),
в случае одномерной оптимизации S
– интервал
![]() :
:
-
точка
 называется глобальным минимумом, если
для
называется глобальным минимумом, если
для
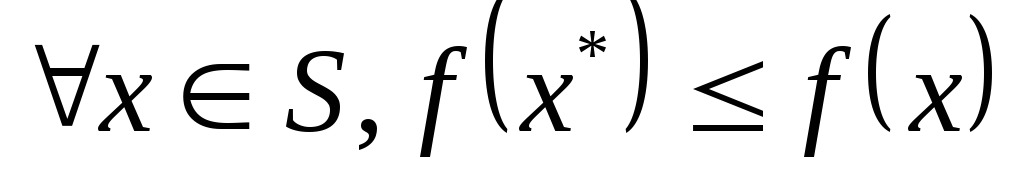
-
точка
 называется строгим глобальным минимумом,
если для
называется строгим глобальным минимумом,
если для
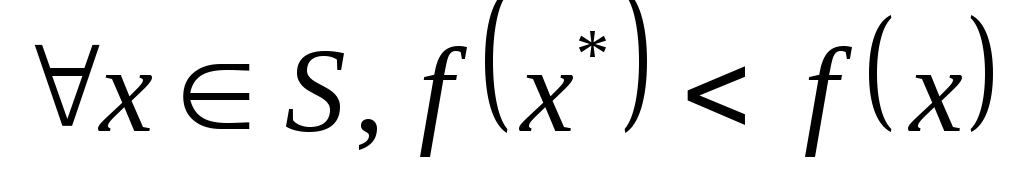
-
точка
 называется локальным минимумом, если
для
называется локальным минимумом, если
для
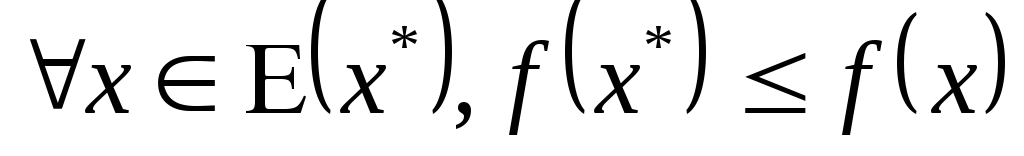
-
точка
 называется строгим локальным минимумом,
если для
называется строгим локальным минимумом,
если для
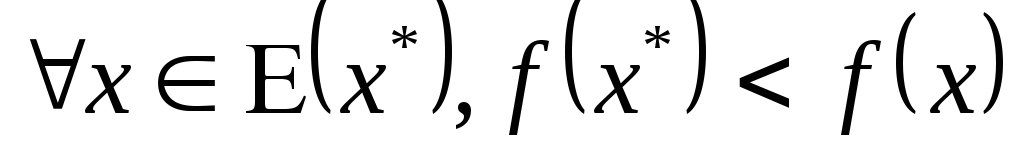
Следствие: любая точка глобального минимума является локальным минимумом, обратное не верно.
