
- •Матрицы и их приложение к исследованию и решению системы линейных алгебраических уравнений Аналитическая геометрия на плоскости и в пространстве.
- •2 Аналитическая геометрия на плоскости
- •Пример 2.
- •Пример 3.
- •3 Векторная алгебра и аналитическая геометрия в пространстве
- •Смешанным произведением трех векторов , и называется число, равное скалярному произведению вектора на вектор , т.Е.:
- •Усл. Печ. Л____ Тираж_____экз. Заказ №______
3 Векторная алгебра и аналитическая геометрия в пространстве
Вектор – отрезок, имеющий определенную длину и направление. Любой вектор можно разложить по ортам координатных осей:
![]() ,
где
,
где
х, у, z –
проекции вектора
![]() на оси координат,
на оси координат,
![]() -
орты (единичные векторы координатных
осей).
-
орты (единичные векторы координатных
осей).
Модуль (длина)
вектора
![]() определяется
по формуле:
определяется
по формуле:
![]() (3.1.1)
(3.1.1)
Если известны координаты
начала
![]() и конца В(
и конца В(![]() )вектора,
то вектор
)вектора,
то вектор
![]() можно записать следующим образом:
можно записать следующим образом:
![]() (3.1.2)
(3.1.2)
Скалярным
произведением двух ненулевых векторов
![]() и
и
![]() называется произведение их модулей на
косинус угла между ними:
называется произведение их модулей на
косинус угла между ними:
![]() .
.
Отсюда нетрудно определить угол между векторами
![]() . (3.1.3)
. (3.1.3)
Если
векторы
![]() и
и
![]() заданы своими проекциями
заданы своими проекциями
![]() =
=![]() и
и
![]() =
=![]() ,
то скалярное
произведение
находится по формуле:
,
то скалярное
произведение
находится по формуле:
![]() . (3.1.4)
. (3.1.4)
Векторы ортогональны, если их скалярное произведение равно нулю, т.е.:
![]() . (3.1.5)
. (3.1.5)
Векторным
произведением
двух векторов называется вектор
![]() ,
определяемый условиями:
,
определяемый условиями:
-
вектор
 перпендикулярен векторам
перпендикулярен векторам
 и
и
 ,
т.е.
,
т.е.

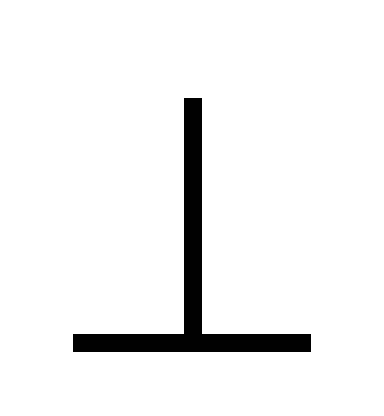
 ,
,


 ;
; -
векторы
 ,
, и
и
 образуют
правую тройку;
образуют
правую тройку; -
длина вектора
 равна площади параллелограмма,
построенного на векторах
равна площади параллелограмма,
построенного на векторах
 и
и
 как на сторонах, т.е.
как на сторонах, т.е.
![]() .
.
Для
векторов, заданных проекциями
![]() =
=![]() и
и
![]() =
=![]() ,
векторное произведение имеет вид:
,
векторное произведение имеет вид:
 . (3.1.6)
. (3.1.6)
Отсюда, условие коллинеарности векторов:
![]() . (3.1.7)
. (3.1.7)
Смешанным произведением трех векторов , и называется число, равное скалярному произведению вектора на вектор , т.Е.:
(![]() )
)![]() .
.
Геометрически
модуль смешанного произведения равен
объему параллелепипеда, построенного
на векторах
![]() ,
,![]() и
и
![]() ,
как на ребрах.
,
как на ребрах.
Если векторы заданы
проекциями
![]() =
=![]() ,
,
![]() =
=![]() и
и
![]() =
=![]() ,
то смешанное произведение имеет вид:
,
то смешанное произведение имеет вид:
 . (3.1.8)
. (3.1.8)
Условие компланарности (принадлежности трех векторов одной плоскости или параллельности плоскостям), имеет вид:
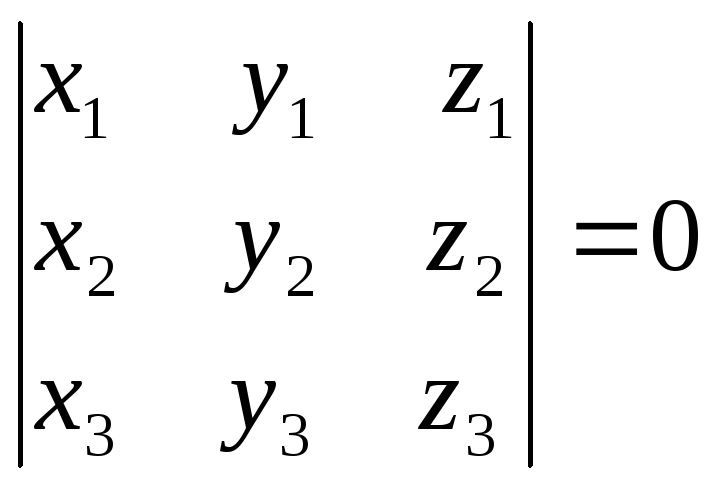 . (3.1.9)
. (3.1.9)
Знание векторной алгебры во многом упрощает решение задач по аналитической геометрии в пространстве.
Так,
уравнение плоскости, проходящей через
заданную точку М(![]() ),
перпендикулярно вектору
),
перпендикулярно вектору
![]() имеет вид:
имеет вид:
![]() . (3.1.10)
. (3.1.10)
Уравнение
плоскости, проходящей через три точки:
А(![]() ),
В(
),
В(![]() ),
и С(
),
и С(![]() ),
имеет вид:
),
имеет вид:
 (3.1.11)
(3.1.11)
Канонические уравнения прямой в пространстве имеют вид:
![]() , (3.1.12)
, (3.1.12)
где (![]() )-точка,
через которую проходит прямая;
)-точка,
через которую проходит прямая;
![]() -проекции
направляющего вектора прямой.
-проекции
направляющего вектора прямой.
Уравнения прямой, проходящей через две точки, определяются так:
![]() . (3.1.13)
. (3.1.13)
Если
прямая вида (3.1.12) перпендикулярна
плоскости, заданной общим уравнением:
![]() ,
то выполняется условие:
,
то выполняется условие:
![]() . (3.1.14)
. (3.1.14)
Рассмотрим несколько примеров применения изложенных выше теоретических положений.
Пример 6.
Записать
вектор
![]() в системе орт и найти его модуль, если
А(1, 2, 3);
в системе орт и найти его модуль, если
А(1, 2, 3);
В(0, 1, 5).
Решение.
Используя формулу (3.1.2) получим:
![]() =(0-1)
=(0-1)![]() =
=![]() .
.
Используя формулу (3.1.1), найдем модуль этого вектора:
![]() (ед.дл.)
(ед.дл.)
Пример 7.
Найти
угол между векторами
![]() и
и
![]() .
.
Решение.
Используя формулу (3.1.3), получим:
![]() ,
,
что соответствует
углу
![]() .
.
Пример 8.
Найти
площадь треугольника, образованного
двумя векторами
![]() и
и
![]() ,
выходящими из одной точки.
,
выходящими из одной точки.
Решение.
Площадь
треугольника, построенного на векторах
![]() и
и
![]() ,
равна половине площади параллелограмма,
построенного на этих же векторах как
на сторонах, т.е. равна
,
равна половине площади параллелограмма,
построенного на этих же векторах как
на сторонах, т.е. равна
![]() модуля векторного произведения векторов
модуля векторного произведения векторов
![]() и
и
![]() :
:
![]() .
.
Векторное произведение найдем по формуле (3.1.6):

Найдем модуль полученного вектора, используя формулу (3.1.1):
![]()
Тогда искомая площадь будет:
![]() (кв.ед.)
(кв.ед.)
Пример 9.
Найти объем пирамиды, построенной на трех некомпланарных векторах:
![]() .
.
Решение:
Объем пирамиды, построенной на трех некомпланарных векторах как на ребрах, равен
![]() ,
где
,
где
![]() ,
,
где
![]() -смешанное
произведение векторов.
-смешанное
произведение векторов.
Величину
![]() найдем по формуле (3.1.8):
найдем по формуле (3.1.8):
![]() =
=
Тогда
![]() (куб.ед.).
(куб.ед.).
Пример 10.
Найти каноническое уравнение прямой, проходящей через две точки А(1,2,5) и В(0,1,2).
Решение:
Подставив координаты точек А и В в уравнение (3.1.13), получим:
![]() ;
;
![]() ;
;
![]() .
.
Пример 11.
Найти уравнение плоскости, проходящей через три точки: А(1, 2, 3);
В(1, 1, 0) и С(2, 3, 1).
Решение:
Используя уравнение (3.1.11), получим:


(х-1) ,
,
![]()
![]()
![]()
Пример 12.
Через
точку А(1, 0, 2) провести прямую,
перпендикулярную плоскости
![]()
Решение.
Используем канонические уравнения прямой (3.1.12), подставив координаты точки А, получим:
![]() .
.
Проекции
направляющего вектора прямой
![]() найдем из условия перпендикулярности
прямой и плоскости (3.1.14).
найдем из условия перпендикулярности
прямой и плоскости (3.1.14).
В нашем
случае это будет:![]() ,
тогда будем иметь:
,
тогда будем иметь:![]() .
.
Задание 1. Найдите
матрицу
![]() ,
если:
,
если:
1)
 ;
2)
;
2)
 ;
;
3) ;
4)
;
4)
 ;
;
5)
 ;
6)
;
6)
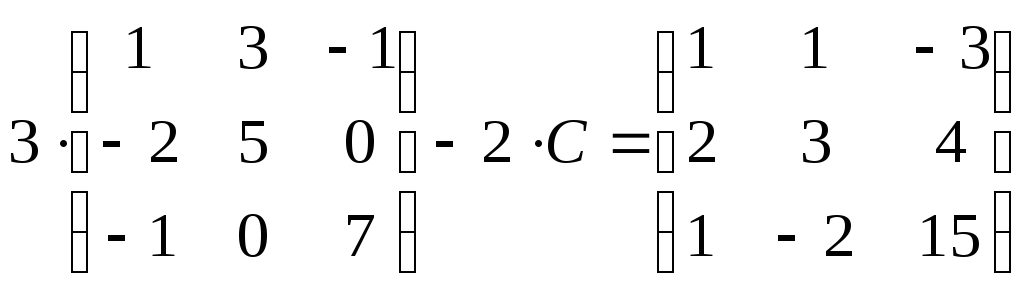 ;
;
7)
 ;
8)
;
8)
 ;
;
9)
 ;
;
10)
 ;
;
11) ;
;
12)
 ;
;
13)
 ;
;
14)
 ;
;
15)
 ;
;
16)
 ;
;
17)
 ;
;
18)
 ;
;
19)
 ;
;
20)
 ;
;
21)
 ;
;
22)
 ;
;
23)
 ;
;
24)
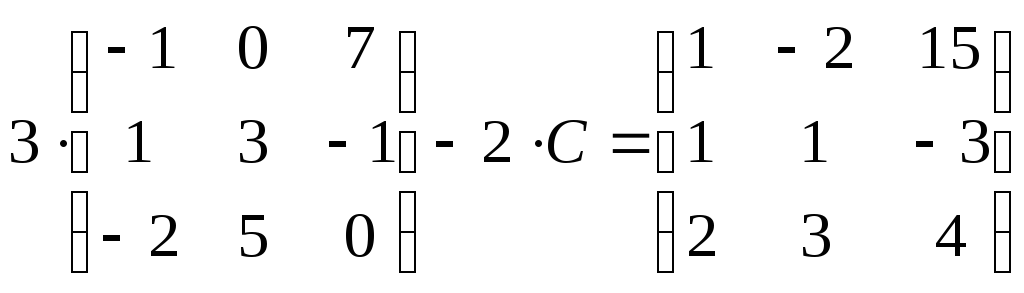 ;
;
25)
 ;
;
26)
 ;
;
27)
 ;
;
28)
 ;
;
29)
 ;
;
30)
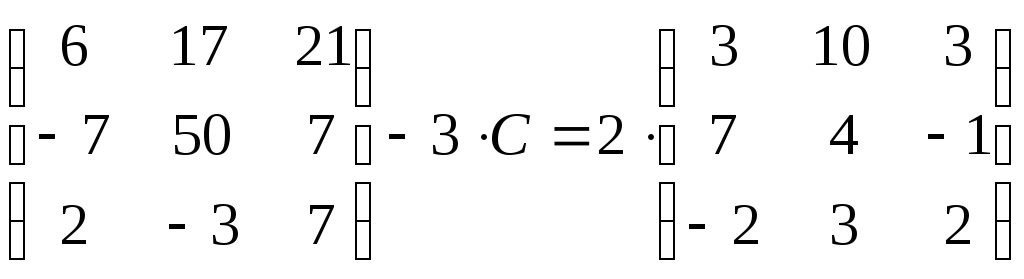 .
.
Задание 2. Решите матричные уравнения и проверьте подстановкой:
1 a)
![]() ;
б)
;
б)
 ;
;
2 а)
![]() ;
б)
;
б)
 ;
;
3 а)
![]() ;
б)
;
б)
 ;
;
4 a)
![]() ;
б)
;
б)
 ;
;
5 а)
![]() ;
б)
;
б)
 ;
;
6 а)
![]() ;
б)
;
б)
 ;
;
7 a)
![]() ;
б)
;
б)
 ;
;
8 а)
![]() ;
б)
;
б)
 ;
;
9 а)
![]() ;
б)
;
б)
 ;
;
10 а)
![]() ;
б)
;
б)
 ;
;
11 а)
![]() ;
б)
;
б)
 ;
;
12 а)
![]() ;
б)
;
б)
 ;
;
13 а)
![]() ;
б)
;
б)
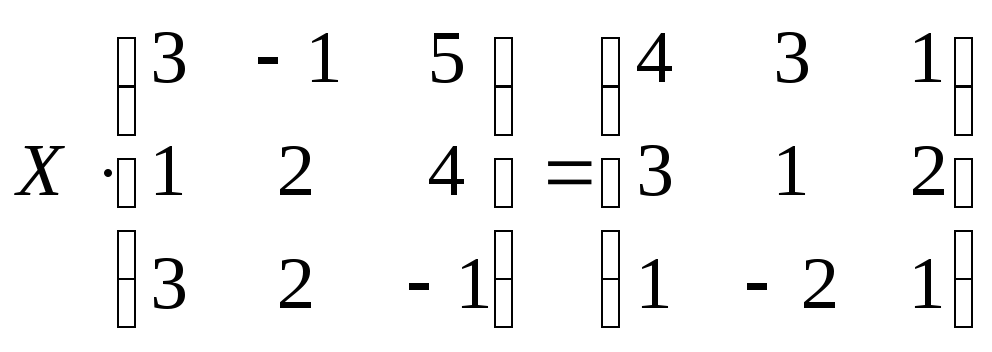 ;
;
14 а)
![]() ;
б)
;
б)
 ;
;
15 а)
![]() ;
б)
;
б)
 ;
;
16 а)
![]() ;
б)
;
б)
 ;
;
17 а)
![]() ;
б)
;
б)
 ;
;
18 а)
![]() ;
б )
;
б )
 ;
;
19 а)
![]() ;
б)
;
б)
 ;
;
20 а)
![]() ;
б )
;
б )
 ;
;
21 а)
![]() ;
б)
;
б)
 ;
;
22 а)
![]() ;
б)
;
б)
 ;
;
23 а)
![]() ;
б)
;
б)
 ;
;
24 а)
![]() ;
б)
;
б)
 ;
;
25 а)
![]() ;
б)
;
б)
 ;
;
26 а)
![]() ;
б)
;
б)
 ;
;
27 а)
![]() ;
б)
;
б)
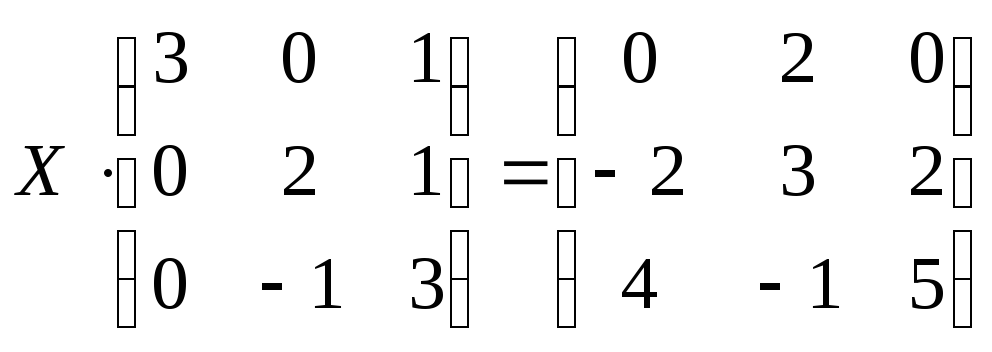 ;
;
28 а)
![]() ;
б)
;
б)
 ;
;
29 а)
![]() ;
б)
;
б)
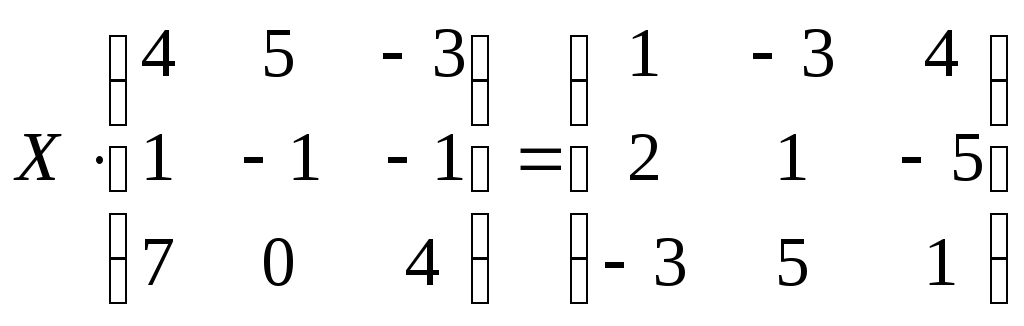 ;
;
30 а)
![]() ;
б)
;
б)
 .
.
Задание 3. Решите систему уравнений с помощью обратной матрицы:
1
 2
2

3
 4
4

5
 6
6

7
 8
8

9
 10
10

11
 12
12

13
 14
14

15
 16
16

17
 18
18

19
 20
20

21
 22
22
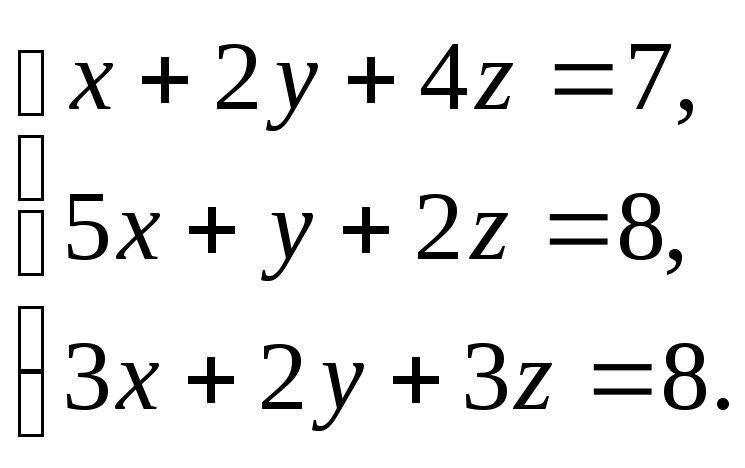
23
 24
24

25
 26
26

27
 28
28

29
 30
30
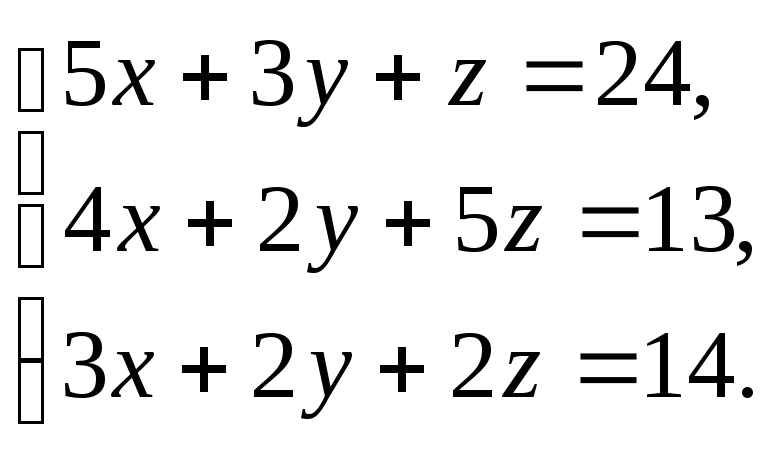
Задание 4. Исследуйте следующие системы уравнений и найдите их решения:
1 а)
 б)
б)
 ъ
ъ
2 а)
 б)
б)

3 а)
 б)
б)

4 а)
 б)
б)

5 а)
 б)
б)

6 а)
 б)
б)

7 а)
 б)
б)
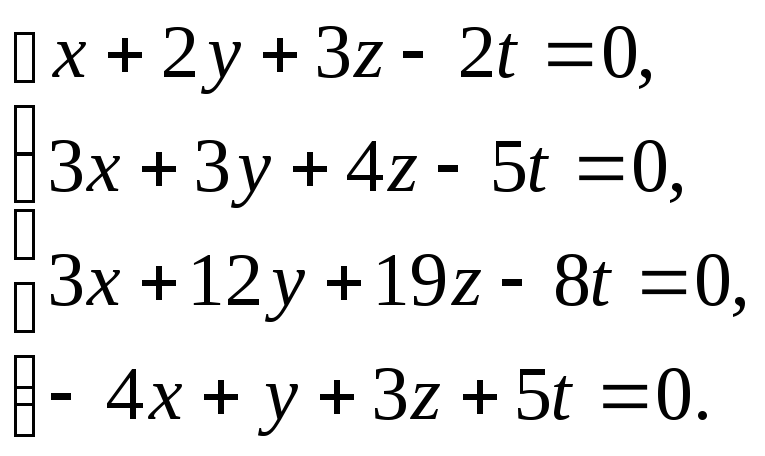
8 а)
 б)
б)

9 а)
 б)
б)

10 а)
 б)
б)

11 а)
 б)
б)

12 а)
 б)
б)

13 а)
 б)
б)

14 а)
 б)
б)

15 а)
 б)
б)
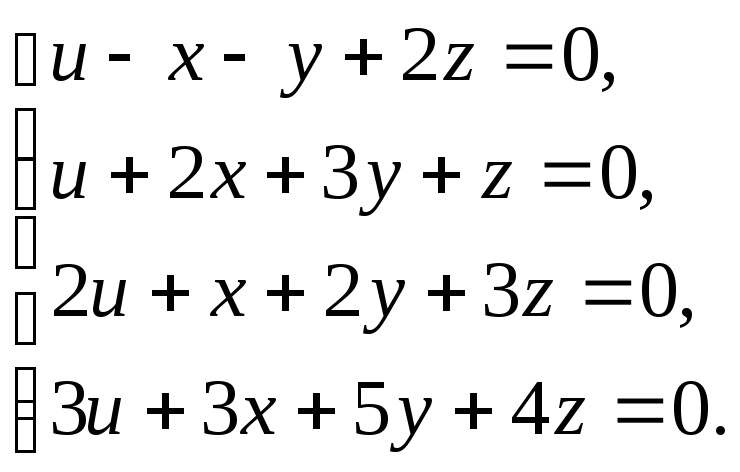
16 а)
 б)
б)
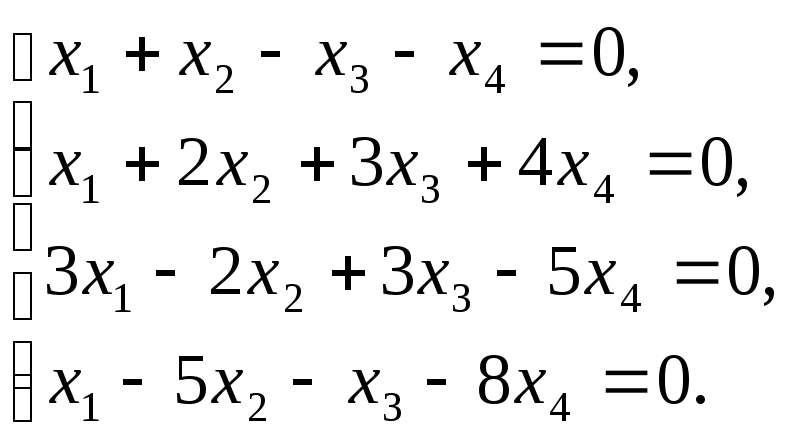
17 а)
 б)
б)
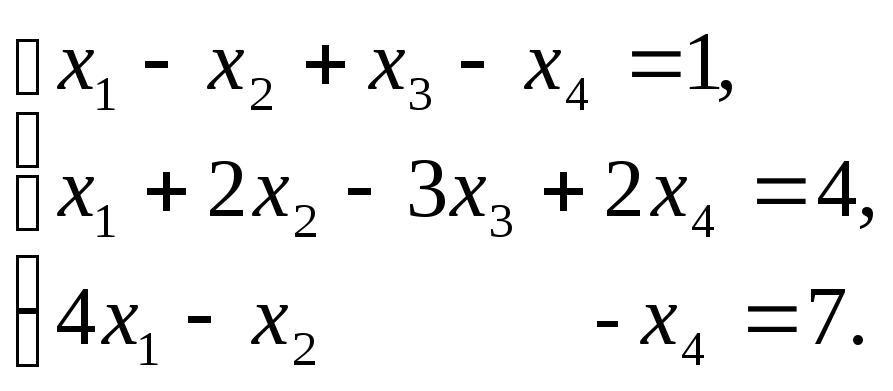
18 а)
 б)
б)

19 а)
 б)
б)

20 а)
 б)
б)

21 а)
 б)
б)

22 а)
 б)
б)

23 а)
 б)
б)

24 а)
 б)
б)

25 а)
 б)
б)

26 а)
 б)
б)

27 а)
 б)
б)

28 а)
 б)
б)

29 а)
 б)
б)

30 а)
 б)
б)

Задача 5
Даны
координаты вершин треугольника
![]() .
.
Найти:
1) длину
стороны
![]() ;
;
2)
уравнение стороны
![]() и ее угловой коэффициент;
и ее угловой коэффициент;
3)
уравнение и длину высоты
![]() ;
;
4)
уравнение медианы
![]() ;
;
5)
уравнение биссектрисы
![]() ;
;
6)
координаты точки
![]() ,
симметричной точке
,
симметричной точке
![]() относительно
прямой
относительно
прямой
![]() .
.
-
А(-5;0), В(7;9), С(5;-5). 11. А(-5;2), В(7;-7), С(5;7).
-
А(-7;2),В(5;11),С(3;-3). 12. А(-7;5), В(5;-4), С(3;10).
-
А(-5;-3), В(7;6), С(5;-8). 13. А(-7;1), В(5;-8), С(3;10).
-
А(-6;-2), В(6;7), С(4;-7). 14. А(0;3), В(12;-6), С(10;8).
-
А(-8;-4), В(4;5), С(2;-9). 15. А(-8;4), В(4;-5), С(2;9).
-
А(0;-1), В(12;8), С(10;-6). 16. А(-2;2), В(10;-7), С(8;7).
-
А(-6;1), В(6;10), С(4;-4). 17. А(1;2), В(13;-7), С(11;7).
-
А(-2;-4), В(10;5), С(8;-9). 18. А(-4;1), В(8;-8), С(6;6).
-
А(-3;0), В(9;9), С(7;-5). 19. А(-7;-1), В(5;-10), С(3;4).
-
А(-9;-2), В(3;7), С(1;-7). 20. А(-3;3), В(9;-6), С(7;8).
Задача 6
Даны
координаты вершин пирамиды
![]() .
.
Найти:
-
векторы
 в
системе орт и их модули;
в
системе орт и их модули; -
угол между векторами
 ;
; -
площадь грани
 ;
; -
объем пирамиды
 ;
; -
уравнение ребра
 ;
; -
уравнение плоскости
 ;
; -
уравнение высоты, опущенной из точки
 на плоскость
на плоскость
 ;
; -
Координаты точки
 ,
симметричной точке
,
симметричной точке
 ,
относительно прямой
,
относительно прямой
 ;
; -
Координаты проекции точки
 на плоскость
на плоскость
 ;
; -
Уравнение плоскости, проходящей через сторону
 параллельно стороне
параллельно стороне
 ;
; -
Расстояние от точки
 до прямой
до прямой
 ;
; -
Расстояние между прямыми
 и
и
 .
.
-
А(1;2;1), В(-1;5;1), С(-1;2;7), D(1;5;9).
-
А(2;3;2), В(0;6;2), С(0;3;8), D(2;6;10).
-
А(0;3;2), В(-2;6;2), С(-2;3;8), D(0;6;10).
-
А(2;1;2), В(0;4;2), С(0;1;8), D(2;4;10).
-
А(2;3;0), В(0;6;0), С(0;3;6), D(2;6;8).
-
А(2;2;1), В(0;5;1), С(0;2;7), D(2;5;9).
-
А(1;3;1), В(-1;6;1), С(-1;3;7), D(1;6;9).
-
А(1;2;2), В(-1;5;2), С(-1;2;8), D(1;5;10).
-
А(2;3;1), В(0;6;1), С(0;3;7), D(2;6;9).
-
А(2;2;2), В(0;5;2), С(0;2;8), D(2;5;10).
-
А(1;3;2), В(-1;6;2), С(-1;3;8), D(1;6;10).
-
А(0;1;2), В(-2;4;2), С(-2;1;8), D(0;4;10).
-
А(0;3;0), В(-2;6;0), С(-2;3;6), D(0;6;8).
-
А(2;1;0), В(0;4;0), С(0;1;6), D(2;4;8).
-
А(0;2;1), В(-2;5;1), С(-2;2;7), D(0;5;9).
-
А(1;1;1), В(-1;4;1), С(-1;1;7), D(1;4;9).
-
А(1;2;0), В(-1;5;0), С(-1;2;6), D(1;5;8).
-
А(0;1;0), В(-2;4;0), С(-2;1;6), D(0;4;8).
-
А(0;1;1), В(-2;4;1), С(-2;1;7), D(0;5;9).
-
А(0;2;0), В(-2;5;0), С(-2;2;6), D(0;5;8).
Литература:
1. Письменный Д.Т. Конспект лекций по высшей математике. –М.: Рольф, 2002.-288с., с ил.
2. Лунгу К.Н., Письменный Д.Т., Федин С.Н., Шевченко Ю.А. Сборник задач по высшей математике. 1 курс. –М.: Рольф, 2001.-576с., с ил.
Лицензия РБ на издательскую деятельность №0261 от 10 апреля 1998 года.
Подписано в печать _____2008г. Формат 60х84.
Бумага типографская. Гарнитура Таймс.
