
- •Матрицы и их приложение к исследованию и решению системы линейных алгебраических уравнений Аналитическая геометрия на плоскости и в пространстве.
- •2 Аналитическая геометрия на плоскости
- •Пример 2.
- •Пример 3.
- •3 Векторная алгебра и аналитическая геометрия в пространстве
- •Смешанным произведением трех векторов , и называется число, равное скалярному произведению вектора на вектор , т.Е.:
- •Усл. Печ. Л____ Тираж_____экз. Заказ №______
Министерство сельского хозяйства Российской Федерации
Федеральное государственное образовательное учреждение высшего профессионального образования
«Башкирский государственный аграрный университет»
Кафедра математики
Матрицы и их приложение к исследованию и решению системы линейных алгебраических уравнений Аналитическая геометрия на плоскости и в пространстве.
Методические указания
к выполнению расчетно- графической работы №1
по дисциплине «Математика»
Направление 110800 Агроинженерия
Уфа – 2008
УДК 378.147:51
ББК 74.58:22.1
М34
Рекомендовано к изданию методической комиссией факультета механизации сельского хозяйства (протокол №14 от 6 декабря 2002 года) и заседанием кафедры математики (протокол №5 от 28 декабря 2002 года)
Составители:
доцент Пономарева Л.А.
ст. преподаватель Карамов В.И.
Рецензент: доцент кафедры физики Юмагужин Р.Ю.
Ответственный за выпуск: зав. кафедрой математики
доцент Лукманов Р.Л.
Предварительно приведем вопросы по разделу, на которые следует ответить перед решением задач и на зачете.
1. Основные понятия, связанные с матрицами (матрица-строка, матрица-столбец, определитель квадратной матрицы и т.п.)
2. Сложение матриц и умножение матрицы на число. Свойства этих действий.
3. Умножение матриц и его свойства.
4. Обратная матрица, ее строение.
5. Матричная запись системы линейных алгебраических уравнений, решение ее с помощью обратной матрицы.
6. Решение матричных уравнений с помощью обратной матрицы.
7. Исследование системы уравнений первой степени общего вида; основная и расширенная матрицы; ранг матрицы; теорема Кронекера-Капелли.
Далее рассмотрим образец решения некоторых типовых задач.
Задача 1. Исследовать систему линейных уравнений; если она совместна, то найти ее общее и одно частное решение.

Решение. Приведем расширенную матрицу системы к ступенчатому виду:
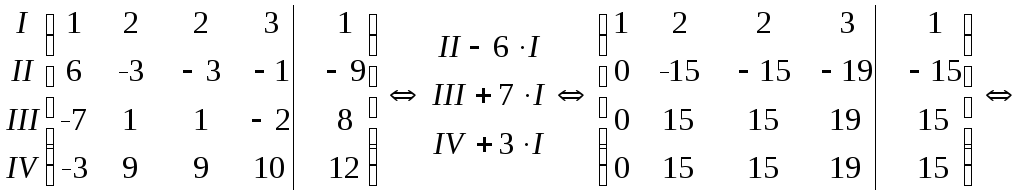

Так как
![]() ,
то система совместна и неопределена.
,
то система совместна и неопределена.
Количество главных
переменных равно
![]() ,
количество свободных переменных равно
,
количество свободных переменных равно
![]() .
.
Выберем какой-нибудь
отличный от нуля минор второго порядка
полученной матрицы
![]() ,
например, минор
,
например, минор
![]() .
Его столбцы – первый и второй столбцы
матрицы
.
Его столбцы – первый и второй столбцы
матрицы
![]() - соответствуют переменным
- соответствуют переменным
![]() и
и
![]() - это будут главные
переменные, а
- это будут главные
переменные, а
![]() и
и
![]() - свободные переменные.
- свободные переменные.
Заметим, что в
качестве главных переменных в данном
примере нельзя выбрать пару
![]() и
и
![]() ,
т.к. любой соответствующий им минор
равен нулю:
,
т.к. любой соответствующий им минор
равен нулю:
![]() ,
,
![]() ,
,
![]() .
.
Запишем систему уравнений, соответствующую полученной расширенной матрице:

Перепишем ее в виде:
 или
или

Обозначим свободные
переменные:
![]() через
через
![]() ,
,
![]() через
через
![]() .
Запишем общее решение системы:
.
Запишем общее решение системы:
![]() ;
частное решение
;
частное решение
![]() .
.
Задача 2. Исследовать систему линейных уравнений:

Решение. Приведем к ступенчатому виду расширенную матрицу системы:

Так
как
![]() ,
то система несовместна (не имеет решений).
В самом деле, последней строке полученной
расширенной матрицы соответствует
уравнение
,
то система несовместна (не имеет решений).
В самом деле, последней строке полученной
расширенной матрицы соответствует
уравнение
![]() ,
не имеющее решений.
,
не имеющее решений.
Ответ: система несовместна.
Задача 3. Найти общее решение и фундаментальную систему решений однородной системы линейных уравнений:
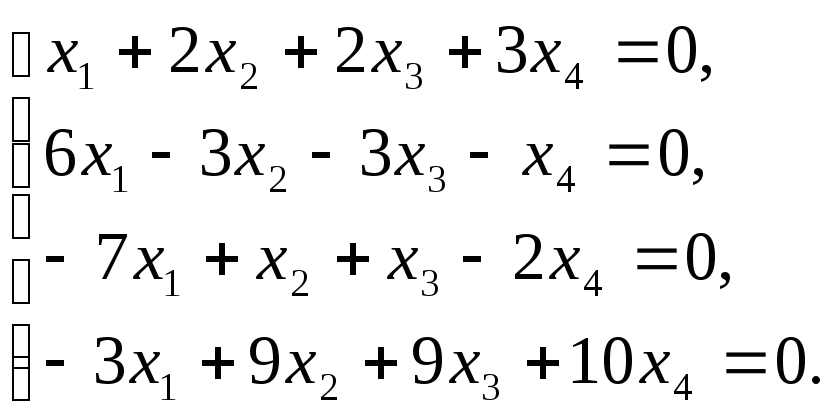
Решение. Приведем матрицу системы к ступенчатому виду:

Так как
![]() ,
то система неопределенна. В качестве
главных переменных можно выбрать
,
то система неопределенна. В качестве
главных переменных можно выбрать
![]() и
и
![]() ,
соответствующие столбцам ненулевого
минора второго порядка:
,
соответствующие столбцам ненулевого
минора второго порядка:
![]() ;
в качестве свободных переменных -
;
в качестве свободных переменных -
![]() и
и
![]() .
.
Запишем систему, соответствующую полученной матрице:

Из второго уравнения
получим
![]() .
Подставляя это
выражение в первое уравнение, получим
.
Подставляя это
выражение в первое уравнение, получим
![]() .
.
Обозначая свободные
переменные:
![]() через
через
![]() ,
,
![]() через
через
![]() ,
запишем общее решение системы:
,
запишем общее решение системы:
![]() .
.
Фундаментальную
систему решений образует, например,
пара решений
![]() и
и
![]() .
.
Ответ: общее решение
системы
![]() ;
;
фундаментальная
система решений
![]() .
.
