БАЛАКОВСКИЙ ИНСТИТУТ ТЕХНИКИ, ТЕХНОЛОГИИ И УПРАВЛЕНИЯ

ФАКУЛЬТЕТ ИНЖИНЕРО – СТРОИТЕЛЬНЫЙ

КАФЕДРА УПРАВЛЕНИЯ И ИНФОРМАТИКИ В ТЕХНИЧЕСКИХ СИСТЕМАХ

КУРСОВАЯ РАБОТА

по дисциплине ТАУ

 Исследование устойчивости линейных и нелинейных систем

автоматического управления

Выполнили ст. гр. УИТ-41в

Петрова Е.В.

Принял доцент каф. УИТ

Скоробогатова Т.Н._______

«___»_______________2004г

2004

Вариант 25

Цель работы: освоение математических методов теории систем. Приобретение практических навыков анализа систем управления с применением современных программных и технических средств.

Исходная схема.

Дано:

, , , ,

,

Задание:

Часть 1: Линейная система.

1. Упростить систему.

2. Посчитать устойчивость (любым способом).

3. Построить переходную характеристику.

4. Построить амплитудно-частотную характеристику.

5. Построить ЛАЧХ и ЛФЧХ.

Часть 2: Нелинейная система.

Часть 3: Дискретная система.

1. Z – преобразование.

2. - преобразование.

3. - преобразование.

4. Посчитать устойчивость.

5. Построить ЛАЧХ и ЛФЧХ.

Часть 4: Вывод.

Решение:

Часть 1: Линейная система.

1.1 Преобразуем структурную схему.

Звенья соединены последовательно, следовательно, имеем:

В соответствии с данным преобразованием, структурная схема САУ примет вид:

Звенья W₆(p), W₇(p) включены встречно – параллельно (сумматор положительный), следовательно:

тогда:

Исходя из схемы, по правилу преобразования структурных схем, получим передаточную функцию системы:

,

Получили передаточную функцию данной системы:

2. Посчитаем устойчивость системы.

Для того чтобы проверить устойчивость системы, воспользуемся теоремой Ляпунова и критерием Михайлова.

Теорема: автоматическая система, описанная линейным дифференциальным уравнением с постоянными коэффициентами, будет устойчива, если вещественные корни дифференциального уравнения будут отрицательны, а комплексные корни будут иметь отрицательную реальную часть.

Найдем корни характеристического уравнения данной системы.

Данная система неустойчива, так как характеристическое уравнение имеет положительный корень.

Критерий: для устойчивой системы необходимо и достаточно, чтобы годограф Михайлова при изменении частоты от нуля до бесконечности повернулся против часовой стрелки, начиная с вещественной оси, на число квадрантов равное порядку характеристического уравнения, последовательно проходя эти квадранты.

Запишем передаточную функцию в следующем виде:

Умножим и числитель, и знаменатель на комплексно сопряженное число.

После всех преобразований получим:

Ведем замену

Выделим мнимую и реальную части:

Построим годограф:

Мы видим, что система не устойчива, т.к. не выполняется условие последовательного прохождения квадрантов.

Устойчивость по Гурвицу: для устойчивости системы необходимо и достаточно, чтобы все миноры определителя Гурвица были положительны.

Запишем характеристическое уравнение для рассматриваемой системы, получим:

.

Составим определители Гурвица из коэффициентов характеристического уравнения:;;;.

=

=

=.

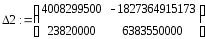
Согласно критерию Гурвица, система не устойчива, т.к. один из миноров имеет отрицательный знак.

2. Построим переходный процесс.

На вход подается -функция Хевисайда.

Функция, определяющая изменение выходной величины системы при подаче на ее вход единичного ступенчатого воздействия и при нулевых начальных условиях называется переходной функцией системы и обозначается: h(t).

Найдем переходную функцию с помощью преобразований Лапласа.

Найдем корни характеристического уравнения данной системы.

Рассчитаем компоненты переходной функции для каждого из корней характеристического уравнения.

По виду переходной характеристики можно также сказать, что данная система не устойчива.

По переходному процессу определим прямые оценки качества.

а) Время переходного процесса – это время за которое регулируемая величина входит в пятипроцентную трубку.

б) Время первого согласования – это время за которое регулируемая величина первый раз достигает установившееся значение.

в) Перерегулирование – определяем максимальную динамическую ошибку.

г) Время нарастания регулируемой величины – это время за которое регулируемая величина достигает максимальное значение.

д) Число колебаний – определяется числом колебаний регулируемой величины за время регулирования процесса.

Так как система неустойчива, то прямые оценки качества системы не определяются.

2. Построим график амплитудно-частотной характеристики.

Последовательность нахождения частотных характеристик:

1. Сделать замену в передаточной функции .

2. Освободится от мнимых чисел в знаменателе путем умножения числителя и знаменателя выражения на комплексно-сопряженное знаменателю число.

3. Раскрыть скобки и привести подобные члены и разделить в числителе на сумму вещественного и мнимого полиномов.

4. Записать выражения для вещественной и мнимой частотных характеристик.

5. Записать выражения для амплитудно-частотной характеристики.

6. Построить графики.

Построение частотных характеристик по полученной передаточной функции.

Найдем корни характеристического уравнения данной системы.

Запишем передаточную функцию в следующем виде:

Умножим и числитель, и знаменатель на комплексно сопряженное число.

После всех преобразований получим:

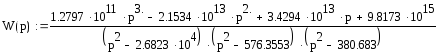
Ведем замену

Выделим мнимую и реальную части:

Построим график АЧХ.

Найдем косвенные оценки качества.

а) Колебательность

, тогда

б) Резонансная частота – это часто при которой амплитуда максимальна.

в) Частота среза – это частота при которой амплитуда равна 1.

г) Полоса пропускания частот – это наилучшее провождение сигнала через систему или коридор ограниченный прямой параллельной оси с координатой . Из точек пересечения данной прямой с АЧХ опускаем перпендикуляры на ось , которые и ограничивают полосу пропускания частот.

В нашем случае его нет.

2. Построим ЛАЧХ и ЛФЧХ.

Для построения ЛАЧХ и ЛФЧХ разомкнем систему, то получим

,

тогда

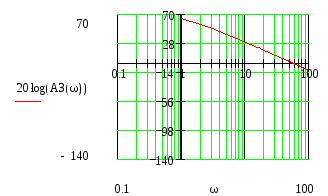
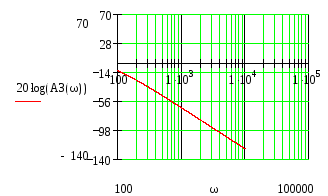
Запас по амплитуде равен , а по фазе .

Часть 2: Нелинейная система.

Дана структурная схема нелинейной САУ:

Нелинейный элемент имеет вид:

Б

А

Предположим, что система работает только на участке АБ, тогда для расчета линеаризуем нелинейный элемент для этого найдем коэффициент усиления

Согласно полученному выражению можем преобразовать структурную схему.

Звенья соединены последовательно, следовательно, имеем:

В соответствии с данным преобразованием, структурная схема САУ примет вид:

Звенья W₆(p), W₇(p) включены встречно – параллельно (сумматор положительный), следовательно:

тогда:

Исходя из схемы, по правилу преобразования структурных схем, получим передаточную функцию системы:

,

Получили передаточную функцию данной системы: