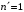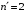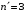- •«Физические основы электронной техники. Квантовая механика»
- •2. Движение микрочастицы в поле центральной
- •2.1. Поле центральной симметрии
- •2. 2. Атом водорода. Радиальная часть волновой функции
- •2.3. Схема уровней энергии и спектр атома водорода
- •2.4. Волновые функции атома водорода и распределение электронной плотности
- •2.5. Изотопический сдвиг и водородоподобные ионы
- •2.6. Энергетический спектр атомов щелочных металлов
2.5. Изотопический сдвиг и водородоподобные ионы
Кроме
легкого изотопа водорода
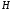 существуют
еще два тяжелых изотопа: дейтерий
существуют
еще два тяжелых изотопа: дейтерий
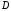 и тритий
и тритий
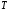 .
Ядро дейтерия, кроме протона, имеет еще
один нейтрон, а ядро трития – два
нейтрона. Спектры тяжелых изотопов
водорода подчиняются той же формуле
(2.70), но постоянная Ридберга для них
будет другой. Расчет по формуле дает:
.
Ядро дейтерия, кроме протона, имеет еще
один нейтрон, а ядро трития – два
нейтрона. Спектры тяжелых изотопов
водорода подчиняются той же формуле
(2.70), но постоянная Ридберга для них
будет другой. Расчет по формуле дает:
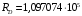 см
–
1,
см
–
1,
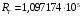 см –
1.
см –
1.
Различие
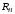 ,
,
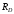 ,
,
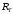 приводит к различию длин волн одних и
тех же линий в спектрах различных
изотопов водорода. Различие в длинах
волн называют изотопическим
сдвигом.
В табл. 2.2 для сравнения приведены длины
волн первых трех линий серии Бальмера
(
приводит к различию длин волн одних и
тех же линий в спектрах различных
изотопов водорода. Различие в длинах
волн называют изотопическим
сдвигом.
В табл. 2.2 для сравнения приведены длины
волн первых трех линий серии Бальмера
( ).
).
Таблица 2.2
|
Линия |
|
|
|
|
|
656.469 |
656.291 |
0.178 |
|
|
486.237 |
486.141 |
0.096 |
|
|
434.173 |
434.055 |
0.118 |
Изотопический сдвиг в спектрах водорода и дейтерия настолько значителен, что четко определяется с помощью обычных спектральных приборов.
Рассмотрим спектр водородоподобных ионов. Приведем спектральную формулу (2.75) для однократно ионизированного атома гелия:
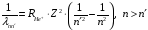 ,
(2.89)
,
(2.89)
где
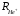 определяется следующим образом
определяется следующим образом
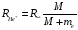 ,
,
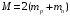 – масса ядра гелия.
– масса ядра гелия.
После
вычислений получим
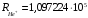 см
–
1.
см
–
1.
Для
однократно ионизированного атома гелия
первые члены серий аналогичных сериям
Лаймана и Бальмера для водорода (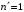 и
и
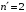 )
лежат в ультрафиолетовой области (см.
табл.2.3).
)
лежат в ультрафиолетовой области (см.
табл.2.3).
Таблица 2.3
|
Длина
волны |
||
|
|
|
|
|
30.379 |
164.050 |
468.715 |
|
25.632 |
121.518 |
320.410 |
|
24.303 |
108.498 |
273.417 |
Аналогично
определяются спектры ионов
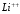 ,
,
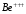 и
др.
и
др.
Рассмотрим
еще одну интересную систему – позитроний,
которая состоит из двух частиц: позитрона
и электрона. «Атомы» позитрония являются
метастабильными и через короткий отрезок
времени распадаются, создавая два (или
три) фотона (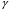 -
кванта).
-
кванта).
Энергию
связи (ионизации) можно вычислить,
воспользовавшись формулой (2.61) при
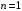 ,
но в качестве приведенной массы необходимо
использовать половину массы электрона
(массы позитрона и электрона одинаковы):
,
но в качестве приведенной массы необходимо
использовать половину массы электрона
(массы позитрона и электрона одинаковы):
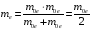 .
.
Следовательно,
из формулы (2.61) получаем
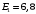 эВ.
эВ.
2.6. Энергетический спектр атомов щелочных металлов
Структура
электронной оболочки атома щелочного
металла очень характерна. Если атом
имеет всего
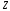 электронов, то
электронов, то
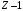 электронов образуют структуру атома
благородного газа, а последний электрон
связан с ядром и этими электронами очень
слабо. Следовательно, щелочные атомы
похожи на водородоподобные ионы, но не
совсем. Внешний (валентный) электрон
немного деформирует оболочку внутренних
электронов и искривляет их поле. Поэтому
потенциальную энергию поля, в котором
движется валентный электрон, можно
предоставить в виде ряда:
электронов образуют структуру атома
благородного газа, а последний электрон
связан с ядром и этими электронами очень
слабо. Следовательно, щелочные атомы
похожи на водородоподобные ионы, но не
совсем. Внешний (валентный) электрон
немного деформирует оболочку внутренних
электронов и искривляет их поле. Поэтому
потенциальную энергию поля, в котором
движется валентный электрон, можно
предоставить в виде ряда:
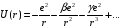 ,
(2.90)
,
(2.90)
где второй и дальнейшие члены оказываются поправками, которые учитывают отличие поля щелочного атома от поля атома водорода. Если ограничиться лишь первой поправкой, то расчеты проводятся аналогично разд.2.2, только вместо уравнения (2.38) получим
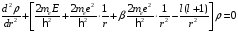 .
(2.91)
.
(2.91)
Введем обозначение
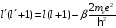 .
(2.92)
.
(2.92)
Решение квадратного уравнения (2.92) имеет вид
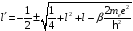 .
.
Отрицательные
значения
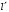 отбрасываем,
поскольку они приводят к бесконечности
волновую функцию в нуле. Поэтому выражение
для
отбрасываем,
поскольку они приводят к бесконечности
волновую функцию в нуле. Поэтому выражение
для
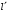 принимает
следующий вид
принимает
следующий вид
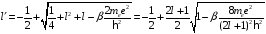 .
(2.93)
.
(2.93)
Поскольку
в (2.91) член с
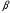 учитывает
поправку на искажение кулоновского
поля, а оно, как мы допускаем, мало, то
учитывает
поправку на искажение кулоновского
поля, а оно, как мы допускаем, мало, то
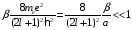 .
(2.94)
.
(2.94)
и
окончательно можно предоставить
выражение для
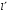 в
следующем виде:
в
следующем виде:
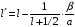 .
(2.95)
.
(2.95)
При
использовании замены согласно (2.92)
уравнение (2.91) приобретает такой же вид,
как и уравнение Шредингера (2.38) для
радиальной части волновой функции атома
водорода. Главное квантовое число
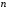 заменяется числом
заменяется числом
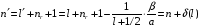 ,
(2.96)
,
(2.96)
где
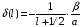 ,
(2.97)
,
(2.97)
а формула для энергетических уровней валентного электрона приобретает вид:
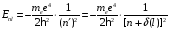 .
(2.98)
.
(2.98)
Главное
отличие энергии атома щелочного металла
от энергии атома водорода заключается
в зависимости уровня энергии не только
от главного квантового числа n,
но и от орбитального квантового числа
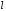 :
уровни энергии, которые отвечают одному
и тому же главному квантовому числу, но
с разными орбитальными числами, не
совпадают друг с другом.
:
уровни энергии, которые отвечают одному
и тому же главному квантовому числу, но
с разными орбитальными числами, не
совпадают друг с другом.
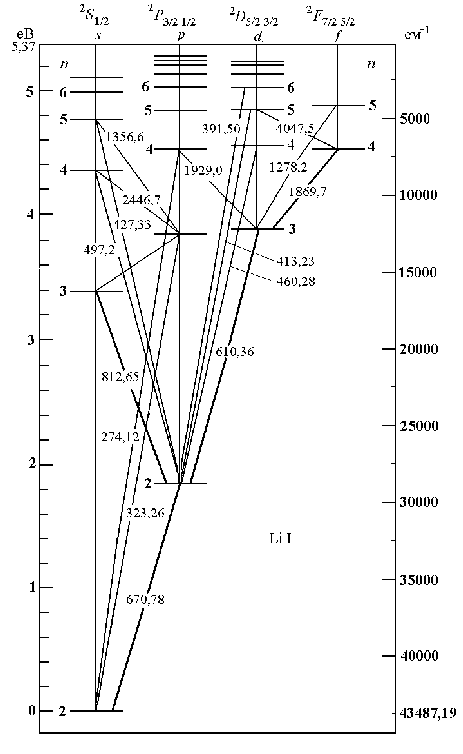
На
рис.2.5 приведенная схема уровней атома
лития и наиболее интенсивных переходов
между ними. Самым низким уровнем энергии
является
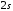 –состояние
(
–состояние
(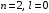 ),
поскольку состояние с
),
поскольку состояние с
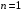 уже занято двумя электронами, которые
образуют остов водородоподобного атома.
Излучение возможно лишь в случае
разрешенных переходов. Правила отбора
имеют следующий вид:
уже занято двумя электронами, которые
образуют остов водородоподобного атома.
Излучение возможно лишь в случае
разрешенных переходов. Правила отбора
имеют следующий вид:
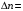 любое,
любое,
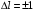 ,
(2.99)
,
(2.99)
то есть главное квантовое число может изменяться на любую величину, а орбитальное квантовое число – лишь на единицу.
Переходы
из выше расположенных уровней в состояние
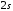 образуют
главную
серию,
из
образуют
главную
серию,
из
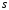 –состояний
в
–состояний
в
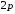 -состояние
– резкую
серию,
из d–состояний
в
-состояние
– резкую
серию,
из d–состояний
в
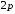 –состояние
– диффузную
серию.
–состояние
– диффузную
серию.
Схемы уровней других щелочных металлов имеют аналогичную структуру.
|
|
|
Рис.2.5. Спектр лития (длина волны в нм) |
1 Лежандр Андриен Мари (1752-1833) – французский математик. Научные труды по теории чисел, эллиптическим интегралам, геометрии и др.
2 При решении задачи будем пользоваться абсолютной системой единиц. В окончательном результате перейдем к СИ.
3 Лагерр Эдмон-Никола (1834-1886) – французский математик. Научные труды по геометрии, непрерывной дроби и др.
4 Лайман Теодор (1874-1954) – американский физик-экспериментатор. Специалист в области оптики и спектроскопии.
5 Бальмер Иоган Якоб (1825-1898) – швейцарский физик и математик. Работы в области спектроскопии.
6 Пашен Фридрих (1865-1947) – немецкий физик-экспериментатор. Основные работы посвящены атомной спектроскопии и квантовой теории излучения.

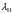 ,
нм
,
нм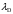 ,
нм
,
нм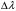 ,нм
,нм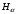
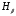
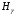
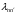 ,
нм
,
нм