2.4. Волновые функции атома водорода и распределение электронной плотности

Рассмотрим детальнее квантовые состояния и соответствующие собственные волновые функции :

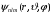. (2.76)

Нормированные волновые функции для некоторых состояний водородоподобных атомов (для водорода 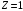) приведены в табл.2.1.

Квадрат абсолютного значения представляет вероятность того, что при определении положения электрона в квантовом состоянии 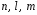он будет найден в некотором объеме возле точки с координатами 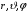(рис. 2.2):

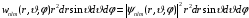. (2.77)

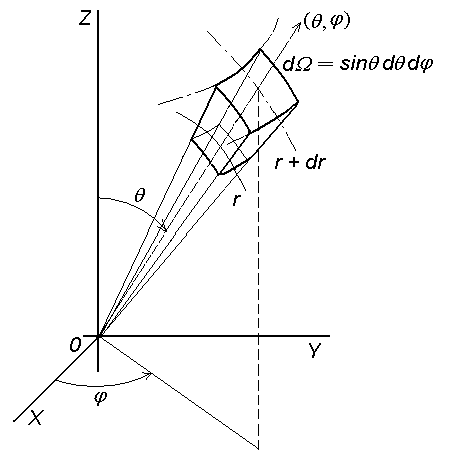
Обозначив через 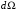элемент телесного угла 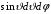и используя формулы (2.3) и (2.55), запишем вероятность в виде

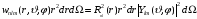. (2.78)

Интегрируя по всем углам 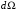, мы получим вероятность найти электрон между двумя сферами с радиусами и 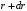. Обозначим эту вероятность через

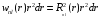. (2.79)

Таблица 2.1

n	l	m	Нормируемая	Состояние
1	0	0		1s
2	0	0		2s
2	1	0		2p
		1
3	0	0		3s
3	1	0		3p
		1
3	2	0		3d
		1
		2

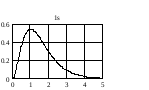
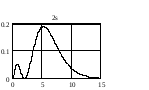
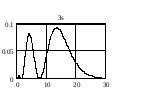
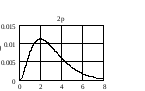
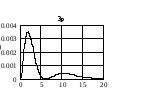
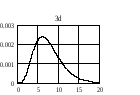
На рис. 2.3 приведено распределение плотности вероятности для различных состояний в зависимости от расстояния 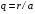до центра. Числа на кривых определяют значение чисел 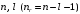. Из графиков можно видеть, что радиальное квантовое число определяет число узлов волновой функции .

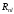Выясним теперь значение введенной выше длины 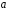. Для основного квантового состояния (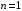) имеем

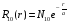. (2.80)

Следовательно,

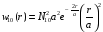. (2.81)

Рис.2.2. Сферические координаты

Плотность вероятности
Нормируемый радиус q=r/a
Рис.2.3. Распределение плотности вероятности для разных состояний атома водорода

Максимальное значение этой вероятности имеет место при 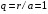. Отсюда следует, что в состоянии 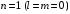наиболее вероятно найти электрон при

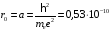м . (2.82)

Это есть радиус первой орбиты Бора, величина которого впервые была получена Н.Бором из старой теории квантования.

Рассмотрим теперь распределение по углам. Если интегрировать по от 0 до 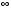, то получим вероятность того, что электрон находится в телесном угле 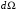вокруг луча 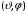. Воспользовавшись нормировкой (2.10) для 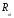, получим

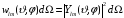. (2.83)

Из вида функции 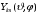(2.20) следует, что вероятность не зависит от угла 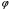и равняется

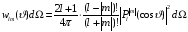. (2.84)

Следовательно, распределение по углам имеет сферическую симметрию. На рис.2.4 приведены полярные диаграммы плотности вероятности для различных состояний 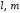. Величина 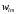откладывается по радиус-вектору. При 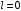, 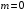вероятность

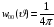(2.85)

не зависит от угла 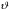, и поэтому мы имеем сферическую симметрию. Состояние, в котором момент импульса равняется нулю (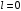), называют s-состоянием, соответствующий терм называют s-термом. Это состояние характеризуется сферической симметрией.

Состояние с 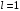(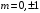) называют p- состоянием, а соответствующий терм – p-термом. Вероятность в этом случае определяется функциям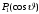и и 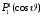. Воспользовавшись (2.16) и (2.17), получим из (2.84)

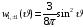, (2.86)

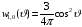. (2.87)

Состояние с 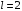(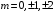) называют d- состоянием, а соответствующий терм – d-термом. Как и в предыдущем случае получим

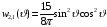. (2.88)

Вид распределения вероятностей (рис.2.4) позволяет нам получить некоторое представление о форме атома в различных состояниях. Эта форма определяется значением орбитального числа 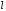, а магнитное число определяет ориентацию атома в пространстве.

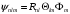
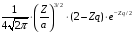
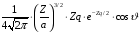
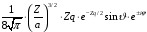
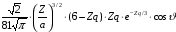
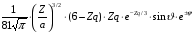
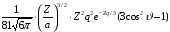
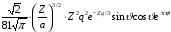
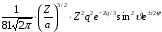
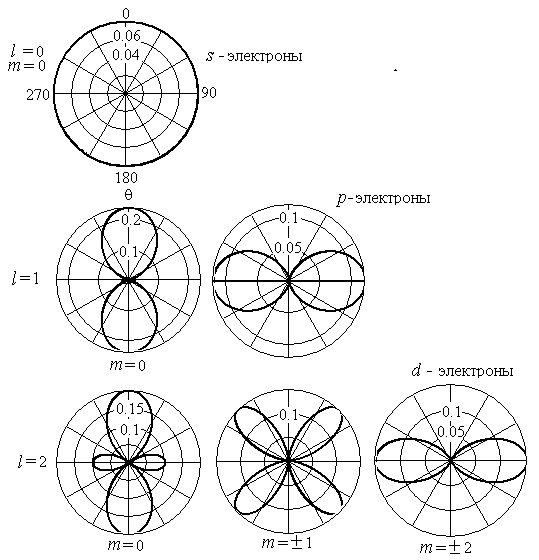
Рис.2.4. Угловое распределение электронов 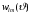для s-, p- и d-состояний.