- •«Физические основы электронной техники. Квантовая механика»
- •2. Движение микрочастицы в поле центральной
- •2.1. Поле центральной симметрии
- •2. 2. Атом водорода. Радиальная часть волновой функции
- •2.3. Схема уровней энергии и спектр атома водорода
- •2.4. Волновые функции атома водорода и распределение электронной плотности
- •2.5. Изотопический сдвиг и водородоподобные ионы
- •2.6. Энергетический спектр атомов щелочных металлов
2.3. Схема уровней энергии и спектр атома водорода
Энергетические
уровни атома водорода (заряд ядра
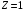 )
можно
вычислить, воспользовавшись формулами
(2.40), (2.41) и (2.51):
)
можно
вычислить, воспользовавшись формулами
(2.40), (2.41) и (2.51):
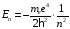 ,
(2.60)
,
(2.60)
где
главное квантовое число
 принимает значения
принимает значения
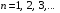 .
.
Перейдя к международной системе (СИ), получим
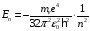 ,
(2.61)
,
(2.61)
где
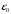 – диэлектрическая постоянная,
– диэлектрическая постоянная,
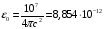 Ф/м.
Ф/м.
Энергия
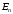 ,
как следует из (2.61), зависит только от
главного квантового числа n.
Когда оно задано, то из
,
как следует из (2.61), зависит только от
главного квантового числа n.
Когда оно задано, то из
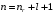 (см.
формулу 2.51) вытекает, что орбитальное
квантовое число может принимать лишь
такие значения:
(см.
формулу 2.51) вытекает, что орбитальное
квантовое число может принимать лишь
такие значения:
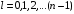 .
(2.62)
.
(2.62)
Магнитное
квантовое число при заданном
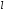 пробегает
следующие значения
пробегает
следующие значения
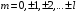 .
(2.63)
.
(2.63)
Одновременно
с энергией атома принимают определенные
значения момент импульса
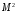 та его проекция
та его проекция
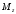 на некоторое выделенное направление
на некоторое выделенное направление
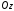 :
:
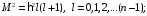 (2.64)
(2.64)
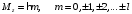 .
(2.65)
.
(2.65)
Таким
образом, динамическое значение главного
квантового числа
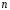 ,
орбитального
,
орбитального
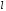 и магнитного
и магнитного
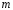 заключается в том, что они определяют
величину энергии, величину момента
импульса и величину проекции момента
импульса.
заключается в том, что они определяют
величину энергии, величину момента
импульса и величину проекции момента
импульса.
Три
величины
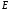 ,
,
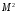 и
и
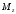 полностью определяют волновую функцию
полностью определяют волновую функцию
 и
поэтому образуют полный набор величин.
Количество их, как и должно быть, равняется
трем, то есть числу степеней свободы.
и
поэтому образуют полный набор величин.
Количество их, как и должно быть, равняется
трем, то есть числу степеней свободы.
Воспользовавшись
значениями постоянных
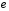 ,
,
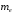 и
и
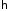 ,
вычислим квантовые уровни энергии
электрона, который движется в поле ядра
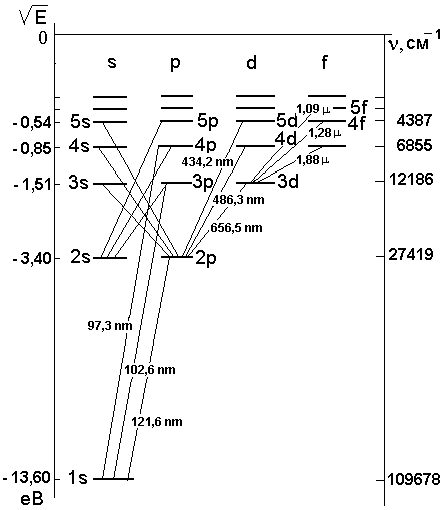
водорода (протона). Эти уровни показаны
на рис.2.1.
,
вычислим квантовые уровни энергии
электрона, который движется в поле ядра
водорода (протона). Эти уровни показаны
на рис.2.1.
Подсчитаем,
сколько различных волновых функций
принадлежит квантовому уровню
 .
Для каждого
.
Для каждого
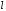 мы имеем
мы имеем
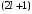 функций,
которые отличаются числом
функций,
которые отличаются числом
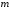 .
Но
.
Но
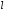 изменяется от 0 до
изменяется от 0 до
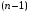 ,
поэтому полное количество функций будет
,
поэтому полное количество функций будет
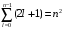 . (2.66)
. (2.66)
Таким
образом, каждому квантовому уровню
энергии
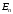 принадлежит
принадлежит
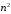 различных
состояний. В этом случае мы имеем дело
со случаем
различных
состояний. В этом случае мы имеем дело
со случаем
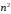 –
кратного вырождения. Вырождение по
числу
–
кратного вырождения. Вырождение по
числу
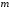 называют
нормальным,
по числу
называют
нормальным,
по числу
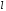 – случайным.
– случайным.
Переход электрона между уровнями сопровождается излучением или поглощением кванта энергии:
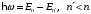 .
(2.67)
.
(2.67)
|
|
|
Рис.2.1. Диаграмма уровней атома водорода |
Используя (2.60), получим из последней формулы
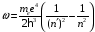 .
(2.68)
.
(2.68)
Эта
формула определяет частоту света,
который излучается или поглощается
атомом водорода. Величина
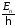 называется термом. Разность термов
определяет частоты. Для атома водорода
терм
называется термом. Разность термов
определяет частоты. Для атома водорода
терм
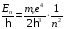 .
(2.69)
.
(2.69)
В оптической спектроскопии чаще употребляют термин «спектральный терм». Под этим понимается значение
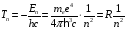 ,
(2.70)
,
(2.70)
которое отсчитывается для атомов от границы ионизации и выражается в см - 1.
Величина
 называется
постоянной Ридберга
называется
постоянной Ридберга
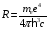 или
или
 (в СИ). (2.71)
(в СИ). (2.71)
В
случае, когда
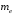 равняется
массе покоя электрона
равняется
массе покоя электрона
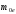 (случай бесконечно тяжелого ядра
(случай бесконечно тяжелого ядра
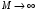 ),
постоянная
),
постоянная
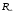 равна
равна
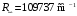 ,
(2.72)
,
(2.72)
а для атома водорода
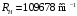 .
(2.73)
.
(2.73)
Спектральная
частота перехода
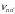 между уровнями
между уровнями
 и
и
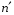 составляет
составляет
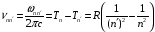 .
(2.74)
.
(2.74)
Длина
волны перехода между уровнями
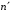 и
и
 определяется
формулой
определяется
формулой
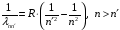 .
(2.75)
.
(2.75)
Для
атома водорода
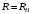 .
.
На диаграмме рис.2.1 справа нанесены числа спектральных термов.
Различные
серии в спектре излучения атома водорода
возникают в результате перехода электрона
с верхних уровней на нижние. Переходы
на уровень
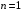 образуют серию Лаймана4
(УФ диапазон), на уровень
образуют серию Лаймана4
(УФ диапазон), на уровень
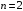 – серию Бальмера5
(видимый), на уровень
– серию Бальмера5
(видимый), на уровень
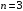 –
серию Пашена6
(ИК диапазон) и т.д.
–
серию Пашена6
(ИК диапазон) и т.д.
Спектральные линии серии Бальмера обозначают буквами
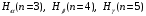 и т.д.
и т.д.
Спектры
водородоподобных ионов
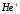 ,
,
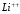 и т.п. имеют такой же вид, как и рассмотренный
спектр водорода, но все линии смещаются
в область более коротких волн, поскольку
в этих случаях постоянную Ридберга
необходимо увеличить в
и т.п. имеют такой же вид, как и рассмотренный
спектр водорода, но все линии смещаются
в область более коротких волн, поскольку
в этих случаях постоянную Ридберга
необходимо увеличить в
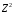 раз.
раз.
Электрон на уровнях с числом n может находиться в различных квантовых состояниях в зависимости от орбитального квантового числа l.