4.2.4. Проверка напряжений изгиба зубьев шестерни и колеса:

Проверяем напряжения изгиба зубьев колеса:

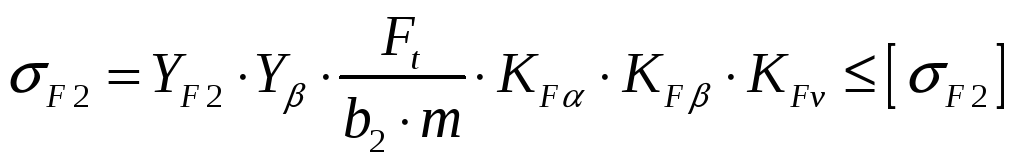, где

- коэффициент, учитывающий распределение нагрузки между зубьями. Для косозубых передач зависит от степени точности, и т.к . степень точности 9 :

,

- коэффициент неравномерности нагрузки по длине зуба. Т. к. колёса прирабатывающиеся, то

,

- коэффициент динамической нагрузки. Определяется интерполированием по таблице в зависимости от окружной скорости колёс и класса точности передачи:

,

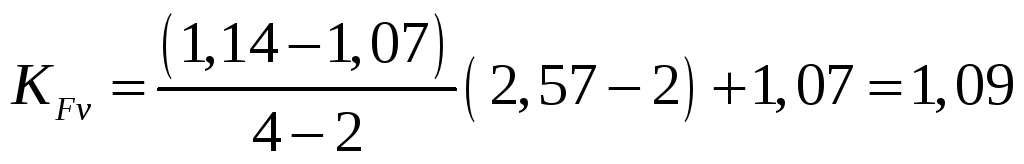- коэффициент формы зуба колеса. Для прямозубых передач

0н зависит от числа зубьев шестерни и колеса:

- коэффициент, учитывающий наклон зуба. Для прямозубых

передач

Вычисляем напряжения изгиба зубьев колеса:

.

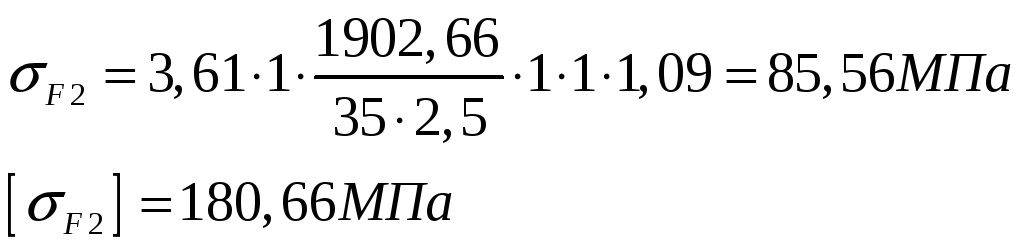Проверяем напряжения изгиба зубьев шестерни:

,

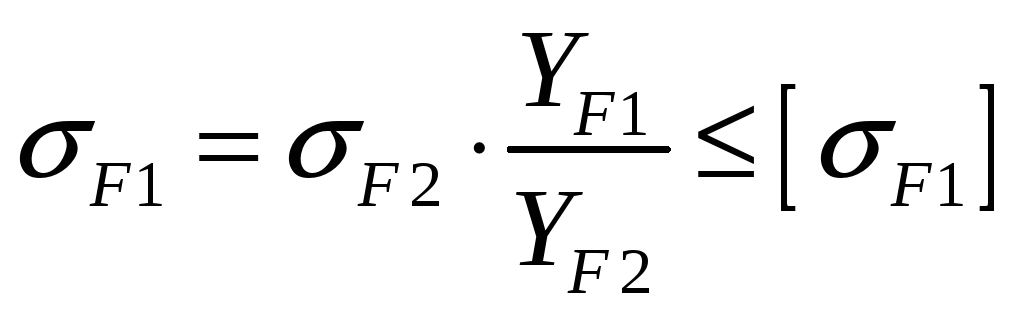Вычисляем напряжения изгиба зубьев колеса:

.

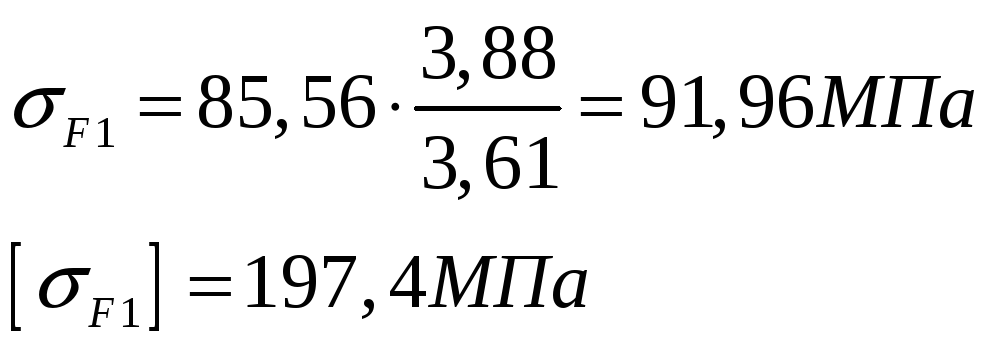Получили, что значительно меньше . Это допускаемо, т. к. нагрузочная способность большинства зубчатых передач ограничивается контактной прочностью.

4.3Расчет клиноременной передачи.

4.3.1. Выбор сечения клинового ремня

В зависимости от частоты вращения меньшего шкива (), передаваемой мощности ().

По номограмме 7.3. (С.А. Чернавский «Курсовое проектирование деталей машин») принимаем сечение клинового ремня --- Б.

4.3.2.Диаметр ведущего шкива

Определяем минимально допустимый диаметр ведущего шкива по формуле, в зависимости от вращающего момента на валу двигателя .

_{Результат округляем до стандартного значения (ГОСТ 17383-73):}

4.3.3.Диаметр ведомого шкива

Диаметр ведомого шкива определим по формуле:

;

Где u-передаточное число клиноременной передачи;

коэффициент скольжения;

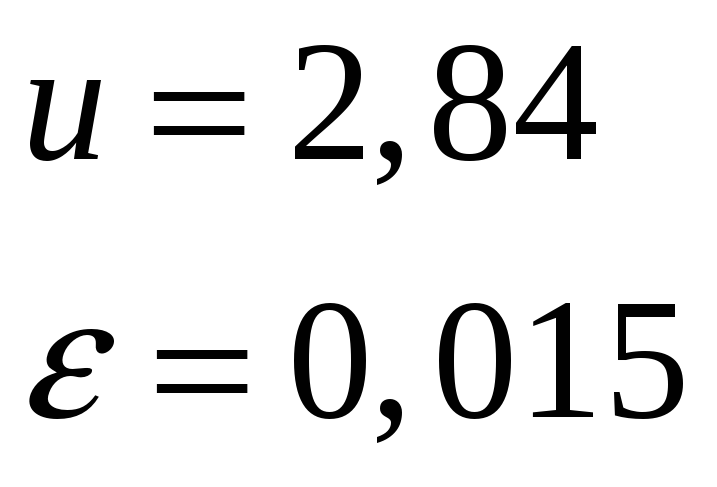
Тогда:

Округляя до стандартного значения по табл. К40, получим:

4.3.4.Фактическое передаточное число открытой передачи

Фактическое передаточное число определяем по формуле:

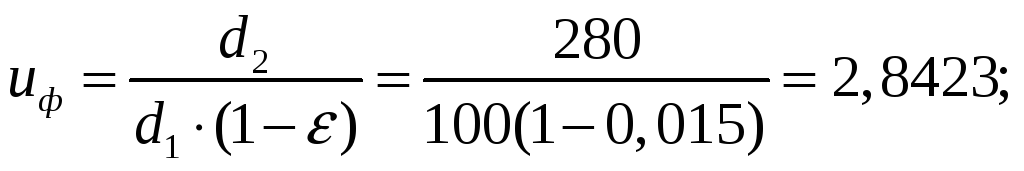
Проверяем его отклонение от заданного u:

Значит, условие выполняется.

4.3.5.Ориентировочное межосевое расстояние

Минимальное межосевое расстояние определяется по формуле:

Где h-высота сечения ремня, определяется по таблице, и равно

, тогда

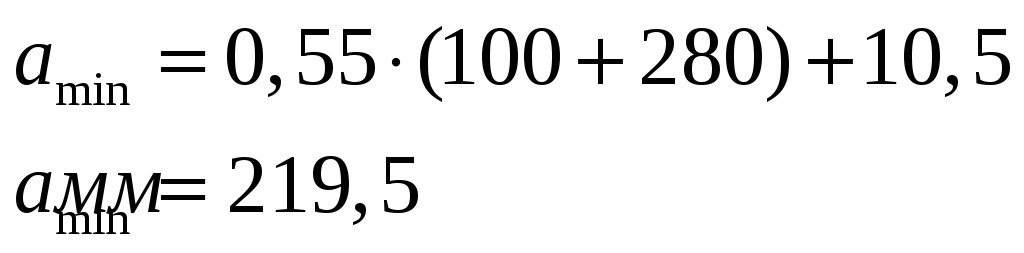
Найдём максимальное межосевое расстояние по формуле:

Принимаем предварительно близкое значение: а=220

4.3.6.Расчётная длина ремня

Расчётная длина ремня:

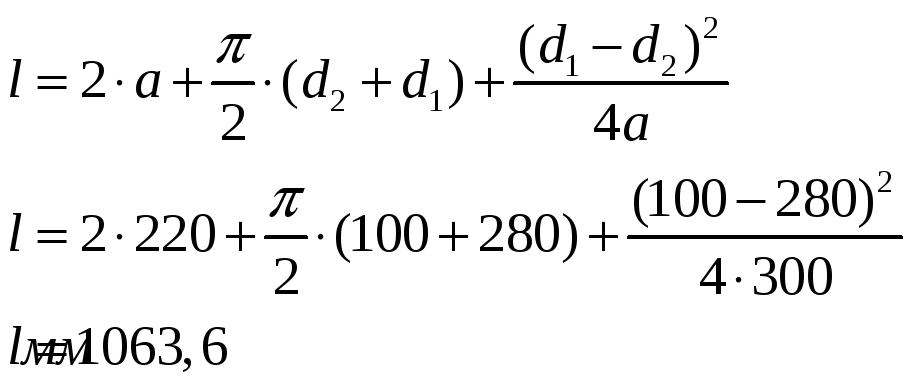
Округляем до ближайшего стандартного значения

4.3.7.Уточнение межосевого расстояния

Уточненное значение межосевого расстояния, с учетом стандартной длины ремня:

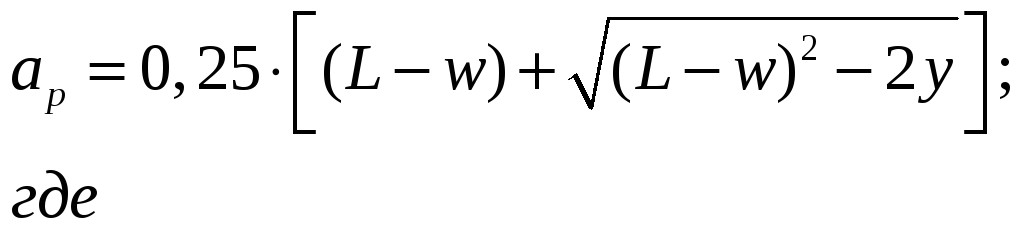
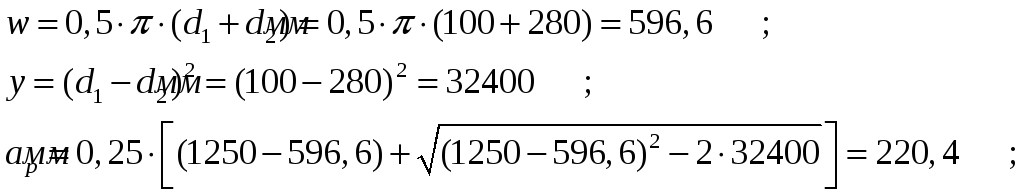
При монтаже передачи необходимо обеспечить возможность уменьшения межосевого расстояния на 0,01L=0,01х1120=11,2мм, для облегчение надевания ремней на шкивы и возможности его увеличения его на 0,025L=0,025х1120=28мм, для увеличения натяжения ремней.

4.3.8.Угол обхвата ведущего шкива

Угол обхвата ведущего шкива определяется по формуле:

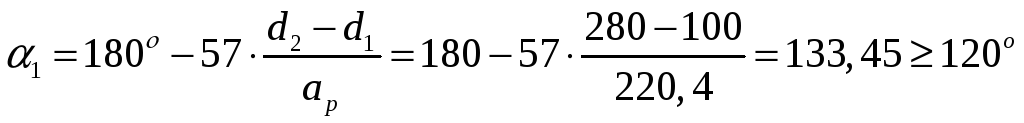
4.3.9.Скорость ремня

Определяем скорость ремня по формуле:

;

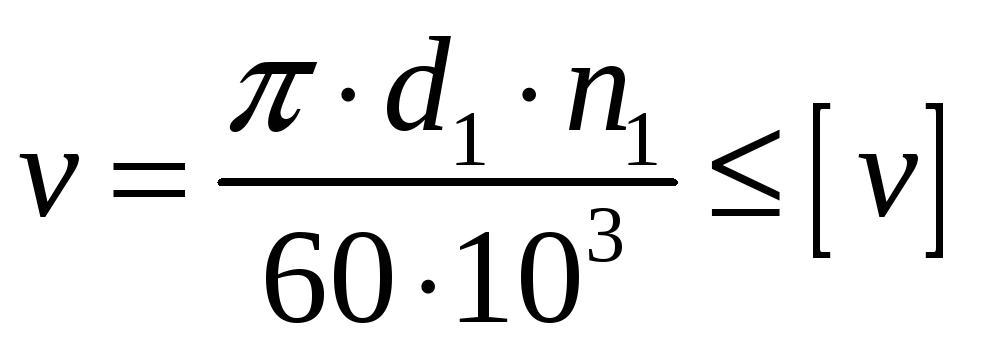Где d1-диаметр ведущего шкива, мм;

n1-частота вращения, об\мин;

[v]-допускаемая скорость, для клиновых ремней-25м\с;

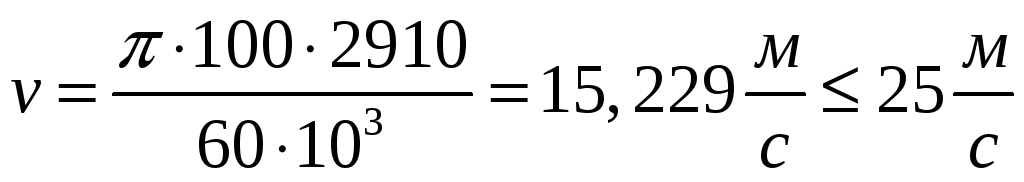
4.3.10.Частота пробега ремня

Частота пробега ремня определяется по формуле:

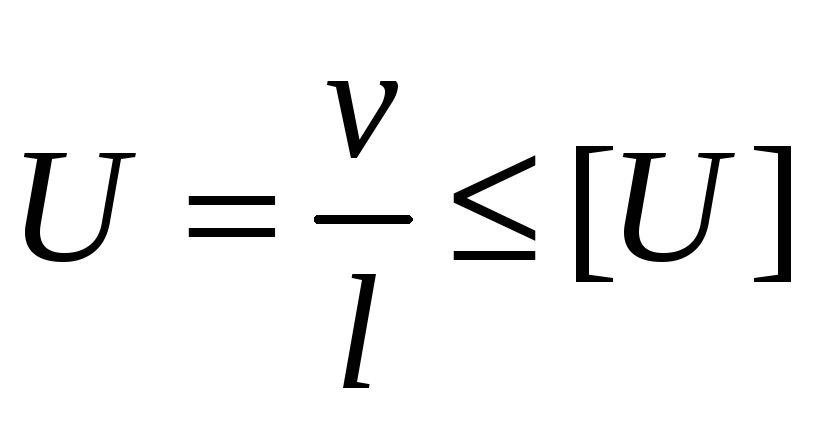
Где [U]-допускаемая частота пробега ремня, для клинового ремня при

нормальном сроке службы- 30 с¯¹;

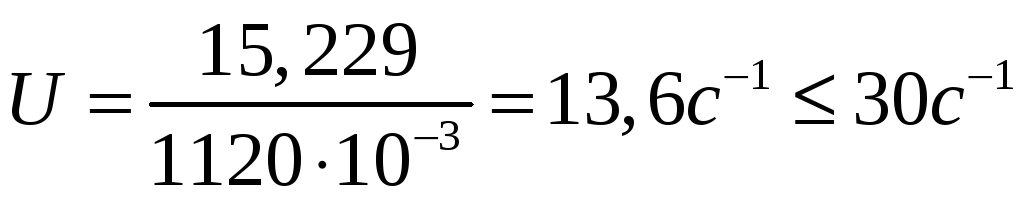
4.3.11.Необходимое число ремней

Необходимое число ремней для передачи данной мощности, определяется по формуле:

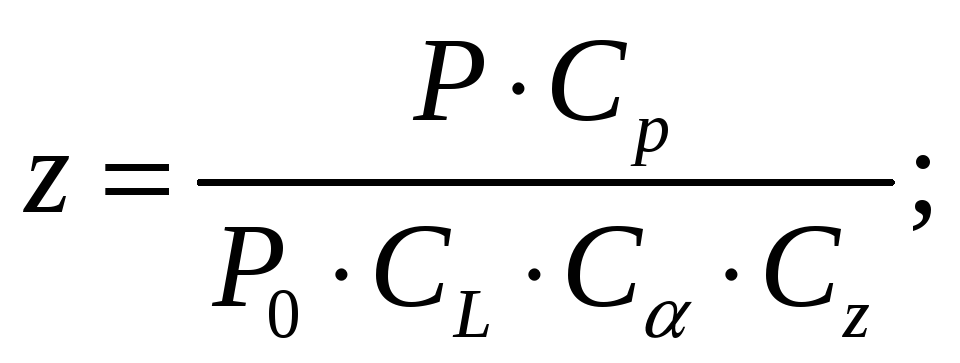
Где

Р0-мощность, допускаемая для передачи одним ремнем,

Р0=1,48кВт;

СL- коэффициент, учитывающий влияние длины ремня,

СL=0,88;

Cp- коэффициент динамичности нагрузки, при спокойной нагрузке,

Cp =1;

Са- коэффициент угла обхвата, при угле 156,38градусов, Са=0,935;

Сz –коэффициент, учитывающий число ремней в передаче,

При z=4..6, Сz=0,90;

Тогда

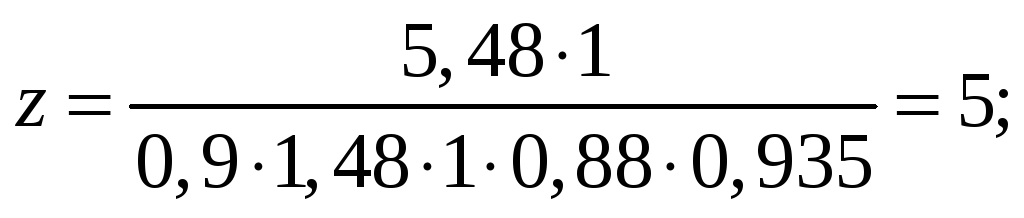
Принимаем Z=5

4.3.12.Натяжение ветви клинового ремня

Определяем по формуле:

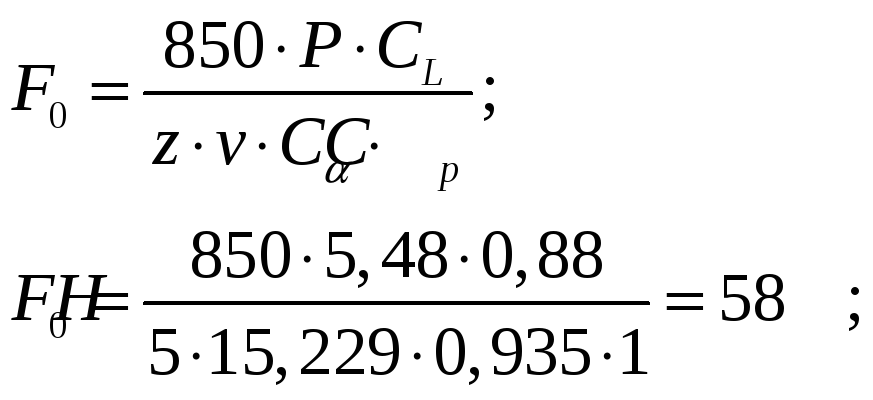
4.3.13.Окружная сила

Определяем окружную силу передаваемую комплектом клиновых ремней по формуле

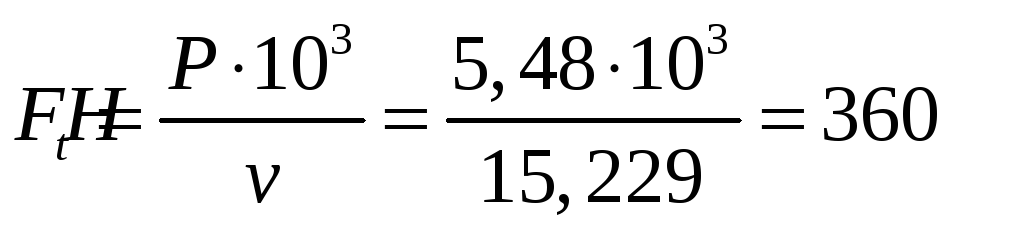
4.3.14. Силы натяжения ведущей и ведомой ветвей

Для одного клинового ремня

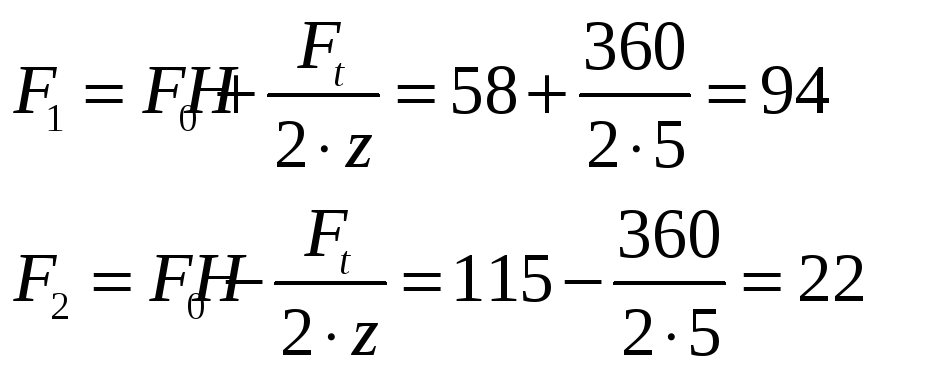
4.3.15. Сила давления на валы

Давление на валы определяем по формуле:

4.3.16. Ширина шкивов

Определяется по формуле:

4.4.Проверочный расчёт

4.4.1.Прочность одного клинового ремня

Проверяем прочность одного клинового ремня по максимальным напряжениям в сечении ведущей ветви

Где σ1-напряжение растяжения, для клинового ремня:

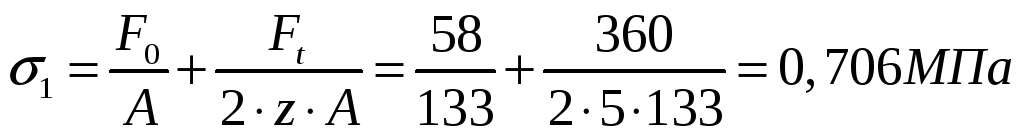
σИ- напряжение изгиба, для клинового ремня:

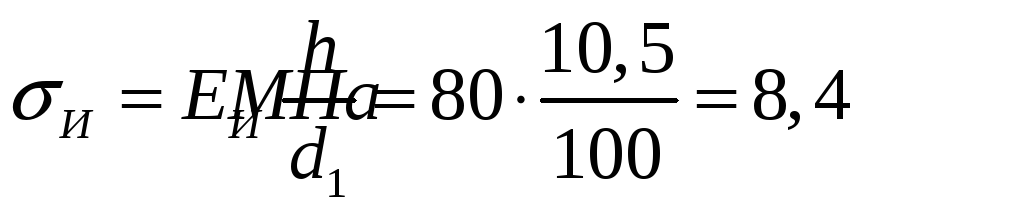
σv – напряжение от центробежных сил:

[σ]р – допускаемое напряжение, для клинового ремня равна 10МПа

Тогда:

Значит условие выполняется.