
- •Оглавление
- •Введение.
- •2. Выбор электродвигателя и кинематический расчет механизма.
- •2.1. Коэффициент полезного действия редуктора
- •2.2. Расчёт требуемой мощности и выбор электродвигателя
- •3.1 Определение мощностей на валах
- •1.8. Таблица полученных результатов для валов
- •4. Расчет передач.
- •4.1. Расчет цилиндрической косозубой передачи.
- •4.1.1 Выбор твёрдости, термообработки и материала колёс
- •4.1.2. Допускаемые контактные напряжения
- •4.1.3. Допускаемые напряжения изгиба
- •4.1.4. Межосевое расстояние
- •4.1.5. Модуль зацепления
- •4.1.6. Суммарное число зубьев шестерни и колеса
- •4.2.2.Проверка пригодности заготовок
- •4.2.4. Проверка напряжений изгиба зубьев шестерни и колеса:
- •4.3Расчет клиноременной передачи.
- •4.4.2.Табличный отчет
- •18.Литература:
4.1.4. Межосевое расстояние
Определяем межосевое расстояние:
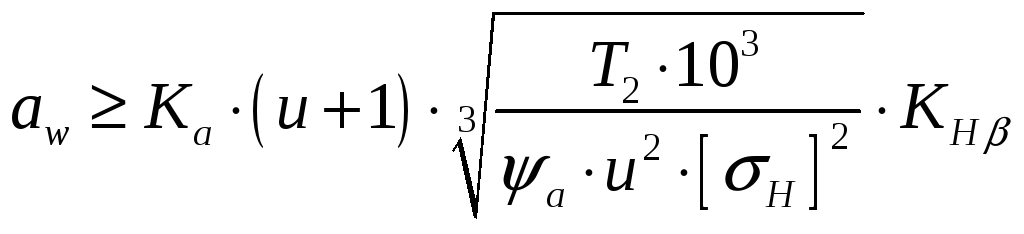 .
.
Определяем величины в вышезаписанном выражении:
![]() - вспомогательный
коэффициент, для прямозубых передач
- вспомогательный
коэффициент, для прямозубых передач
![]() ,
,
![]() - коэффициент
ширины венца колеса, для шестерни
выбираем
- коэффициент
ширины венца колеса, для шестерни
выбираем
![]() ,
,
T2 - вращающий момент на валу, T2=235,628 Н·м,
![]() - коэффициент
неравномерности нагрузки по длине зуба,
для прирабатывающихся зубьев
- коэффициент
неравномерности нагрузки по длине зуба,
для прирабатывающихся зубьев
![]() .
.
 .
.
Из 1-ого ряда
выбираем стандартное значение для
межосевого расстояния
![]() .
.
4.1.5. Модуль зацепления
Модуль зацепления определяем по формуле:
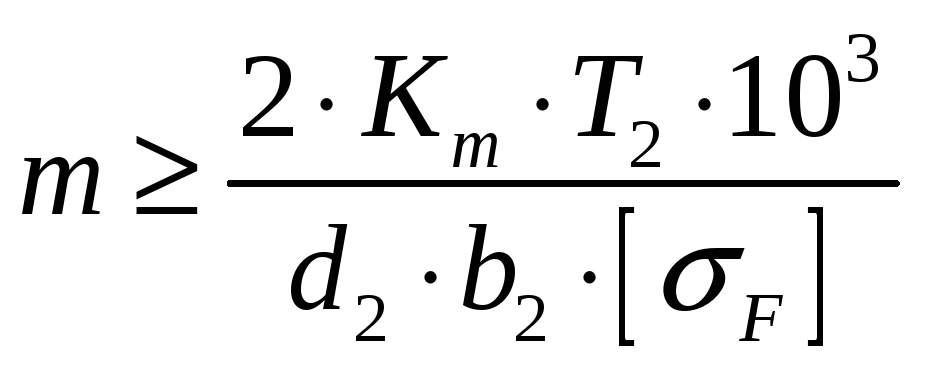 ,
где
,
где
![]() - вспомогательный
коэффициент, для прямозубых передач
- вспомогательный
коэффициент, для прямозубых передач
![]() .
.
d2 - делительный диаметр колеса, определяется по формуле:
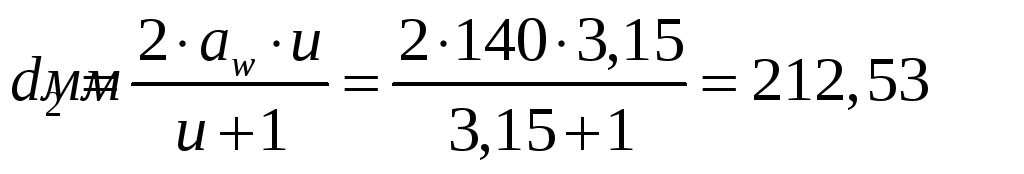 ,
,
b2 - ширина венца колеса:
![]() ,
,
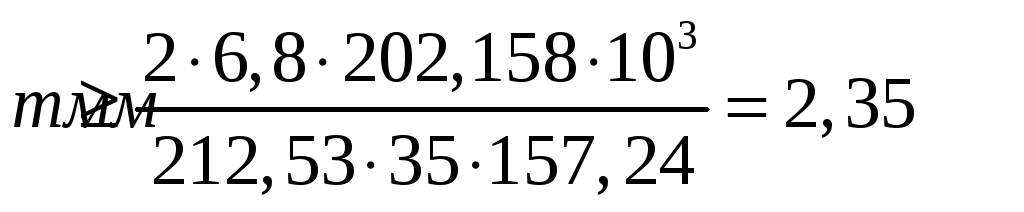 .
.
По ГОСТ 95.63-80 из первого ряда выбираем стандартное значение модуля зацепления:
![]() .
.
4.1.6. Суммарное число зубьев шестерни и колеса
Для прямозубых колёс суммарное число зубьев вычисляем по формуле
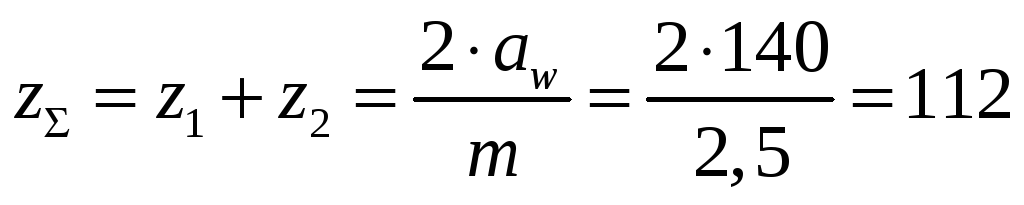 ,
,
результат округляем в меньшую сторону до целого числа, значит,
![]() .
.
4.1.7. Число зубьев шестерни и колеса
Число зубьев шестерни равно:
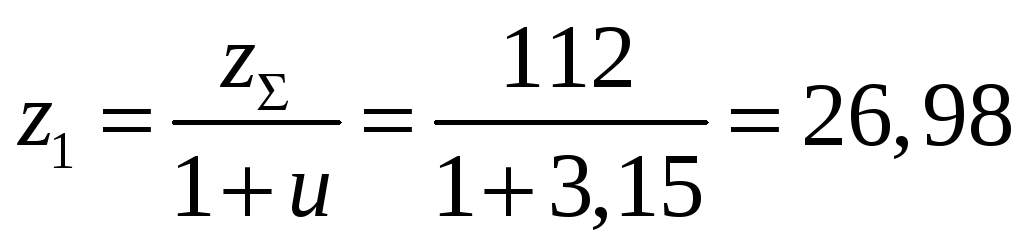 ,
,
полученное значение округляем до ближайшего целого числа, следовательно:
![]() .
.
Соответственно, число зубьев колеса равно:
![]()
4.1.8. Фактическое передаточное число
Определяем фактическое передаточное отношение редуктора :
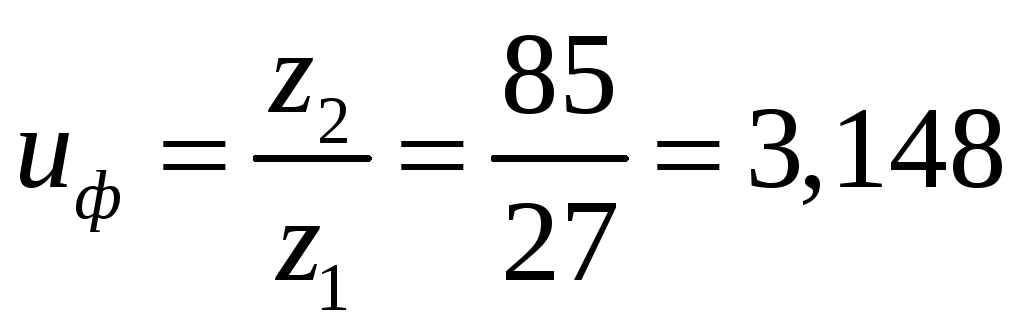 .
.
Проверяем отклонение фактического передаточного отношения от заданного, оно не должно превышать 4%:
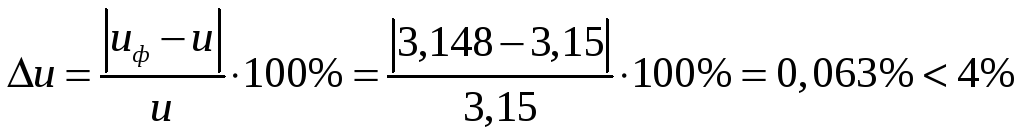 .
.
Т. е. условие выполняется.
4.1.9. Фактическое межосевое расстояние
Фактическое межосевое расстояние для прямозубых передач определяется по формуле:
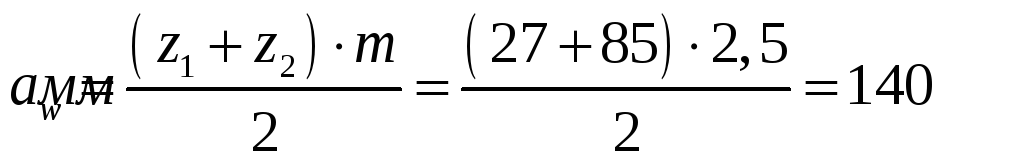 .
.
4.1.10. Основные геометрические параметры передачи:
Делительный диаметр шестерни:
![]() .
.
Делительный диаметр колеса:
![]() .
.
Диаметр вершин зубьев шестерни:
![]() .
.
Диаметр вершин зубьев колеса:
![]() .
.
Диаметр впадин зубьев шестерни:
![]() .
.
Диаметр впадин зубьев колеса:
![]() .
.
Ширина венца колеса:
![]() .
.
![]() .
.
Ширина венца шестерни определяется по формуле :
![]() .
.
Чтобы значение ширины венца шестерни было стандартным, параметр определяем по формуле:
![]() .
.
4.1.11. Основные геометрические параметры заготовок
Диаметр заготовки шестерни
![]()
Ширина заготовки колеса
![]()
4.2. Проверочный расчёт зубчатой передачи
4.2.1.Проверка межосевого расстояния
Межосевое расстояние проверим по формуле:
![]()
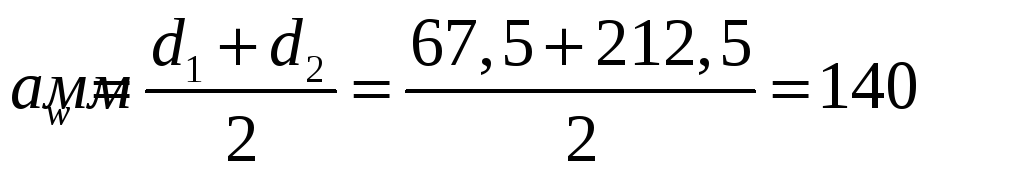 ;
;
4.2.2.Проверка пригодности заготовок
Проверим пригодность заготовок по табл.3.2, «Курсовое проектирование деталей машин» А.Е. Шейнблит.
![]()
![]()
![]()
![]()
![]()
4.2.3. Проверка контактных напряжений
Проверку контактных напряжений ведём по формуле:
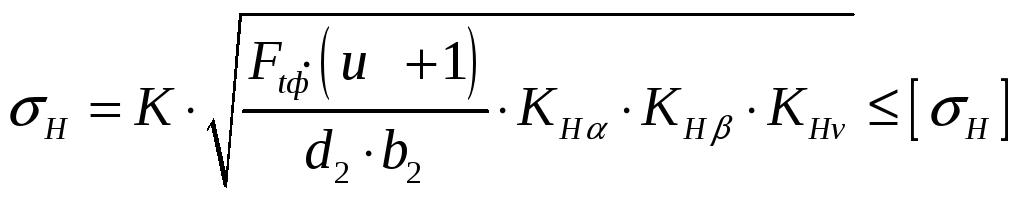 ,
где
,
где
K - вспомогательный коэффициент. Для прямозубых передач K=436,
Ft - окружная сила. Определяем по формуле:
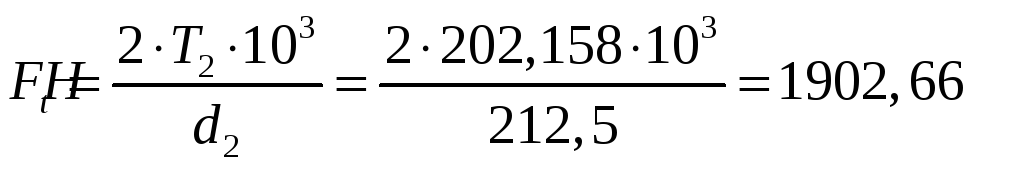 ,
,
![]() - коэффициент,
учитывающий распределение нагрузки
между зубьями. Для прямозубых передач
- коэффициент,
учитывающий распределение нагрузки
между зубьями. Для прямозубых передач
![]()
![]() - коэффициент
динамической нагрузки, зависящий от
окружной скорости колёс и степени
точности передачи. Определяем окружную
скорость
- коэффициент
динамической нагрузки, зависящий от
окружной скорости колёс и степени
точности передачи. Определяем окружную
скорость
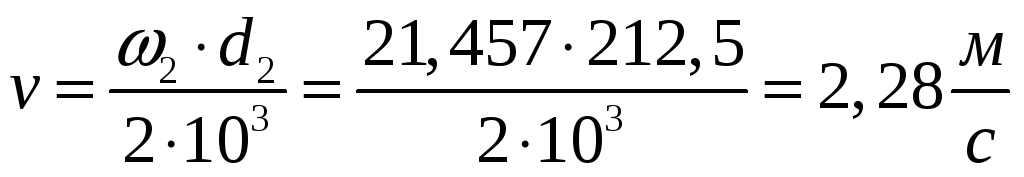 ,
,
Отсюда степень точности по табл. 4.2 принимаем равной 9.
Интерполированием определяем коэффициенты
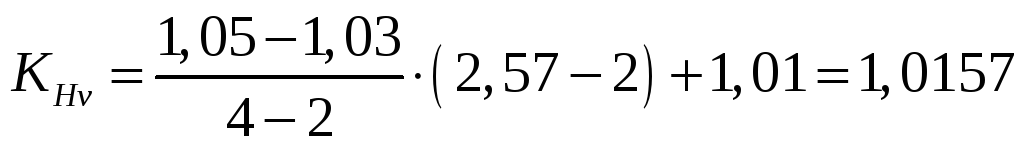 ,
,
![]()
(Т.к. степень точности мы приняли равной 9);
Определяем контактное напряжение:
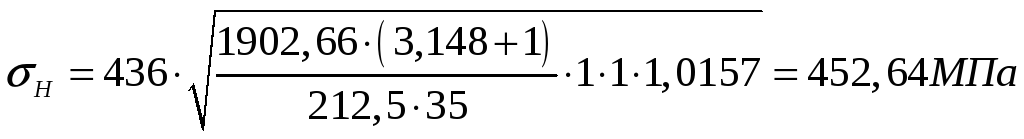
Т. к. контактное напряжение получилось меньше допускаемого, то определяем недогрузку передачи, которая должна быть не более 10% :
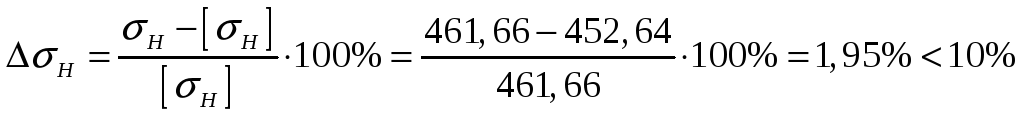 .
.
Значит, условие прочности выполняется.
