
- •1 Теоретические аспекты информационных технологий. 7
- •2 Сжатие информации 75
- •3 Многоканальная передача и уплотнение линий связи 124
- •Теоретические аспекты информационных технологий.
- •Теория сигналов и спектральный анализ
- •Управление колебаниями
- •Теория информации
- •Дискретизация и квантование.
- •Сжатие информации
- •Адаптивная дискретизация, разностная и дельта-модуляция.
- •Статистическое сжатие.
- •Сжатие динамического диапазона.
- •Эффективное кодирование
- •Модификации кодов Хафмана
- •Алгоритмы Лемпеля – Зива
- •Сжатие графических изображений
- •Видеостандарт mpeg
- •Многоканальная передача и уплотнение линий связи
- •Сравнение и анализ основных методов разделения каналов
- •Адресное разделение каналов.
- •Разделение каналов на основе псевдослучайных последовательностей
- •3.4. Комбинированное разделение каналов
-
Дискретизация и квантование.
Дискретизация - представление непрерывного колебания рядом значений, выбирающихся из непрерывного колебания с определенным шагом по времени. Величина шага выбирается в соответствии с теоремой Котельникова. Впервые она была сформулирована в 1933 г. на первом Всесоюзном съезде по вопросам техники реконструкции дела связи и развития слаботочной промышленности. Эта же теорема за рубежом независимо была доказана Найквистом, Шенноном и Уитеккером[2]. Сущность теоремы сводится к следующему. Если непрерывный сигнал ограничен сверху частотой fв (верхней частотой), его можно представить в виде ряда дискретных значений, взятых с интервалом по времени
|
|
(1.117) |
Не касаясь метода доказательства этой теоремы, который изложен в [15], приведём достаточное условие разложения, которое сводится к восстановлению непрерывного сообщения:
|
|
(1.118) |
Восстановление
непрерывного сообщения, как следует
из (1.118), сводится к суммированию
бесконечного ряда дискретных отсчетов
U(kt)
с весовой функцией вида
![]() .
Как следует из рис. 1.7 , функции в узлах,
кратных t,
обращаются в 0 все, кроме одной, для
которой t0
= kt.
Это означает, что в данных точках ряд
(1.118) в узлах вырождается в один член, то
есть, в этих точках значения непрерывного
сигнала представляются рядом (1.118)
абсолютно точно.
.
Как следует из рис. 1.7 , функции в узлах,
кратных t,
обращаются в 0 все, кроме одной, для
которой t0
= kt.
Это означает, что в данных точках ряд
(1.118) в узлах вырождается в один член, то
есть, в этих точках значения непрерывного
сигнала представляются рядом (1.118)
абсолютно точно.
В прямом выражении ряд (1.118) не может быть применим, так как необходимы сведения о бесконечном числе точек отсчёта, в том числе о тех отсчётах, которые к данному моменту не наступили. С другой стороны, функции, с помощью которых восстанавливается непрерывное колебание, физически нереализуемы, поскольку представляют собой переходные характеристики идеального фильтра нижних частот (фильтра с П-образной АЧХ). Независимо от этого, свойство представления колебания рядом дискретных отсчётов используется на практике, только формула (1.117) модифицируется:
|
|
(1.119) |
где m>1 - коэффициент запаса, зависящий от способа представления отсчётов и характера восстановления непрерывного колебания.
Процедура представления непрерывного колебания рядом отсчётов называется дискретизацией. Чаще всего на практике используется равномерная дискретизация, при которой t=const. Случаи неравномерной дискретизации будут рассмотрены ниже.
Если возможный диапазон изменения u(t) разбить на конечное множество областей (квантов) с шагом u, а значение u(t) представлять по принципу принадлежности к определённой области, такая процедура называется квантованием. При этом физическую величину заменяют условной записью принадлежности к определённому кванту. В простейшем случае эту функцию выполняют аналого-цифровые преобразователи (АЦП), в которых признак принадлежности к определённому кванту представляется двоичным кодом.
П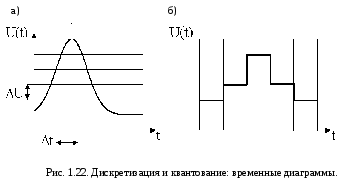 риведём
пример. Предположим, проводится
процедура квантования напряжения в
диапазоне (0-1) В, и число разрядов АЦП
выбрано равным 8. При 8-разрядном двоичном
коде можно закодировать 28
= 256 различных квантов (уровней).
Абсолютная величина одного кванта в
этом случае равна (1/256)0.004В,
что определяет погрешность квантования
в 0.4%. Тогда, например, амплитуда =0.37В
будет представлена кодом 01001010. В
принципе этот код можно представить
символом в коде ASCII, что не изменяет
точности измерения.
риведём
пример. Предположим, проводится
процедура квантования напряжения в
диапазоне (0-1) В, и число разрядов АЦП
выбрано равным 8. При 8-разрядном двоичном
коде можно закодировать 28
= 256 различных квантов (уровней).
Абсолютная величина одного кванта в
этом случае равна (1/256)0.004В,
что определяет погрешность квантования
в 0.4%. Тогда, например, амплитуда =0.37В
будет представлена кодом 01001010. В
принципе этот код можно представить
символом в коде ASCII, что не изменяет
точности измерения.
Процедуры дискретизации и квантования можно представить в виде временных диаграмм, что представленно на рис. 1.22.
Случаи нелинейного квантования в принципе используются [28], но практически используются редко в связи с большим распространением линейных АЦП, в том числе в интегральном исполнении.
