Остаточной дисперсией называется величина

(11)

В знаменателе остаточной дисперсии стоит число степеней свободы равное (n – 2), а не n, так как две степени свободы теряются при определении двух параметров (a, b).

Далее вычислим значения математических ожиданий и дисперсий для коэффициентов а и b. Для коэффициента a мы имеем:

(12)

Для коэффициента b получаем:

(13)

Подставив в выражения теоретических дисперсий параметров a и b вместо σ² ее оценку S², получим оценки дисперсий этих параметров:

, (14)

. (15)

Для проверки значимости коэффициентов a и b вычислим статистики:

, , (16)

здесь S_a, S_b - стандартные ошибки коэффициентов регрессии т. е.

; .

Статистики t_a и t_b подчиняются распределению Стьюдента с числом степени свободы v = n – 2. Выдвинем гипотезу Н₀: a = 0 и для заданного уровня значимости α (обычно α = 0,05) и числа степеней свободы v = n – 2 найдем из таблицы распределения критерия Стьюдента критическое значение t_кр = t(α,v).

Если t_a > t_кр гипотезу Н₀ отвергаем и считаем коэффициент а значимо отличным от нуля.

Если t_a > t_кр у нас нет оснований отвергать гипотезу Н₀ т. е. в этом случае считаем, что коэффициент а не значимо отличается от нуля.

Аналогично производится проверка на значимость и коэффициента b.

Выборочный коэффициент парной корреляции между переменными x и y определяемый по выборке из n наблюдений вычисляется по формуле: (17)

Более удобным для практических расчетов значений r_xy является формула: (18)

Выборочный коэффициент парной корреляции дает количественную оценку тесноты линейной связи между переменными x и y. Он является безразмерной величиной и изменяется в диапазоне -1 ≤ r_xy ≤ 1. Если r_xy = 1, это означает, что между переменными x и y существует прямо пропорциональная линейная функциональная зависимость, если r_xy = -1 это означает, что между переменными x и y существует обратно пропорциональная линейная функциональная зависимость. Если r_xy = 0, то это означает, что между переменными x и y линейной зависимости нет (хотя нелинейная зависимость может существовать), в этом случае говорят, что переменные x и y некоррелированы. В случае, когда -1 < r_xy < 1, говорят что переменные x и y стохастически (вероятностно) линейно связаны. Значимость этой зависимости проверяется следующим образом: вычисляется статистика:

(19)

Статистика t_r подчиняется распределению Стьюдента с числом степени свободы v = n – 2. Выдвигается нулевая гипотеза Н₀: ρ_xy = 0. Далее для заданного уровня значимости α и числа степени свободы v = n – 2 по таблице распределения критерия Стьюдента находим t_кр = t(α, v).

Если |t_r| > t_кр, то нулевая гипотеза об отсутствии линейной зависимости между переменными x и y отвергается, в этом случае переменные x и y считаются коррелированными.

Если |t_r| < t_кр, то у нас нет оснований для того, чтобы отвергнуть нулевую гипотезу, в этом случае мы должны признать, что между переменными x и y не существует значимой линейной зависимости т. е. они не коррелированы.

Теперь покажем, что проверка на значимость выборочного коэффициента парной корреляции r_xy и коэффициента детерминации R² эквивалентны. С одной стороны:

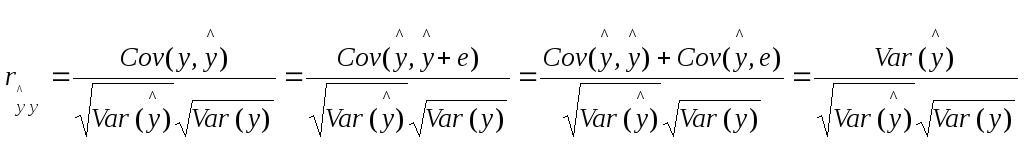
(20)

с другой стороны

(21)

Из формул (20) и (21) следует, что

(22)

Из формулы (22) следует, что t_r = из чего делаем вывод о том, что проверка на значимость выборочного коэффициента парной корреляции r_xy и коэффициента детерминации R² эквивалентны.

Наблюдаемые значения объясняемой переменной y_i () отличаются от прогнозируемых значений , рассчитанных по уравнению регрессии. Чем меньше эти отличия, тем ближе прогнозируемые значения подходят к наблюдаемым значениям y_i, и тем лучше качество построенной модели. Величина отклонения наблюдаемого и прогнозируемого значения объясняемой переменной по каждому наблюдению представляет собой ошибку аппроксимации. Так как может быть как величиной положительной, так и отрицательной, то ошибку аппроксимации для каждого наблюдения принято определять в процентах и по модулю.

Выражение можно рассматривать как абсолютную ошибку аппроксимации, а выражение:

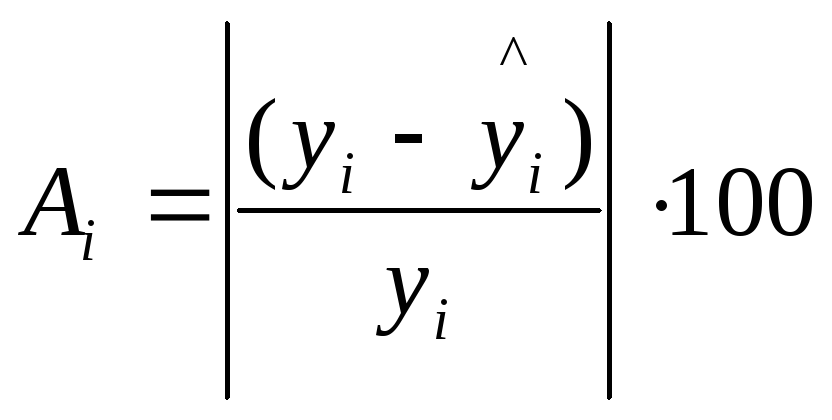
как относительную ошибку аппроксимации для i-го наблюдения.

Чтобы иметь показатель, характеризующий качество модели в целом, определяют среднюю ошибку аппроксимации по всем наблюдениям в выборке по формуле:

.

Считается [2, 3], что построенное уравнение регрессии достаточно хорошо прогнозирует наблюдаемые значения объясняемой переменной, если .

В прогнозных расчетах по построенному уравнению регрессии (2) определяется предсказываемое значение, как точечный прогноз при x = x_p, т. е. путем подстановки в уравнение регрессии (2) соответствующего значения объясняющей переменной x. Однако надо признать, что точечный прогноз явно не реален. Поэтому он дополняется расчетом стандартной ошибки т.е. и соответственно интервальной оценкой наблюдаемых значений.

Ошибка предсказания равна разности между предсказанным и действительным значениями:

.

Ошибка предсказания имеет нулевое математическое значение:

Вычислим дисперсию прогноза, поскольку

то для дисперсии прогноза имеем

Из этой формулы следует, что чем больше x_p отклоняется от выборочного среднего , тем больше дисперсия ошибки предсказания, и чем больше объем выборки n, тем меньше дисперсия.

Заменяя в дисперсии прогноза на ее оценку S² и извлекая квадратный корень, получим стандартную ошибку предсказания

.

Доверительный интервал для действительного значения y_p определяется выражением:

,

где t_кр – критическое значение t – статистики при заданном уровне значимости и соответствующем объему выборки числе степеней свободы.

На Рис. 1 отрезок отмеченный стрелками определяет доверительный интервал истинного значения объясняемой переменной y_p относительно предсказанного по уравнению регрессии значения .

Рис. 1

Теперь рассмотрим на конкретном примере, как применяется на практике изложенная выше теория парного линейного регрессионного анализа.

В качестве примера рассмотрим зависимость между сменной добычей торфа на одного рабочего y(т) и мощностью пласта x(м) по следующим (условным) данным, характеризующим процесс добычи торфа в n = 10 карьерах.

Таблица 1

I	1	2	3	4	5	6	7	8	9	10
xi	4	11	14	9	8	8	15	9	8	12
yi	2	8	10	6	4	5	12	4	5	9

Для определения вида зависимости между x и y построим корреляционное поле ( смотрите Рис. 2 ):

Рис. 2

По расположению точек на корреляционном поле полагаем, что зависимость между x и y линейная: y = a + bּx.

По формулам, приведенным ранее, находим:

;

;

;

;

;

;

;

;

;

;

;

;

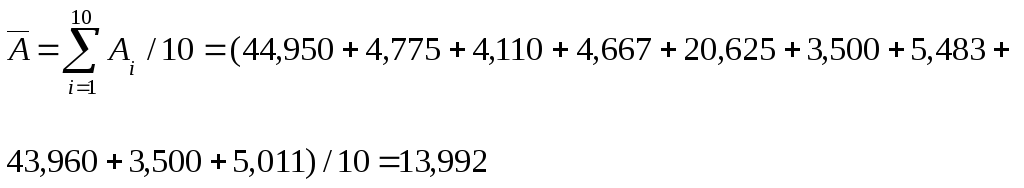
Для повышения наглядности вычислений по МНК построим таблицу 2:

Таблица 2

№	xi	yi	x2i	xiּyi	y2i					Аi
1	4	2	16	8	4	1.100	20.250	29.155	0.809	44.950
2	11	8	121	88	64	7.617	2.250	1.248	0.147	4.775
3	14	10	196	140	100	10.410	12.250	15.288	0.168	4.110
4	9	6	81	54	36	5.755	0.250	0.555	0.066	4.667
5	8	4	64	32	16	4.824	6.25	2.808	0.679	20.625
6	8	5	64	40	25	4.824	2.25	2.808	0.031	3.500
7	15	12	225	180	144	11.341	30.25	23.435	0.424	5.483
8	9	4	81	36	16	5.755	6.25	0.555	3.081	43.900
9	8	5	64	40	25	4.824	2.25	2.808	0.031	3.500
10	12	9	144	108	81	8.548	6.25	4.195	0.204	5.011
∑	98	65	1056	726	511	65	88.50	82.856	5.044	139.92
среднее	9.8	6.5	105.6	72.6	51.1	6.5	8.85	8.286	0.564	13.992

Теперь определим значимость параметров a = -2.623 и b = 0,931, входящих в построенное уравнение регрессии. Для этого зададимся уровнем значимости α = 0,05; вычислим число степеней свободы v = n – 2 = 10 – 2 = 8. И далее по таблице распределения критерия Стьюдента определим t_кр = t(α,v₁) = t(0,05; 8) = 2,301. Так как t_a = 2,972 > t_кр = 2,301 и t_b = 10.837 > t_кр = 2,301 оба параметра значимо отличаются от нуля и должны быть оставлены в модели. Значит, построенное уравнение регрессии будет иметь вид:

(23)

Теперь определим, насколько хорошо построенное уравнение регрессии описывает наблюдаемые значения y. Для этого снова зададимся уровнем значимости α = 0,05; найдем по формулам: k₁ = 1, k₂ = n – 2 = 10 – 2 = 8 числа степеней свободы; далее по таблице распределения критерия Фишера - Снедекора найдем F_кр = F(α, k_1, k₂) = F(0,05;1;8) = 5,320. Так как F = 117,000 > F_кр = 5,320; то делаем вывод, что построенное уравнение регрессии адекватно описывает наблюдаемые значения переменной y и им можно пользоваться для прогнозирования значений y при соответствующих значениях x.

Для построенной модели значение коэффициента детерминации R² = 0,936; что свидетельствует о том, что 93,6% вариации значений переменной y объясняется изменчивостью переменной x, и только 6,4% вариации значений y объясняется воздействием случайного фактора.

Для построенной модели значение выборочного коэффициента корреляции есть r_xy = 0,968. По формуле (19) вычислим значение . (24)

Выдвинем гипотезу Н₀: ρ_xy = 0. Зададимся уровнем значимости α = 0,05, вычислим v = n – 2= 10 – 2 = 8 и по таблице распределения критерия Стьюдента найдем t_кр = 2,310.

Для t_кр и t_r выполняется неравенство t_r = 10.823 > t_кр = 2,301 из которого мы делаем вывод, что нулевая гипотеза должна быть отвергнута и мы должны признать, что между переменными x и y существует значимая линейная зависимость. Это является еще одним подтверждением адекватности построенного уравнения регрессии (23).