
- •1.Проектирование сборного балочного междуэтажного перекрытия
- •1.1 Компоновка конструктивной схемы сборного перекрытия
- •1.2. Расчёт и конструирование многопустотной предварительно-напряжённой плиты перекрытия при временной нагрузке 10000 н/м2 .
- •1.2.1 Исходные данные
- •Материалы для плиты:
- •1.2.2 Расчёт плиты по предельным состояниям первой группы. Определение внутренних усилий
- •Расчёт по прочности сечения, нормального к продольной оси плиты
- •Расчёт по прочности сечения, наклонного к продольной оси плиты
- •1.2.3 Расчёт плиты по предельным состояниям второй группы Геометрические характеристики приведённого сечения
- •Потери предварительного напряжения арматуры
- •Расчёт по образованию трещин, нормальных к продольной оси
- •Расчёт по раскрытию трещин, нормальных к продольной оси
- •Расчет прогиба плиты
- •2 Расчёт и конструирование однопролётного ригеля
- •2.1 Исходные данные
- •2.2 Определение усилий в ригеле
- •2.3 Расчёт прочности ригеля по сечению, нормальному к продольной оси
- •2.4 Расчёт прочности ригеля по сечению, наклонному к продольной оси
- •2.5 Построение эпюры материалов
- •3. Расчёт и конструирование колонны
- •3.1 Исходные данные
- •Материалы для колонны:
- •3.2 Определение усилий в колонне
- •3.3 Расчёт прочности колонны
- •4 Расчёт и конструирование фундамента под колонну.
- •4.1 Исходные данные
- •4.2 Определение размера стороны подошвы фундамента
- •4.3 Определение высоты фундамента
- •4.4 Расчёт на продавливание
- •4.5 Определение площади арматуры фундамента
- •2. Программные комплексы расчета на эвм. Расчет ригеля
- •6. Список использованной литературы
Расчёт по прочности сечения, наклонного к продольной оси плиты
Расчет прочности наклонных сечений
выполняется согласно п.3.29…3.31. Поперечная
сила
![]() кН.
кН.
Предварительно приопорные участки
плиты заармируем в соответствии с
конструктивными требованиями п.5.27. Для
этого с каждой стороны плиты устанавливаем
по четыре каркаса длиной
![]() с поперечными стержнями 4
В500, шаг которых
с поперечными стержнями 4
В500, шаг которых
![]() см.
(по п.5.27
см.
(по п.5.27
![]() мм).
мм).
Проверяем условие обеспечения прочности по наклонной полосе между наклонными трещинами по формуле:
![]() ,
где
,
где
![]() -
коэффициент, учитывающий влияние
хомутов, нормальных к продольной оси
элемента;
-
коэффициент, учитывающий влияние
хомутов, нормальных к продольной оси
элемента;
![]() -
коэффициент, учитывающий класс и вид
бетона.
-
коэффициент, учитывающий класс и вид
бетона.
![]()
![]() 1,3;
где
1,3;
где
![]() и
и
![]() .
.
![]() ;
;
При
![]() см2
(44 В500) коэффициент
поперечного армирования
см2
(44 В500) коэффициент
поперечного армирования
![]() .
.
Отсюда
![]() .
.
Коэффициент
![]() ,
где
,
где
![]() для
тяжелого бетона.
для
тяжелого бетона.
Делаем проверку:
![]() ;
;
![]() .
.
Условие выполняется.
Следовательно, размеры поперечного сечения плиты достаточны для восприятия нагрузки.
Проверяем необходимость постановки расчетной поперечной арматуры исходя из условия:
![]() ,
где
,
где
![]() -
коэффициент, принимаемый для тяжелого
бетона.
-
коэффициент, принимаемый для тяжелого
бетона.
Коэффициент, учитывающий влияние сжатых полок в двутавровых элементах, равен:
![]() ;
;
При этом принимается, что
![]() .
С учетом этого получаем:
.
С учетом этого получаем:
![]() .
.
Коэффициент, учитывающий влияние
продольной силы обжатия
![]() равен:
равен:
![]() ,
,
где![]() -(значение
силы обжатия
-(значение
силы обжатия
![]() см. ниже) принимается с учетом коэффициента
см. ниже) принимается с учетом коэффициента
![]() :
:
![]() ;
;
Принимаем
![]() .
Тогда
.
Тогда
![]() .
.
Принимаем
![]() .
.
![]()
Условие выполняется.
Вывод: Поперечная арматура ставится по конструктивным требованиям.
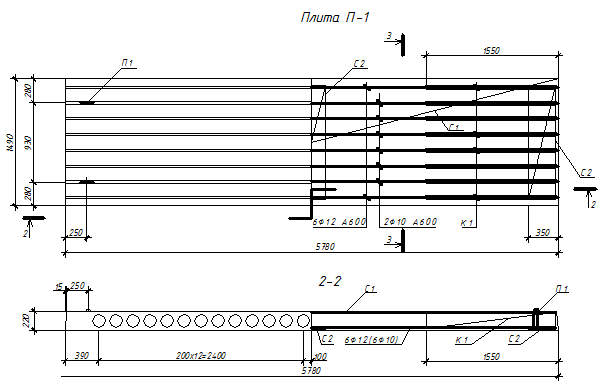
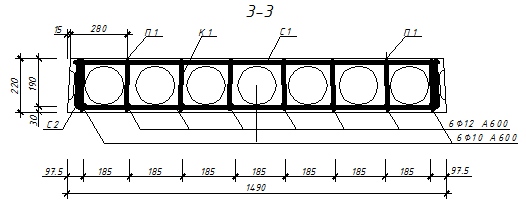
Рисунок 3. Опалубка плиты П-1 и схема армирования
1.2.3 Расчёт плиты по предельным состояниям второй группы Геометрические характеристики приведённого сечения
Определим напряжения в сечении
предварительно напряженного железобетонного
элемента в стадии до образования трещин.
Рассмотрим приведенное бетонное сечение
с геометрическими характеристиками,
в котором круглое очертание пустот
заменим эквивалентным квадратным со
стороной
![]() см.,
в котором площадь сечения арматуры
заменим эквивалентной площадью бетона.
Размеры расчетного двутаврового
сечения:
см.,
в котором площадь сечения арматуры
заменим эквивалентной площадью бетона.
Размеры расчетного двутаврового
сечения:
-толщина полок
![]() см;
см;
-ширина ребра
![]() см;
см;
-ширина полок
![]() см,
см,
![]() см.
см.
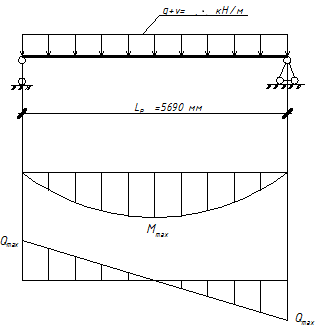
Рисунок 4. Расчетная схема плиты и эпюры усилий
Исходя из равенства деформаций арматуры
и бетона, приведение выполним по отношению
модулей двух материалов
![]() ,
,
Площадь приведенного сечения составит:
![]()
Статический момент приведенного сечения относительно нижней грани равен:
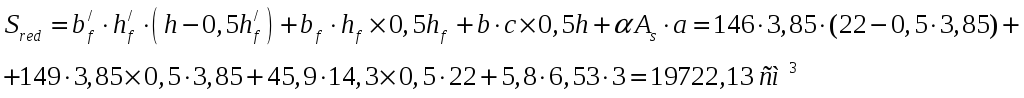
Расстояние от нижней грани до центра тяжести приведенного сечения равно:
![]() см.
см.
Момент инерции приведенного сечения относительно его центра тяжести равен:
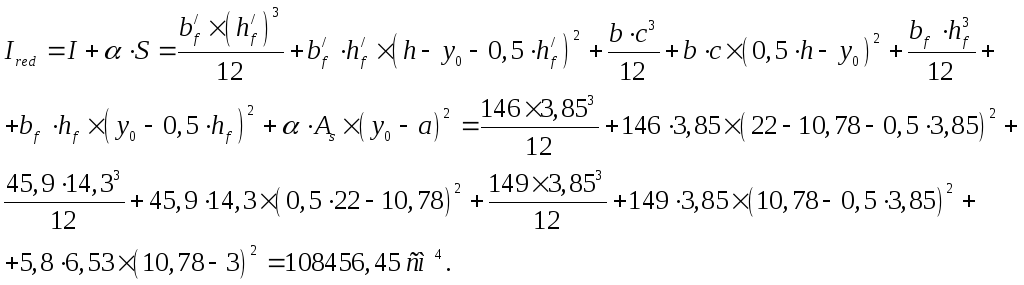
Момент сопротивления приведенного сечения по нижней зоне равен:
![]() см3;
см3;
то же, по верхней зоне:
![]() см3.
см3.
Расстояние от центра тяжести приведенного сечения до ядровой точки, наиболее удаленной от растянутой зоны, согласно формуле:
![]() .
.
Максимальное напряжение в сжатом
бетоне от внешней нагрузки и усилия
предварительного напряжения составит:
![]() ,
где
,
где
![]() -
изгибающий момент от полной нормативной
нагрузки, равный 79770 (Нм);
-
изгибающий момент от полной нормативной
нагрузки, равный 79770 (Нм);
![]() -
усилие обжатия с учетом всех потерь
-
усилие обжатия с учетом всех потерь
![]() (см. расчет потерь),
(см. расчет потерь),
![]() Н.
Н.
Эксцентриситет усилия обжатия равен:
![]() см.
см.
![]()
![]() принимаем
принимаем
![]() .
.
![]() см.
см.
Расстояние от центра тяжести приведенного сечения до ядровой точки, наименее удаленной от растянутой зоны, составляет:
![]() см.
см.
Упругопластический момент сопротивления по растянутой зоне, определяемый по формуле:
![]() .
.
Для симметричных двутавровых сечений
при
![]() .
.
Тогда
![]() см3;
см3;
![]() см3.
см3.
