§4. Критерий устойчивости Михайлова

Рассмотрим левую часть характеристического уравнения (11), которая

представляет собой характеристический полином:

D(S) =a₀sⁿ+a₁ s^n-3 +...+a_n-1s + a_n. (l6)

Заменим в этом полиноме s = ω, где ω представляет собой угловую частоту

колебаний, соответствующих чисто мнимому корню характеристического

уравнения. При этом получим характеристический вектор

D(jω) =а₀(Jω)ⁿ + а₁(Jω)^n-1 +... + a_n-1 Jω + а_п =ReD(jω) + JmD(jω) = X(ω) + jY(ω) (17)

где вещественная часть будет содержать четные степени ω: X(ω) = ReD(jω) = a_n-a_n-₂aω²+... (18)

а мнимая - нечетные степени ω:

Y(ω) = JmD(jω) = а _{n - 1} ω – а_{n - 2}ω³ +... (19)

Из формулы (15) следует формулировка критерия устойчивости Михайлова. Система автоматического управления устойчива, если при

изменении частоты ω от 0 до ∞ вектор D(j ω) поворачивается на угол степень характеристического уравнения D(s)=0.

Вектор D(jco) при изменении частоты от нуля до ∞ (0 < ω <∞) вычертит в плоскости комплексного переменного некоторую кривую (годогфаф), которая

называется кривой Михайлова.

Тогда критерий Михайлова можно сформулировать: система устойчива, если годограф D(jco) с ростом частоты от нуля до ор, начинаясь на действительной оси, обходит последовательно в положительном направлении (против часовой стрелки) п квадрантов.

Практически годограф Михайлова строится по точкам, причем зада­ются различные значения частоты со и по формулам (18) и (19) вычисля­ются Х((й) и Y((o). Результаты расчетов сводятся в таблицу, по которой и строится годограф.

Оказывается, что годограф Михайлова для устойчивых систем всегда имеет плавную спиралевидную форму, причем конец его уходит в бесконечность в том квадранте комплексной плоскости, номер которого равен степени характеристического полинома (рис.4).

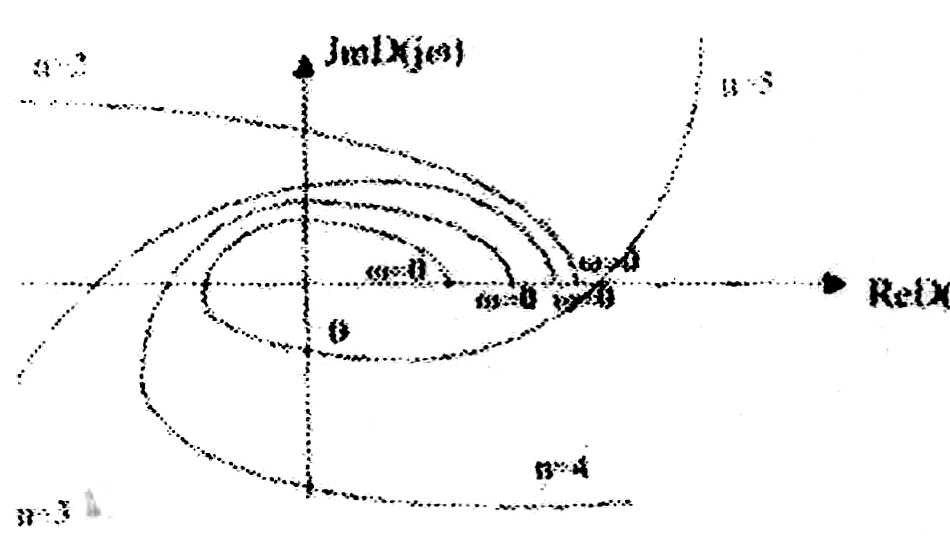
Рис.4. Частотный годограф Михайлова для устойчивых систем порядка п. Неустойчивость системы всегда связана с тем, что в годографе Михайлова нарушается последовательность прохождения квадрантов, вследствие чего

угол поворота вектора D(jω) оказывается меньшим, чем п*π/2

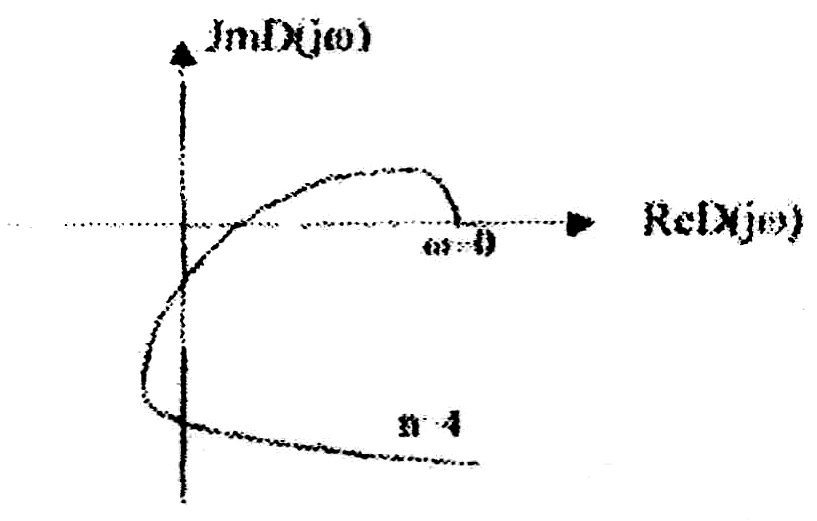
Рис.5. Частотный годограф Михайлова для неустойчивых систем четвертого порядка.

Наличие границы устойчивости всех трех типов рассмотрим на примере

системы четвертого порядка

В случае границы устойчивости первого типа (нулевой корень) отсутствует свободный член характеристического полинома а_п-0, т.е. а₄=0 и кривая Михайлова идет из начала координат (рис 6,а).

При границе устойчивости второго типа (колебательная граница устойчивости) характеристический полином обращается в нуль при подстановке s = jω₀

D(jω₀)=X(ω₀)+jY(ω₀)=0

откуда вытекают два равенства:

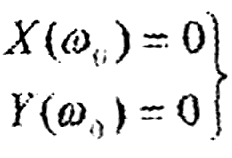
Это значит, что точкаω=ω_о на кривой Михайлова попадает в начало координат (рис.6,6). При этом величина ω_о есть частота незатухающих колебаний.

Для границы устойчивости третьего типа (бесконечный корень) конец годографа Михайлова перебрасывается, как показано на рис.6,в. При этом коэффициент а_о характеристического полинома D(s), будет проходить через нулевое значение, меняя знак плюс на минус.

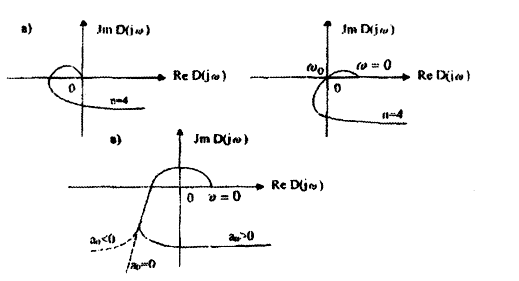
Рис.6. Кривая Михайлова для границ устойчивости первого, второго и третьего типа.