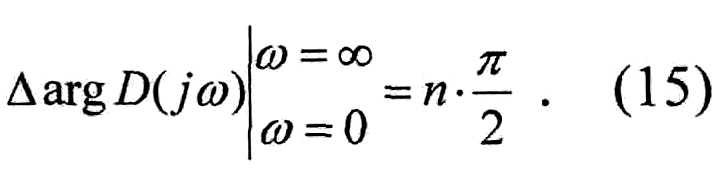§3. Частотные критерии устойчивости

Частотные критерии устойчивости позволяют судить об устойчивости сис­тем автоматического управления по виду их частотных характеристик. Эти кри­терии позволяют сравнительно просто исследовать устойчивость систем высокого порядка, а также имеют геометрическую интерпретацию и наглядность.

Принцип аргумента. Частотные критерии устойчивости динамических сис­тем базируются на принципе аргумента.

Пусть дан некоторый полином n-ой степени D(s)=a₀Sⁿ+a_Is^n-1+...+a_n.(10)

Этот полином представлен в виде произведения сомножителей

D(s)= a₀(s-s₁)(s-s₂)…(s-s_n) (11)

где s₁ s₂ ,. . .,s_n - корни характеристического уравнения D(s)=0.

Характеристический вектор можно тогда представить в следующем виде:

D(jω)=a₀(jω-s₁)(jω-S₂)...(jω-S_n). (12)

Каждая из скобок представляет собой комплексное число. Следовательно, D(jω) представляет собой произведение п комплексных чисел. При перемноже­нии аргументы комплексных чисел складываются. Поэтому результирующий угол поворота вектора D(jω) при изменении частоты о от нуля до бесконечности будет равен сумме углов поворота отдельных сомножителей

(12):

Ψ=ψ₁ +ψ ₂+... + ψ_п. (13)

Условимся считать вращение против часовой стрелки положительным.

Определим каждое слагаемое (13) в отдельности.

1. Пусть какой-либо корень, например s, является вещественным и отрицательным, т.е. S₁ = -α₁ где α₁ >0. Сомножитель в выражении (12), определяемый этим корнем, будет иметь вид (Jω+α₁).

Построим годограф этого вектора на комплексной плоскости при изменении частоты от нуля до бесконечности (рис,2,а). При ω=0 вещественная часть равна a_t, a мнимая нуль. Этому соответствует точка А, лежащая на оси вещественных. При увеличении частоты до бесконечности конец вектора уходит в бесконечность, причем конец вектора все время остается на вертикальной прямой.

Годографы характеристического вектора для S₁ = -a ±jβ,s₂= a±jβ.

При увеличении ω от нуля до бесконечности концы обоих векторов уходят вверх в бесконечность, и оба вектора в пределе сливаются с осью мнимых.

Результирующий угол поворота первого вектора

Результирующий угол поворота второго вектора

Вектор, соответствующий произведению (jω +α - jβ)(jω+α+jβ), повернется на угол

4. Пусть те же комплексные корни имеют положительную вещественную часть, т.е. s_1,2 =+α±jβ. Проводя построения, аналогичные предыдущим (рие.3,6), можно получить, что результирующий угол поворота вектора, соответ­ствующего произведению двух сомножителей, будет

Предположим, что полином D(s) имеет 1 правых корней и (n-1) левых кор­ней.

Получаем следующую формулировку принципа аргумента: изменение (при­ращение) аргумента D(Jω) при изменении частоты со от 0 до со равно разно­сти между числом левых и правых корней уравнения D(s) =0, умноженной на π/2

Для того, чтобы линейная система была устойчива необходимо и достаточно, чтобы все корни характеристического уравнения лежали в левой полуплоскости комплексного переменного s, т.е. чтобы 1=0. В этом случае согласно (14)