Пример оформления на рабочем листе

	B	С
4
5	x=	0,5
6	f(x)=	=C5*TAN(C5)-1

Циклические ссылки

Если в ячейку рабочего листа введена формула, содержащая ссылку на эту же ячейку (может быть и не напрямую, а опосредованно – через цепочку других ссылок), то говорят, что имеет место циклическая ссылка (цикл). Именно вычисление по формулам с циклическими ссылками и использовано в рассматриваемом способе решения нелинейных уравнений. При этом число повторений цикла будет конечным.

Для включения режима циклических вычислений надо выполнить следующие действия:

1. щёлкнуть мышью по кнопке меню Сервис; (2007: Нажмите кнопку Microsoft Office , щелкните Параметры Excel, а затем выберите категорию Формулы.)

2. в раскрывшемся меню щёлкнуть мышью по строке Параметры…;

3. в диалоговом окне Параметры щёлкнуть мышью по вкладке Вычисления;

4. поставить флажок в окне итерации;

5. установить вариант вычислений автоматически;

6. щелкнуть мышью по кнопке ОK.

Уточнение корня уравнения этим способом сводится к следующим действиям.

1. Найти первую производную от функции f(x) из уравнения f(x)=0. В нашем примере производная от функции f(x)=xtg(x)-1 будет иметь вид f ^/(x)=tg(x)+x/cos²(x).

2. В ячейку (например, F5) ввести текст Xнач=.

3. В ячейку ниже (F6) ввести текст x=.

4. В следующую ниже ячейку (F7) ввести текст f(x)=.

5. В ячейку G5 ввести начальное приближение x (число) к искомому корню. В качестве такого приближения можно использовать середину (левую или правую границу) заданного отрезка.

6. В ячейку G6 ввести рекуррентную формулу, задающую вычисление очередного приближения к корню по методу Ньютона 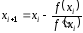. При этом необходимо использовать логическую функцию ЕСЛИ(). Применение этой функции позволит запустить итерационный процесс с начального приближения, записанного в G5. Таким образом, формула, которую надо ввести в ячейку G6, будет иметь вид: =ЕСЛИ(G6=0;G5;G6-(G6*TAN(G6)-1)/ (TAN(G6)+G6/COS(G6)^2)).

7. В ячейку G7 ввести выражение для вычисления значений функции из уравнения. Искомый результат (корень) будет получен в ячейке G6.

Для изменения начального приближения Xнач на другое необходимо выполнить следующие действия.

1. Из ячейки со значением Xнач (G5) удалить прежнее значение и ввести новое.

2. Дважды щёлкнуть мышью (перейти в режим редактирования содержимого) по ячейке с формулой (G6). После чего нажать клавишу Enter. Это приведёт к обнулению прежнего результата и повторному запуску итерационного процесса.

Пример оформления на рабочем листе

	F	G
4
5	Xнач=	0,5
6	x=	=ЕСЛИ(G6=0;G5;G6-(G6*TAN(G6)–1)/ (TAN(G6)+G6/COS(G6)^2))
7	f(x)=	=G6*TAN(G6)-1