5. Формула полной вероятности и формула Байеса

Пусть рассматривается полная группа событий (попарно несовместные, которые называются гипотезами), и если событие может наступить только при появлении одной их этих гипотез, то вероятность события вычисляется по формуле полной вероятности:

,

или

,

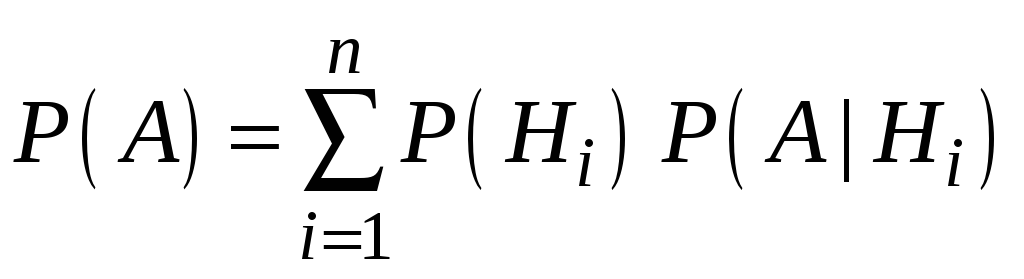где – вероятность гипотезы ..

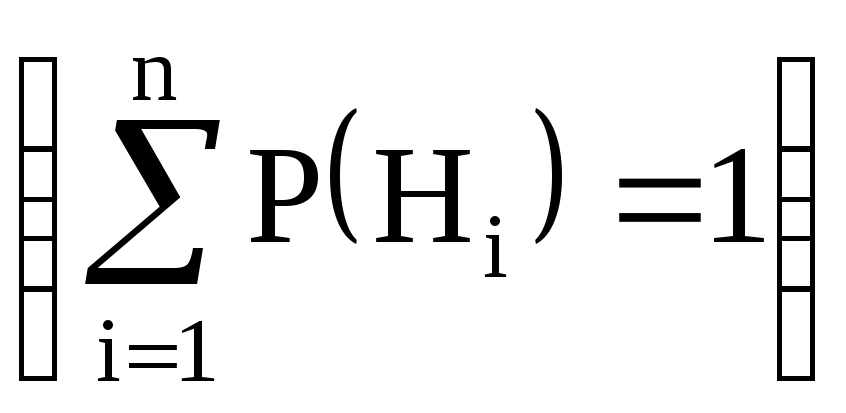– условная вероятность события при этой гипотезе. Если до опыта вероятности гипотез были , а в результате опыта появилось событие , то с учетом этого события «новые», т. е. условные, вероятности гипотез вычисляются по формуле Байеса:

.

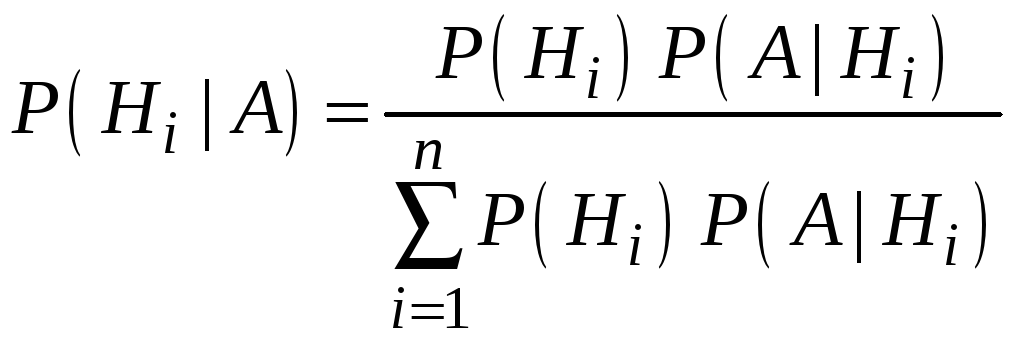Формула Байеса дает возможность переоценить вероятности гипотез с учетом уже известного результата опыта.

Пример 1.

Имеется три одинаковые урны. В первой белых шаров и черных; во второй – белых и черных; в третьей только белые шары. Некто подходит наугад к одной из урн и вынимает из нее шар. Найти вероятность того, что этот шар белый.

Решение.

Пусть событие – появление белого шара. Формулируем гипотезы: – выбор первой урны;

– выбор второй урны;

– выбор третьей урны;

,

, , ;

по формуле полной вероятности

.

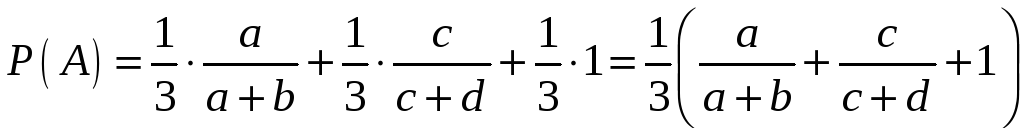Пример 2.

Имеются две урны: в первой белых шаров и черных, во второй – и черных. Из первой урны во вторую перекладывается один шара шар; шары перемешиваются и затем из второй урны в первую перекладывается один шар. После этого из первой урны берут наугад один шар. Найти вероятность того, что он был белым.

Решение.

Гипотезы: – состав шаров в первой урне не изменился;

– в первой урне один черный шар заменен на белый;

– в первой урне один белый шар заменен черным;

;

;

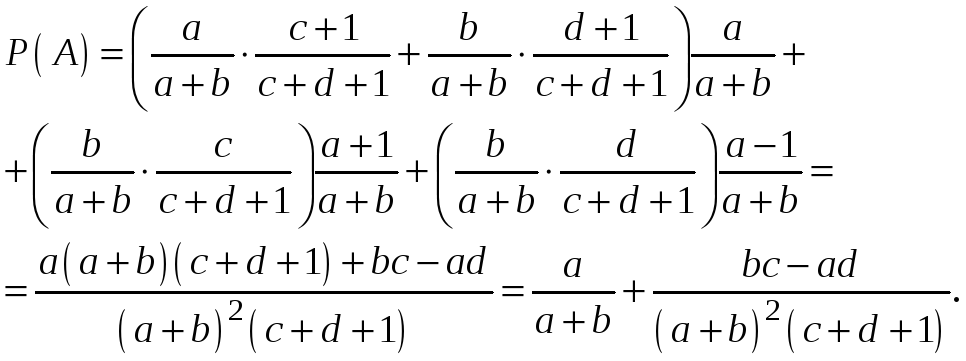
Полученное решение говорит о том, что вероятность вынуть белый шар не изменится, если доли белых шаров и черных шаров в обеих урнах одинаковы .

Ответ: .

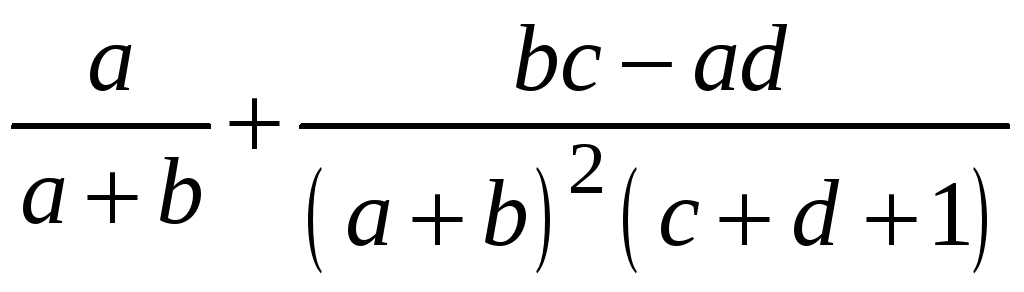Пример 3.

Прибор состоит из двух узлов, работа каждого узла безусловно необходима для работы прибора в целом. Надежность (вероятность безотказной работы в течение времени ) первого узла равна , второго . Прибор испытывается в течение времени , в результате чего обнаружено, что он вышел из строя (отказал). Найти вероятность того, что отказал только первый узел, а второй исправен.

Решение.

До опыта возможны четыре гипотезы:

– оба узла исправны;

– первый узел отказал, второй исправен;

– первый исправен, второй отказал;

– оба узла отказали;

Вероятности гипотез:

Наблюдалось событие – прибор отказал:

По формуле Байеса:

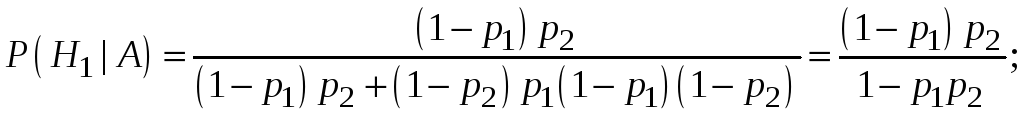
Ответ: .

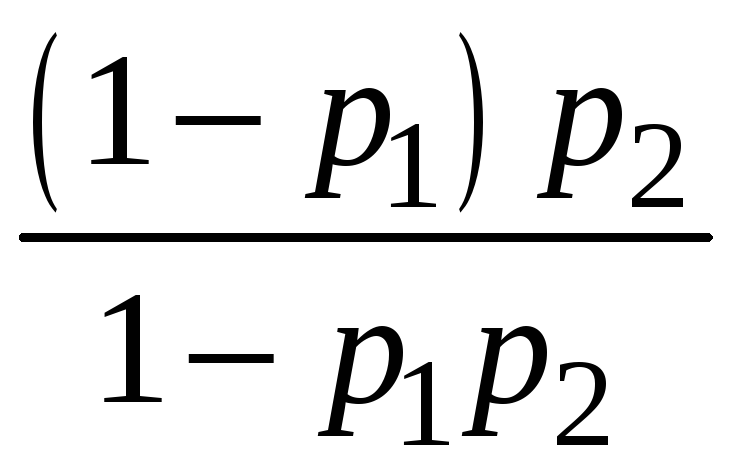6. Повторение опытов

Если производится независимых опытов в одинаковых условиях, причем в каждом из них с вероятностно появляется событие , то вероятность того, что событие произойдет в этих опытах ровно раз, выражается формулой:

,

где .

Вероятность хотя бы одного появления события при независимых опытах в одинаковых условиях равна:

.

Вероятность того, что событие наступит а) менее раз; б) более раз; в) не менее раз; г) не более раз находим соответственно но формулам:

а) ; б) ;

в) ; г) .

Общая теорема о повторении опытов

Если производится независимых опытов в различных условиях, причем вероятность события в -м опыте равна , то вероятность того, что событие появится в этих опытах ровно раз, равна коэффициенту при в разложении по степеням производящей функции

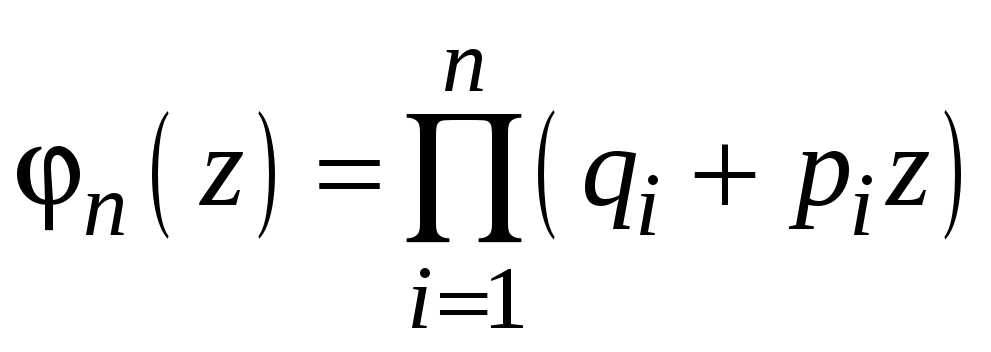, где .

Пример 1.

Прибор состоит г из 10 узлов. Надежность (вероятность безотказной работы в течение времени ) для каждого узла . Узлы выходят из строя независимо один от другого. Найти вероятность того, что за время :

а) откажет хотя бы один узел;

б) откажет ровно один узел;

в) откажут ровно два узла;

г) откажет не менее двух узлов.

Решение.

а) , где

б) ;

в) ;

г) .

Пример 2.

В урне 30 белых и 15 черных шаров. Вынули подряд 5 шаров, причем каждый вынутый шар возвращают в урну перед извлечением следующего и шары в урне перемешивают. Какова вероятность того, что из 5 вынутых шаров окажется 3 белых.

Решение.

Вероятность извлечения белого шара , можно посчитать одной и той же во всех 5 испытаниях: тогда вероятность непоявления белого шара. Используя формулу Бернулли получаем:

.

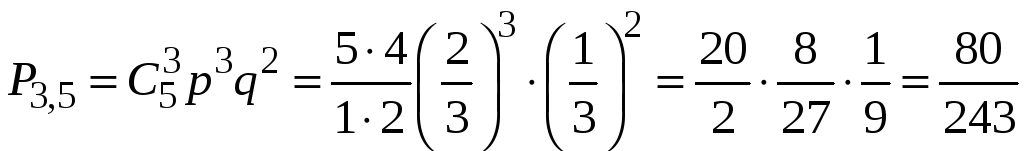Ответ: .

Пример 3.

Монету подбрасывают восемь раз. Какова вероятность того, что шесть раз она упадет гербом вверх?

Решение.

Имеем схемуиспытаний Бернулли. Вероятность появления Ге в одном испытании , тогда

.

Ответ: 0,107.

Пример 4.

Производится четыре независимых выстрела, причем – вероятность попадания в мишень есть средняя из вероятностей

Найти вероятности: .

Решение.

Найдем

По формуле Бернулли имеем

Пример 5.

Имеется пять станций, с которыми поддерживается связь. Время от времени связь прерывается из-за атмосферных помех. Вследствие удаленности станций друг от друга перерыв связи с каждой из них происходит независимо от остальных с вероятностью 0,2. Найти вероятность того, что в данный момент времени будет поддерживаться связь не более чем с двумя станциями.

Решение.

Событие – имеется связь не более чем с двумя станциями.

Ответ: 0,72.

Пример 6.

Система радиолокационных станций ведет наблюдение за группой объектов, состоящей из десяти единиц. Каждый из объектов может быть (независимо от других) потерян с вероятностью 0,1. Найти вероятность того, что хотя бы один из объектов будет потерян.

Решение.

Вероятность потери хотя бы одного объекта можно найти по формуле:

,

но проще воспользоваться вероятностью противоположного события – ни один объект не потерян – и вычесть ее из единицы

.

Ответ: 0,65.