Ентроп́ія

Ентроп́ія S — в термодинаміці міра енергії у термодинамічній системі, яка не може бути використана для виконання роботи. Вона також є мірою безладдя, присутнього в системі.

Поняття ентропії

Поняття ентропії було вперше введено у 1865 році Рудольфом Клаузіусом. Він визначив зміну ентропії термодинамічної системи при оборотному процесі як відношення загальної кількості теплоти ΔQ, отриманої або втраченої системою, до величини абсолютної температури T:

Рудольф Клаузіус дав величині S назву «ентропія», утворивши її від грецького слова τρoπή, «зміна» (зміна, перетворення).

Рівність відноситься саме до зміни ентропії. У термодинаміці ентропія визначається лише з точністю до сталої.

Зв'язок між теплоємністю та ентропією дається формулою

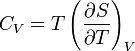
Статистичне визначення ентропії: принцип Больцмана.

У 1877 році, Людвіг Больцман зрозумів зв'язок між ентропією системи та кількістю можливих «мікростанів» (мікроскопічних станів), якими може реалізуватися макроскопічний стан із заданими властивостями. Розглянемо, наприклад, ідеальний газ у посудині. Мікростан визначений як положення та імпульси кожного атома, з яких складається система. Братимемо до уваги тільки ті мікростани, для яких: (i) розташування всіх частинок не виходить за межі посудини, (ii) загальна енергія газу, що визначається як сума кінетичних енергій атомів, дорівнює певній величині. Больцман постулював що

де константа kB=1,38·10-23 Дж/К відома тепер як стала Больцмана, а Ω є числом мікроскопічних станів, можливих у заданому макроскопічному стані. Цей постулат, відомий як принцип Больцмана, може розцінюватися, як початок статистичної механіки, яка описує термодинамічні системи використовуючи статистичну поведінку компонентів, із яких вони складаються. Принцип Больцмана зв'язує мікроскопічні властивості системи (Ω) з однією з її термодинамічних властивостей (S).

Згідно з визначенням Больцмана, ентропія є функцією стану. Більш того, оскільки (Ω) може бути тільки натуральним числом (1,2,3.), ентропія повинна бути додатньою — виходячи з властивостей логарифма.

У випадку дискретних станів квантової механіки підрахунок кількості станів не викликає проблем і проводиться звичайним чином. Складніше підрахувати кількість станів у рамках класичної механіки, в рамках якої мікроскопічний стан системи описується координатами qi й імпульсами pi окремих частинок, що пробігають неперервні значення. Для підрахунку станів у класичних системах фазовий простір розбивають на невеликі комірки із об'ємом, який відповідає зведеній сталій Планка. В такому випадку

,

де s — число незалежних координат, — зведена стала Планка, а інтегрування проводиться по області фазового простору, який відповідає певному макроскопічному стану.

Властивості ентропії

Ентропія є екстенсивною величиною(залежить від маси і об'єму системи), тому сумарна ентропія двох систем

S = S1 + S2

Ентропія є функцією стану системи, її зміна не залежить від способу переходу з кінцевого стану у початковий: ΔS = Sf − Si. В самочинних поцесах, які протікають в ізольованій системі, ентропія зростає(ΔS>0), а в оборотних рівноважних — вона незмінна (ΔS=0).

Ізоентропійність — незмінність ентропії; ізоентропійні п р о ц е с и — зміна стану фізичної системи, коли не змінюється її ентропія.

Третій початок термодинаміки (теорема Нернста)

При абсолютному нулі температури будь-які зміни стану відбуваються без зміни ентропії.

Але абсолютний нуль T = 0 температури недосяжний, тому що інакше був би можливий вічний двигун другого роду η = 1 - = 1.

Для рівноважних систем: при T → 0 ентропія S не залежить від значення будь-якого параметра системи. По 2-му початок термодинаміки:

,

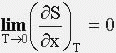Доказ недосяжності абсолютного нуля Т = 0 з 3-го початку термодинаміки:

Охолодження системи здійснюється повторенням послідовно процесів адіабатичного розширення (для зниження Т) і ізотермічного стиснення (для зменшення S). Але при T → 0 ентропія S перестає змінюватися, а набуває деякий постійне значення (прийняте за нуль!). Тому за кінцеве число циклів стан з S = 0 недосяжно, отже, недосяжний і абсолютний нуль температури: до абсолютного нуля температури T → 0 можна лише асимптотично наближатися.