2.4. Сведение матричной игры к задаче линейного программирования

Если матричную -игру нельзя свести к игре или , то её сводят к паре двойственных задач линейного программирования.

Пусть 1) платёжная матрица первого игрока в игре двух игроков, имеющих соответственно и стратегий, имеет вид ;

2) игра не имеет седловой точки в чистых стратегиях;

3) упрощением платёжной матрицы -игру нельзя свести к игре или .

Построим двойственную пару задач линейного программирования для -игры.

Задача линейного программирования для первого игрока. Управляющими переменными ЗЛП для первого игрока будут являться компоненты вектора , удовлетворяющие условиям: и (). Целевая функция для пары задач – это цена игры . Для первого игрока она примет вид .

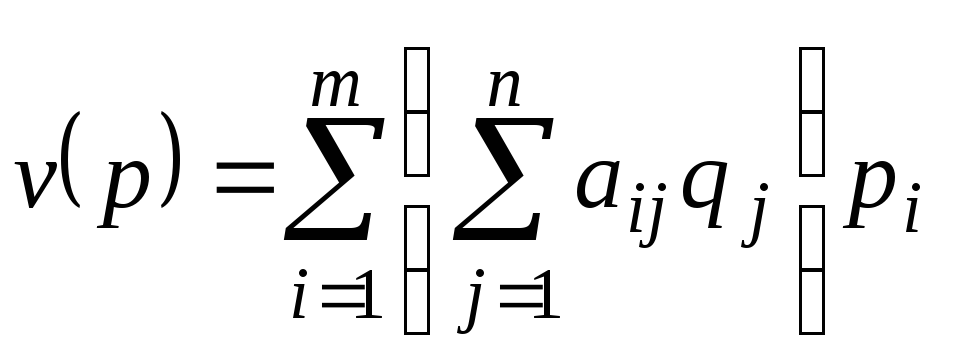Для первого игрока цель игры заключается в максимизации выигрыша, т.е в нахождении такой смешанной стратегии , которая максимизировала бы цену игры первого игрока при любых действиях второго игрока. Поэтому направление оптимизации целевой функции . При этом, согласно теореме 3, применение первым игроком оптимальной стратегии даёт выигрыш, не меньший цены игры, то есть (). Объединяя полученные соотношения в систему, получаем ЗЛП первого игрока:

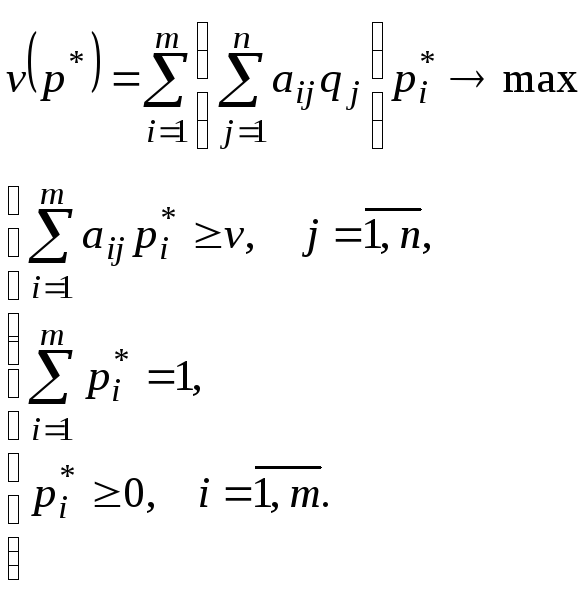
Коэффициентами целевой функции ЗЛП первого игрока являются величины 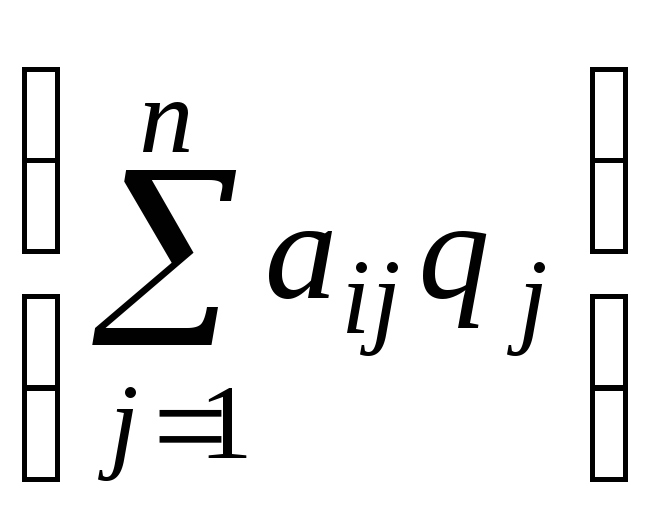, которые меняются в зависимости от поведения второго игрока (меняется вектор ).

Исключим величины 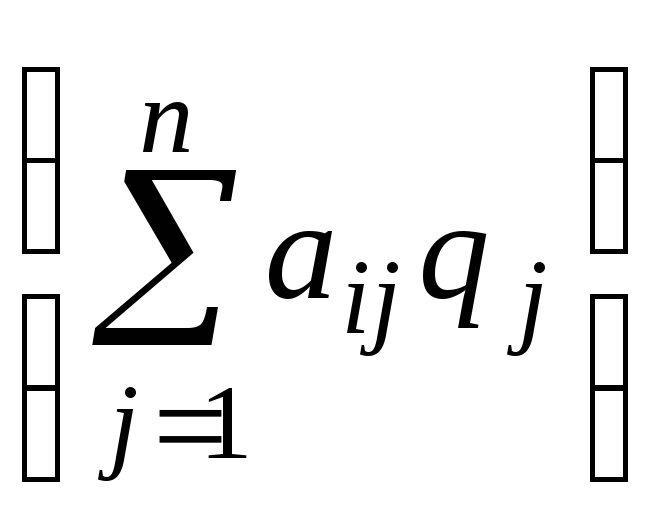из ЗЛП первого игрока. Для этого, предполагая, что , разделим все соотношения системы ограничений на :

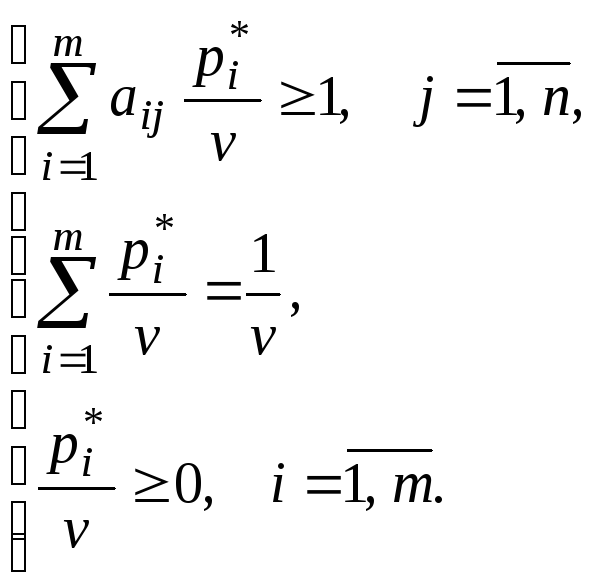
Выполним замену переменных: (). Так как , то . Обозначим тогда ЗЛП первого игрока примет окончательный вид:

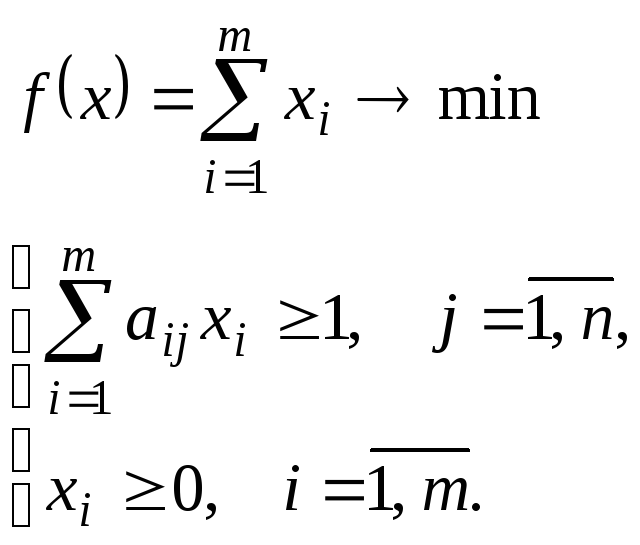
Аналогично строится задача линейного программирования для второго игрока.

Задача линейного программирования для второго игрока. Управляющими переменными ЗЛП для первого игрока будут являться компоненты вектора , удовлетворяющие условиям: и (). Целевая функция для второго игрока примет вид .

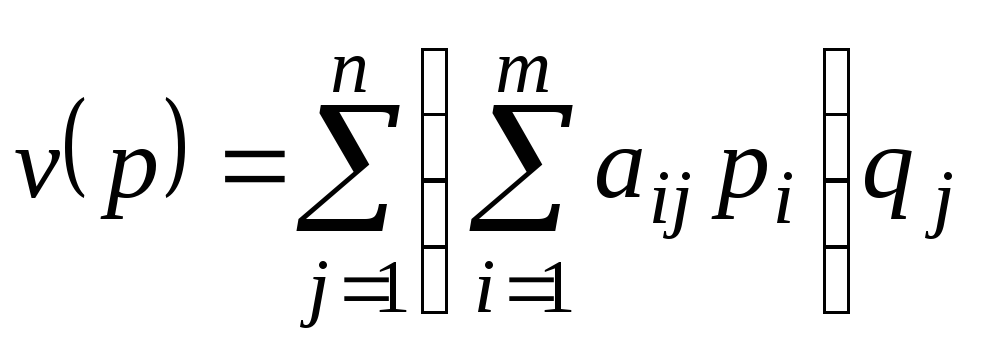Для первого игрока цель игры заключается в минимизации проигрыша, т.е в нахождении такой смешанной стратегии , которая минимизировала бы цену игры первого игрока при любых действиях первого игрока. Поэтому направление оптимизации целевой функции . При этом, согласно теореме 3, применение первым вторым игроком оптимальной стратегии гарантирует проигрыш, не больший цены игры, то есть (). Объединяя полученные соотношения в систему, получаем ЗЛП второго игрока:

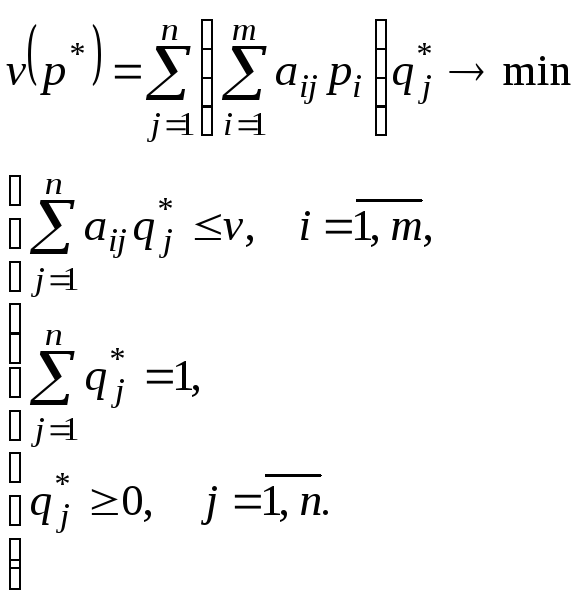
Коэффициентами целевой функции ЗЛП второго игрока являются величины 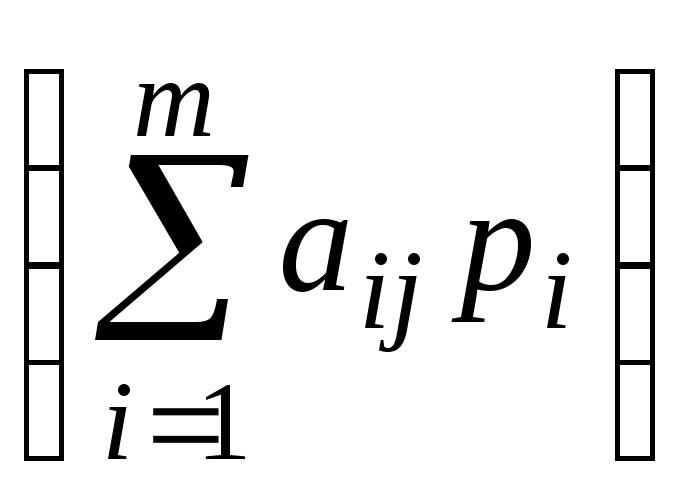, которые меняются в зависимости от поведения первого игрока (меняется вектор ).

Исключим величины 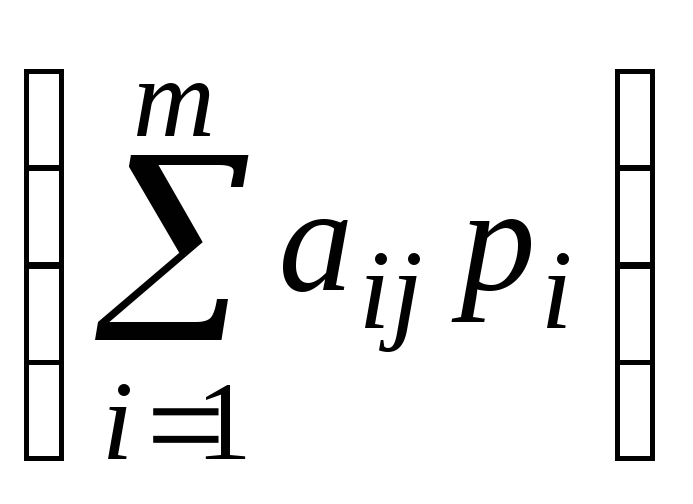из ЗЛП второго игрока. Для этого, предполагая, что , разделим все соотношения системы ограничений на :

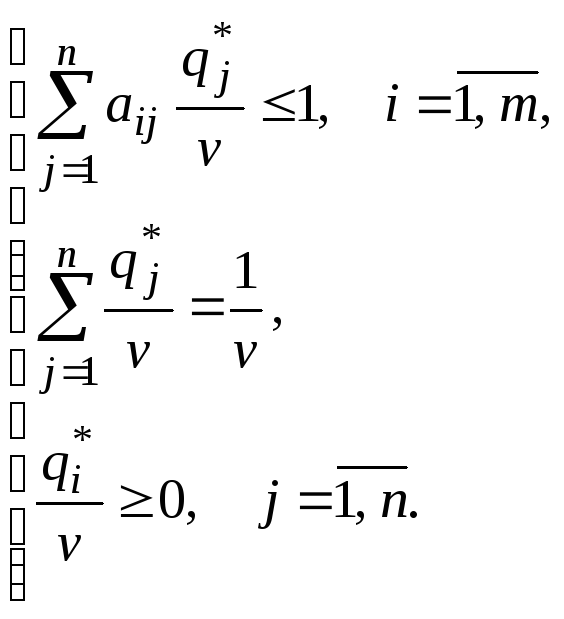
Выполним замену переменных: (). Так как , то . Обозначим тогда ЗЛП второго игрока примет окончательный вид:

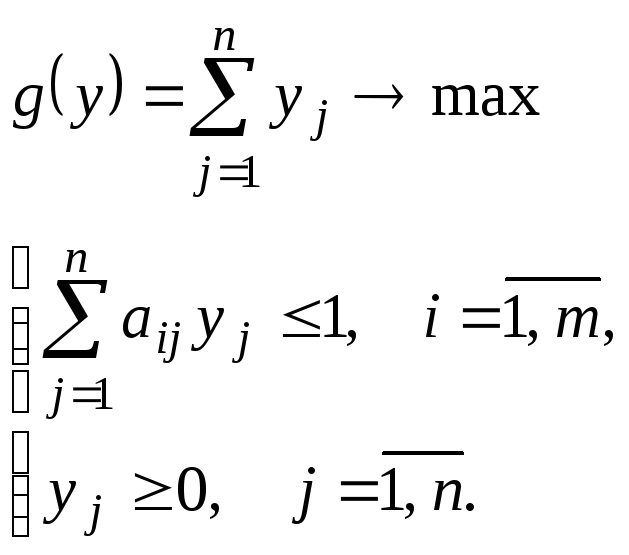
Таким образом, двойственная пара задач линейного программирования для парной -игры с нулевой суммой имеет вид:

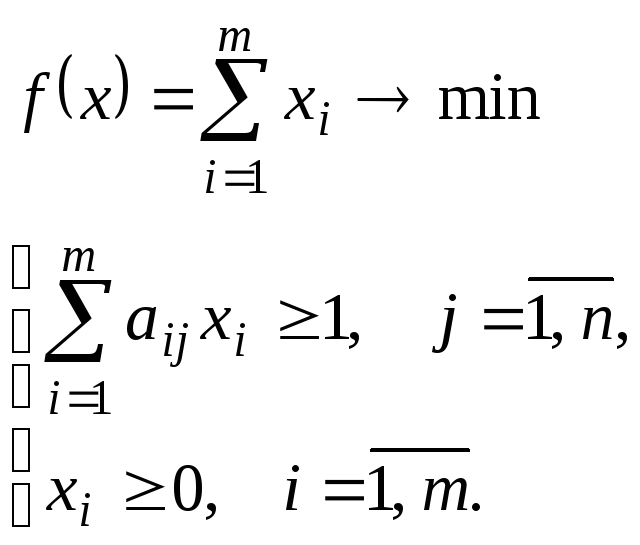
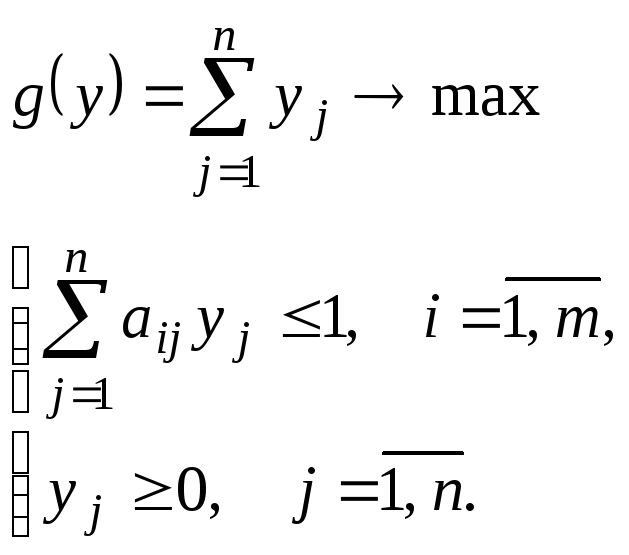
Достаточно решить одну из задач (более удобную), а затем найти решение второй задачи с помощью теорем двойственности (см. тетрадь № 2).

Решение исходно задачи (-игры) находят с помощью обратной замены переменных ( и – решения пары прямой и двойственной задач ЛП):

или , (), ().

Замечание 1. Если в исходной -игре , то игру преобразовывают в соответствии с теоремой 4 в игру с платёжной матрицей , где число . Такое преобразование позволит получить цену преобразованной игры .

Замечание 2. Если в исходной -игре , то при делении на следует менять знак в неравенствах-ограничениях на противоположный.